CACTO-SL: Using Sobolev Learning to improve Continuous Actor-Critic with Trajectory Optimization

Trajectory Optimization (TO) and Reinforcement Learning (RL) are powerful and complementary tools to solve optimal control problems. On the one hand, TO can efficiently compute locally-optimal solutions, but it tends to get stuck in local minima if the problem is not convex. On the other hand, RL is typically less sensitive to non-convexity, but it requires a much higher computational effort. Recently, we have proposed CACTO (Continuous Actor-Critic with Trajectory Optimization), an algorithm that uses TO to guide the exploration of an actor-critic RL algorithm. In turns, the policy encoded by the actor is used to warm-start TO, closing the loop between TO and RL. In this work, we present an extension of CACTO exploiting the idea of Sobolev learning. To make the training of the critic network faster and more data efficient, we enrich it with the gradient of the Value function, computed via a backward pass of the differential dynamic programming algorithm. Our results show that the new algorithm is more efficient than the original CACTO, reducing the number of TO episodes by a factor ranging from 3 to 10, and consequently the computation time. Moreover, we show that CACTO-SL helps TO to find better minima and to produce more consistent results.

CACTO: Continuous Actor-Critic with Trajectory Optimization -- Towards global optimality

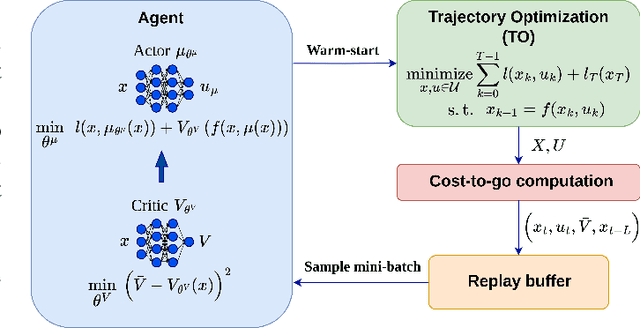
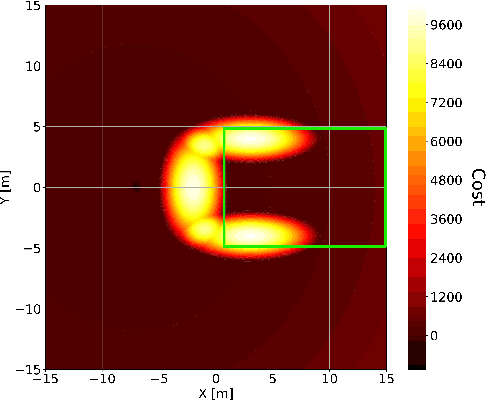
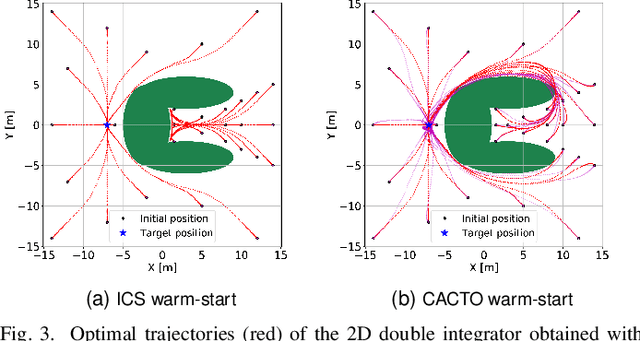
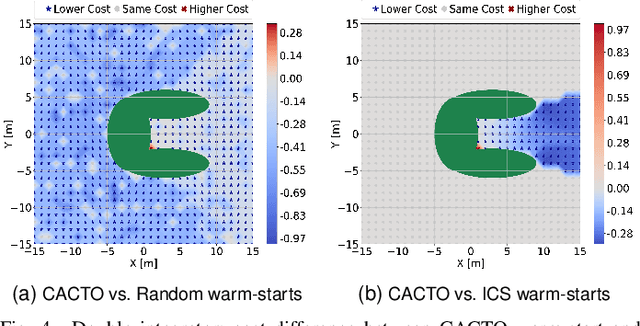
This paper presents a novel algorithm for the continuous control of dynamical systems that combines Trajectory Optimization (TO) and Reinforcement Learning (RL) in a single framework. The motivations behind this algorithm are the two main limitations of TO and RL when applied to continuous nonlinear systems to minimize a non-convex cost function. Specifically, TO can get stuck in poor local minima when the search is not initialized close to a ``good'' minimum. On the other hand, when dealing with continuous state and control spaces, the RL training process may be excessively long and strongly dependent on the exploration strategy. Thus, our algorithm learns a ``good'' control policy via TO-guided RL policy search that, when used as initial guess provider for TO, makes the trajectory optimization process less prone to converge to poor local optima. Our method is validated on several reaching problems featuring non-convex obstacle avoidance with different dynamical systems, including a car model with 6d state, and a 3-joint planar manipulator. Our results show the great capabilities of CACTO in escaping local minima, while being more computationally efficient than the DDPG RL algorithm.