CACTO: Continuous Actor-Critic with Trajectory Optimization -- Towards global optimality
Paper and Code
Nov 12, 2022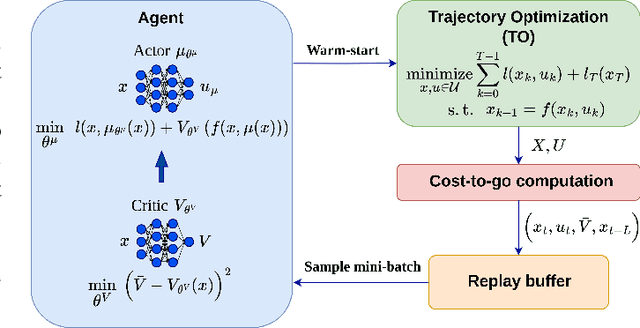
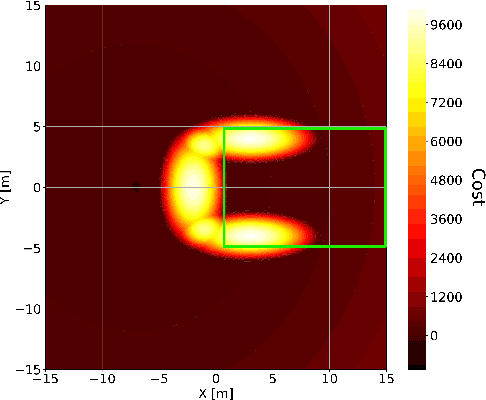
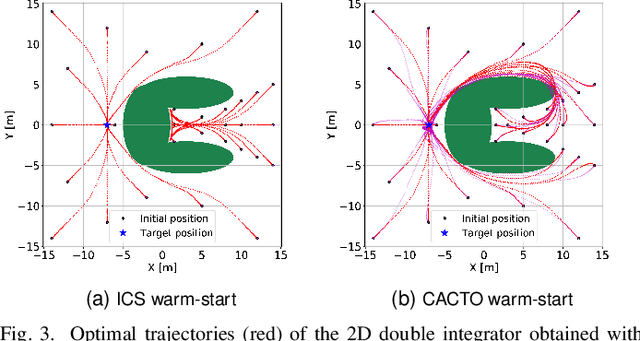
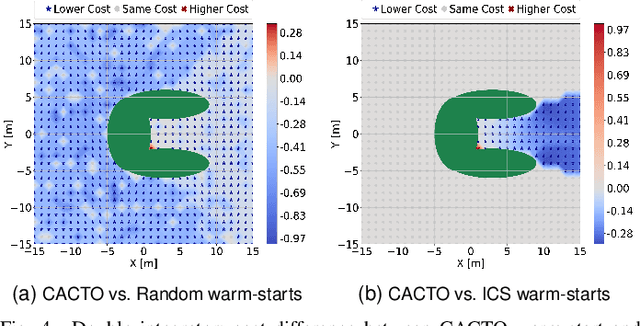
This paper presents a novel algorithm for the continuous control of dynamical systems that combines Trajectory Optimization (TO) and Reinforcement Learning (RL) in a single framework. The motivations behind this algorithm are the two main limitations of TO and RL when applied to continuous nonlinear systems to minimize a non-convex cost function. Specifically, TO can get stuck in poor local minima when the search is not initialized close to a ``good'' minimum. On the other hand, when dealing with continuous state and control spaces, the RL training process may be excessively long and strongly dependent on the exploration strategy. Thus, our algorithm learns a ``good'' control policy via TO-guided RL policy search that, when used as initial guess provider for TO, makes the trajectory optimization process less prone to converge to poor local optima. Our method is validated on several reaching problems featuring non-convex obstacle avoidance with different dynamical systems, including a car model with 6d state, and a 3-joint planar manipulator. Our results show the great capabilities of CACTO in escaping local minima, while being more computationally efficient than the DDPG RL algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge