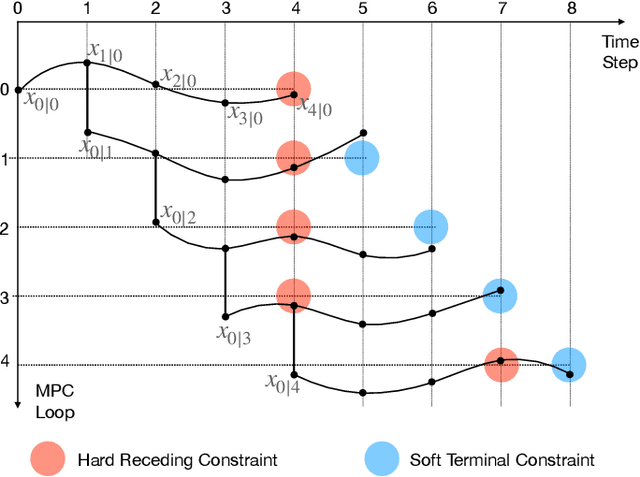
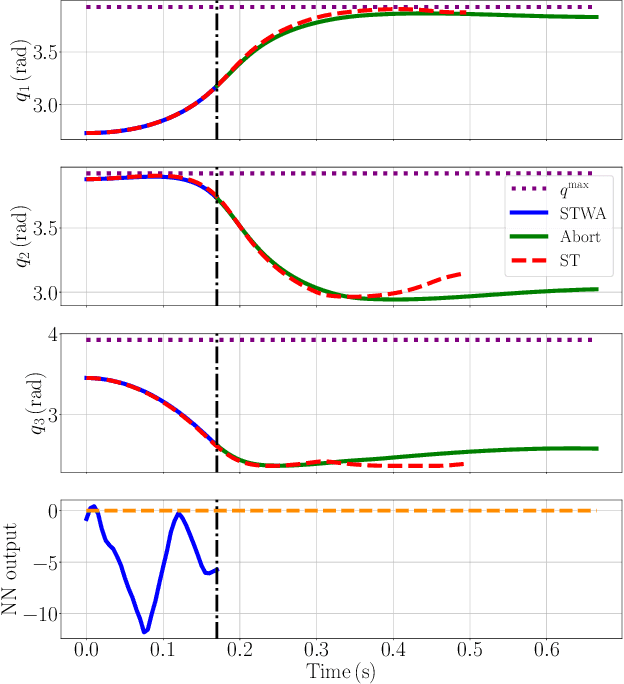
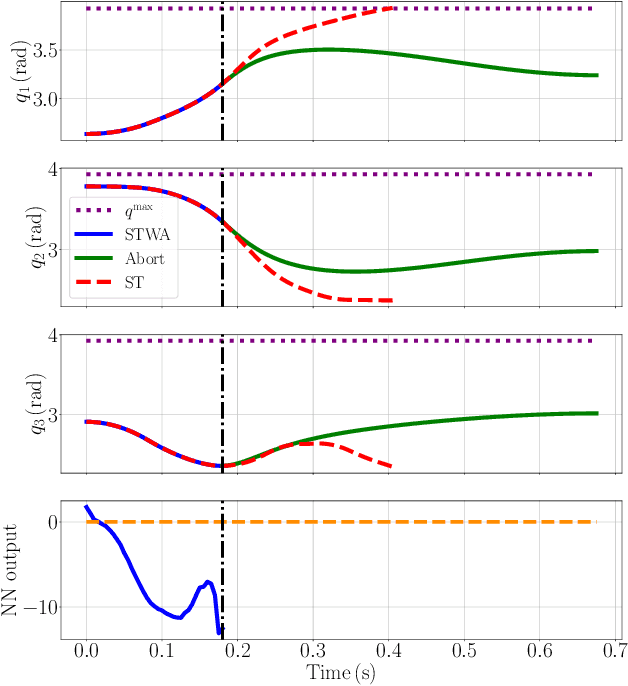
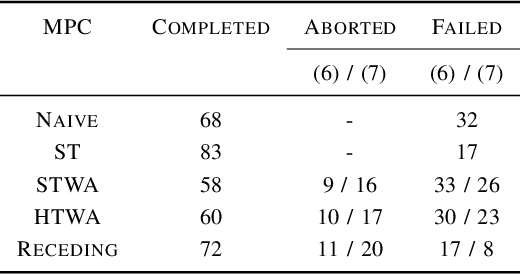
Receding-Constraint Model Predictive Control using a Learned Approximate Control-Invariant Set

In recent years, advanced model-based and data-driven control methods are unlocking the potential of complex robotics systems, and we can expect this trend to continue at an exponential rate in the near future. However, ensuring safety with these advanced control methods remains a challenge. A well-known tool to make controllers (either Model Predictive Controllers or Reinforcement Learning policies) safe, is the so-called control-invariant set (a.k.a. safe set). Unfortunately, for nonlinear systems, such a set cannot be exactly computed in general. Numerical algorithms exist for computing approximate control-invariant sets, but classic theoretic control methods break down if the set is not exact. This paper presents our recent efforts to address this issue. We present a novel Model Predictive Control scheme that can guarantee recursive feasibility and/or safety under weaker assumptions than classic methods. In particular, recursive feasibility is guaranteed by making the safe-set constraint move backward over the horizon, and assuming that such set satisfies a condition that is weaker than control invariance. Safety is instead guaranteed under an even weaker assumption on the safe set, triggering a safe task-abortion strategy whenever a risk of constraint violation is detected. We evaluated our approach on a simulated robot manipulator, empirically demonstrating that it leads to less constraint violations than state-of-the-art approaches, while retaining reasonable performance in terms of tracking cost and number of completed tasks.

VBOC: Learning the Viability Boundary of a Robot Manipulator using Optimal Control

Safety is often the most important requirement in robotics applications. Nonetheless, control techniques that can provide safety guarantees are still extremely rare for nonlinear systems, such as robot manipulators. A well-known tool to ensure safety is the Viability kernel, which is the largest set of states from which safety can be ensured. Unfortunately, computing such a set for a nonlinear system is extremely challenging in general. Several numerical algorithms for approximating it have been proposed in the literature, but they suffer from the curse of dimensionality. This paper presents a new approach for numerically approximating the viability kernel of robot manipulators. Our approach solves optimal control problems to compute states that are guaranteed to be on the boundary of the set. This allows us to learn directly the set boundary, therefore learning in a smaller dimensional space. Compared to the state of the art on systems up to dimension 6, our algorithm resulted to be more than 2 times as accurate for the same computation time, or 6 times as fast to reach the same accuracy.