Motion Accuracy and Computational Effort in QP-based Robot Control

Quadratic Programs (QPs) have become a mature technology for the control of robots of all kinds, including humanoid robots. One aspect has been largely overlooked, however, which is the accuracy with which these QPs should be solved. Typical QP solvers aim at providing solutions accurate up to floating point precision ($\approx10^{-8}$). Considering physical quantities expressed in SI or similar units (meters, radians, etc.), such precision seems completely unrelated to both task requirements and hardware capacity. Typically, humanoid robots never achieve, nor are capable of achieving sub-millimeter precision in manipulation tasks. With this observation in mind, our objectives in this paper are two-fold: first examine how the QP solution accuracy impacts the resulting robot motion accuracy, then evaluate how a reduced solution accuracy requirement can be leveraged to reduce the corresponding computational effort. Numerical experiments with a dynamic simulation of a HRP-4 robot indicate that computational effort can be divided by more than 20 while maintaining the desired motion accuracy.

The hierarchical Newton's method for numerically stable prioritized dynamic control

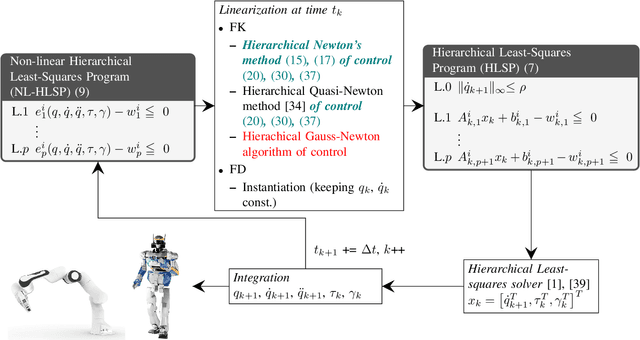
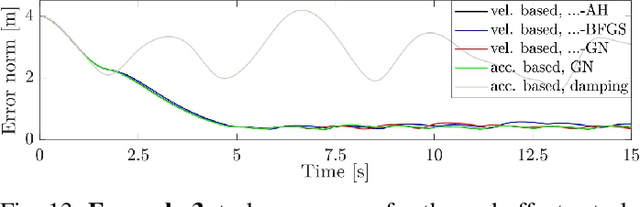
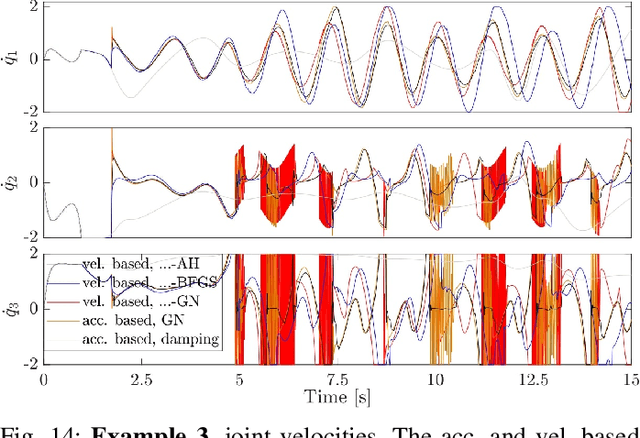
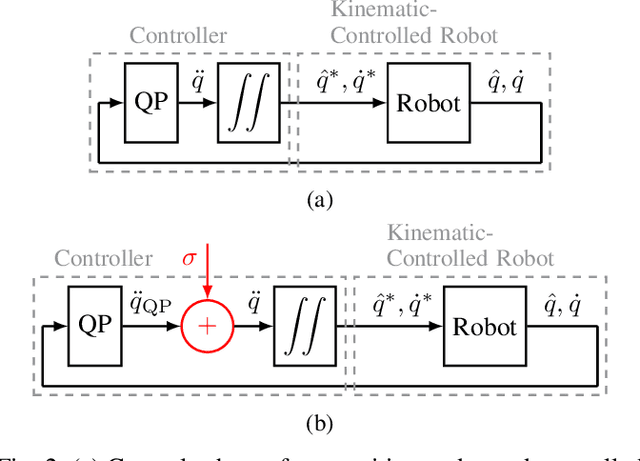
This work links optimization approaches from hierarchical least-squares programming to instantaneous prioritized whole-body robot control. Concretely, we formulate the hierarchical Newton's method which solves prioritized non-linear least-squares problems in a numerically stable fashion even in the presence of kinematic and algorithmic singularities of the approximated kinematic constraints. These results are then transferred to control problems which exhibit the additional variability of time. This is necessary in order to formulate acceleration based controllers and to incorporate the second order dynamics. However, we show that the Newton's method without complicated adaptations is not appropriate in the acceleration domain. We therefore formulate a velocity based controller which exhibits second order proportional derivative convergence characteristics. Our developments are verified in toy robot control scenarios as well as in complex robot experiments which stress the importance of prioritized control and its singularity resolution.

Optimization-Based Control for Dynamic Legged Robots

In a world designed for legs, quadrupeds, bipeds, and humanoids have the opportunity to impact emerging robotics applications from logistics, to agriculture, to home assistance. The goal of this survey is to cover the recent progress toward these applications that has been driven by model-based optimization for the real-time generation and control of movement. The majority of the research community has converged on the idea of generating locomotion control laws by solving an optimal control problem (OCP) in either a model-based or data-driven manner. However, solving the most general of these problems online remains intractable due to complexities from intermittent unidirectional contacts with the environment, and from the many degrees of freedom of legged robots. This survey covers methods that have been pursued to make these OCPs computationally tractable, with specific focus on how environmental contacts are treated, how the model can be simplified, and how these choices affect the numerical solution methods employed. The survey focuses on model-based optimization, covering its recent use in a stand alone fashion, and suggesting avenues for combination with learning-based formulations to further accelerate progress in this growing field.

$\mathcal{N}$IPM-HLSP: An Efficient Interior-Point Method for Hierarchical Least-Squares Programs

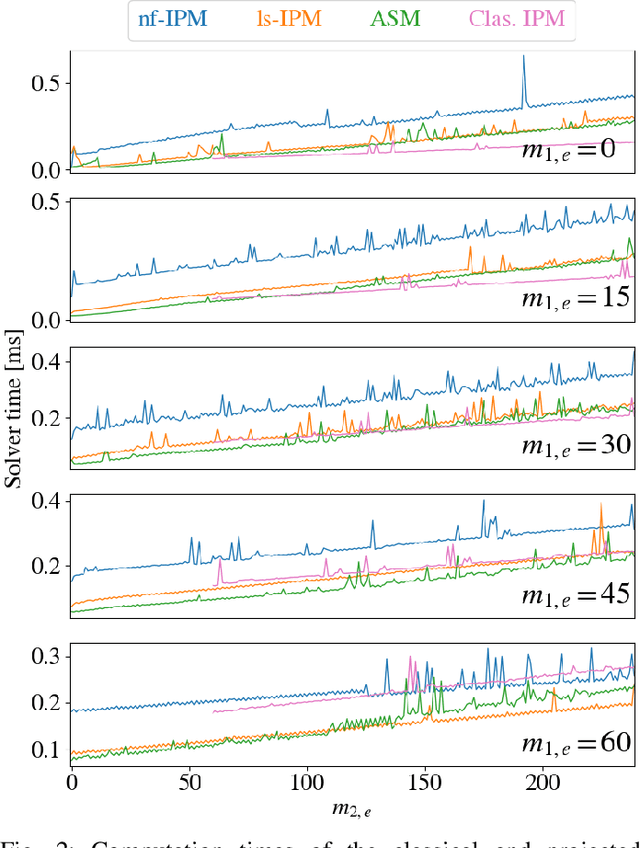
Hierarchical least-squares programs with linear constraints (HLSP) are a type of optimization problem very common in robotics. Each priority level contains an objective in least-squares form which is subject to the linear constraints of the higher priority hierarchy levels. Active-set methods (ASM) are a popular choice for solving them. However, they can perform poorly in terms of computational time if there are large changes of the active set. We therefore propose a computationally efficient primal-dual interior-point method (IPM) for HLSP's which is able to maintain constant numbers of solver iterations in these situations. We base our IPM on the null-space method which requires only a single decomposition per Newton iteration instead of two as it is the case for other IPM solvers. After a priority level has converged we compose a set of active constraints judging upon the dual and project lower priority levels into their null-space. We show that the IPM-HLSP can be expressed in least-squares form which avoids the formation of the quadratic Karush-Kuhn-Tucker (KKT) Hessian. Due to our choice of the null-space basis the IPM-HLSP is as fast as the state-of-the-art ASM-HLSP solver for equality only problems.

Capturability-based Pattern Generation for Walking with Variable Height

Capturability analysis of the linear inverted pendulum (LIP) model enabled walking with constrained height based on the capture point. We generalize this analysis to the variable-height inverted pendulum (VHIP) and show how it enables 3D walking over uneven terrains based on capture inputs. Thanks to a tailored optimization scheme, we can compute these inputs fast enough for real-time model predictive control. We implement this approach as open-source software and demonstrate it in dynamic simulations.

Quotient-Space Motion Planning

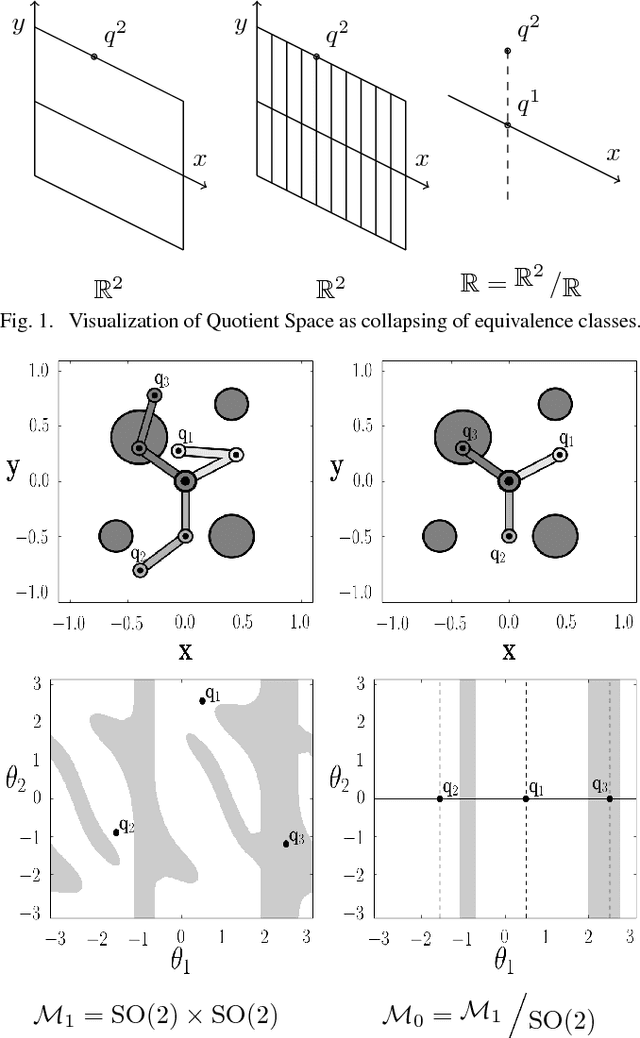
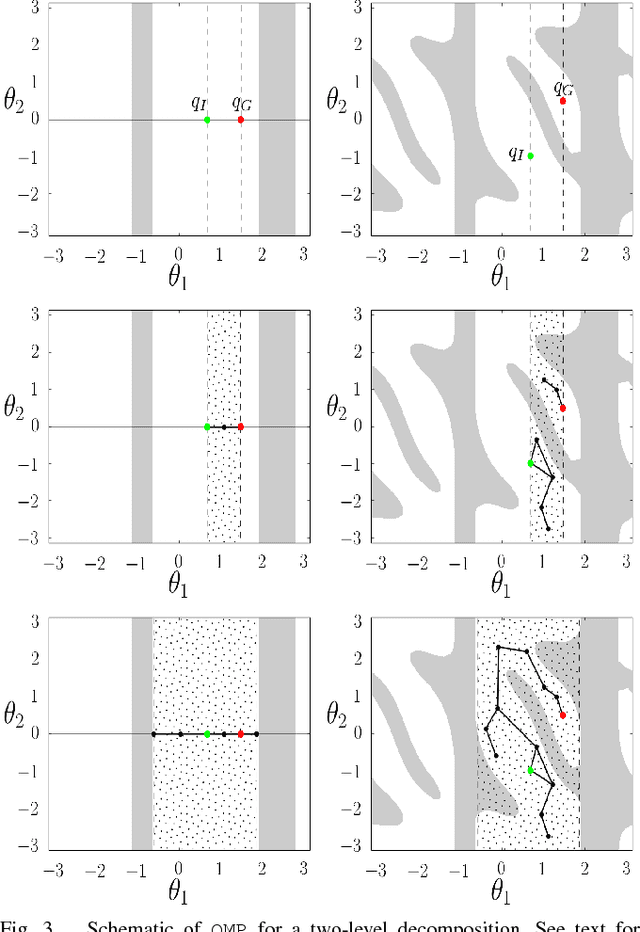
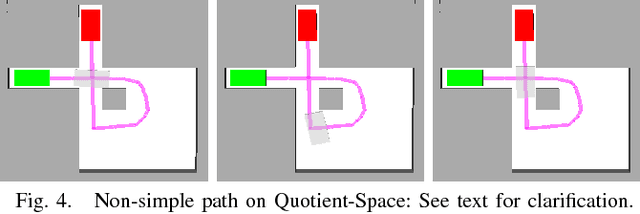
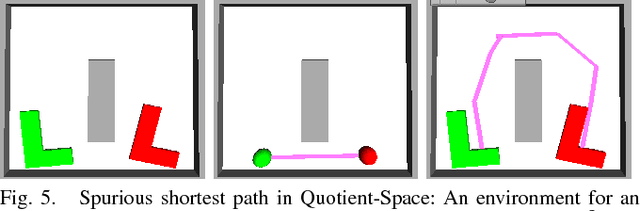
A motion planning algorithm computes the motion of a robot by computing a path through its configuration space. To improve the runtime of motion planning algorithms, we propose to nest robots in each other, creating a nested quotient-space decomposition of the configuration space. Based on this decomposition we define a new roadmap-based motion planning algorithm called the Quotient-space roadMap Planner (QMP). The algorithm starts growing a graph on the lowest dimensional quotient space, switches to the next quotient space once a valid path has been found, and keeps updating the graphs on each quotient space simultaneously until a valid path in the configuration space has been found. We show that this algorithm is probabilistically complete and outperforms a set of state-of-the-art algorithms implemented in the open motion planning library (OMPL).

Identification of Fully Physical Consistent Inertial Parameters using Optimization on Manifolds

This paper presents a new condition, the fully physical consistency for a set of inertial parameters to determine if they can be generated by a physical rigid body. The proposed condition ensure both the positive definiteness and the triangular inequality of 3D inertia matrices as opposed to existing techniques in which the triangular inequality constraint is ignored. This paper presents also a new parametrization that naturally ensures that the inertial parameters are fully physical consistency. The proposed parametrization is exploited to reformulate the inertial identification problem as a manifold optimization problem, that ensures that the identified parameters can always be generated by a physical body. The proposed optimization problem has been validated with a set of experiments on the iCub humanoid robot.