Kai Pfeiffer
NYU Tandon School of Engineering
Sparse Hierarchical Non-Linear Programming for Sparse Inverse Kinematic Planning and Control with Autonomous Goal Selection
Dec 02, 2024


Abstract:Sparse programming is an important tool in robotics, for example in real-time sparse inverse kinematic control with a minimum number of active joints, or autonomous goal selection. However, current approaches are limited to real-time control without consideration of the underlying non-linear problem. This prevents the application to non-linear problems like inverse kinematic planning while the robot autonomously chooses from a set of potential goal positions. Instead, kinematic reachability approximations are used while the robot's whole body motion is considered separately. Furthermore, the sparse constraints are not prioritized for intuitive problem formulation. Lastly, the computational effort of the used standard solvers is cubically dependent on the number of constraints which is problematic in the presence of a large number of possible goals. In this work, we address sparse hierarchical non-linear programs with tools from hierarchical non-linear programming to gain a holistic understanding of the problem at hand. The resulting sequential sparse hierarchical quadratic programming solver scales linearly in the number of constraints and enables the formulation of sparse non-linear equality and inequality constraints on any priority level without feasibility requirements. This enables efficient robot sparse hierarchical inverse kinematic planning and control with autonomous goal selection from a high number of possible goal positions without any reachability approximations.
Efficient Lexicographic Optimization for Prioritized Robot Control and Planning
Mar 14, 2024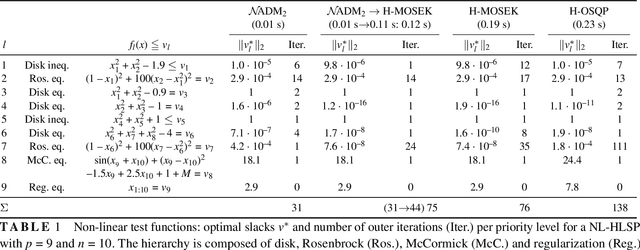
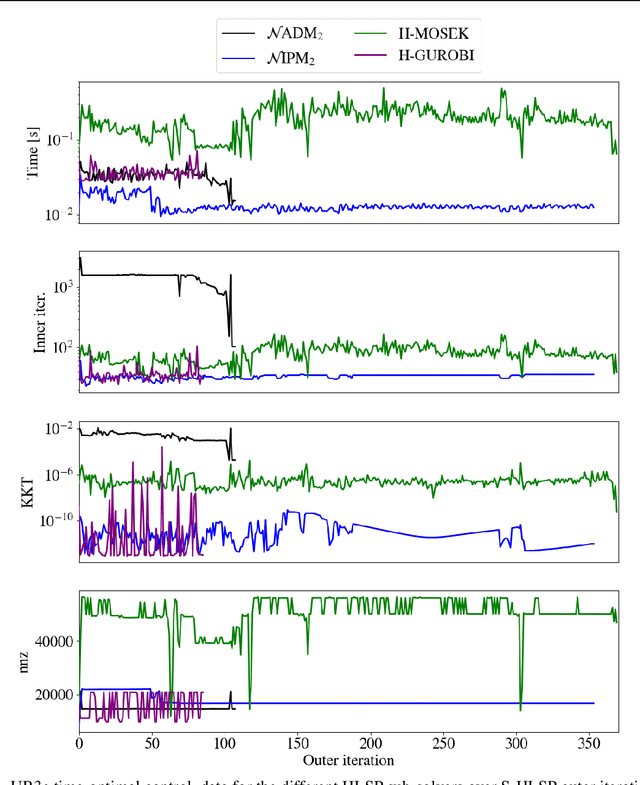
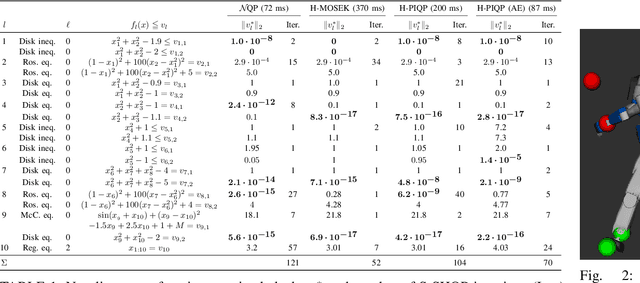
Abstract:In this work, we present several tools for efficient sequential hierarchical least-squares programming (S-HLSP) for lexicographical optimization tailored to robot control and planning. As its main step, S-HLSP relies on approximations of the original non-linear hierarchical least-squares programming (NL-HLSP) to a hierarchical least-squares programming (HLSP) by the hierarchical Newton's method or the hierarchical Gauss-Newton algorithm. We present a threshold adaptation strategy for appropriate switches between the two. This ensures optimality of infeasible constraints, promotes numerical stability when solving the HLSP's and enhances optimality of lower priority levels by avoiding regularized local minima. We introduce the solver $\mathcal{N}$ADM$_2$, an alternating direction method of multipliers for HLSP based on nullspace projections of active constraints. The required basis of nullspace of the active constraints is provided by a computationally efficient turnback algorithm for system dynamics discretized by the Euler method. It is based on an upper bound on the bandwidth of linearly independent column subsets within the linearized constraint matrices. Importantly, an expensive initial rank-revealing matrix factorization is unnecessary. We show how the high sparsity of the basis in the fully-actuated case can be preserved in the under-actuated case. $\mathcal{N}$ADM$_2$ consistently shows faster computations times than competing off-the-shelf solvers on NL-HLSP composed of test-functions and whole-body trajectory optimization for fully-actuated and under-actuated robotic systems. We demonstrate how the inherently lower accuracy solutions of the alternating direction method of multipliers can be used to warm-start the non-linear solver for efficient computation of high accuracy solutions to non-linear hierarchical least-squares programs.
The hierarchical Newton's method for numerically stable prioritized dynamic control
Mar 08, 2023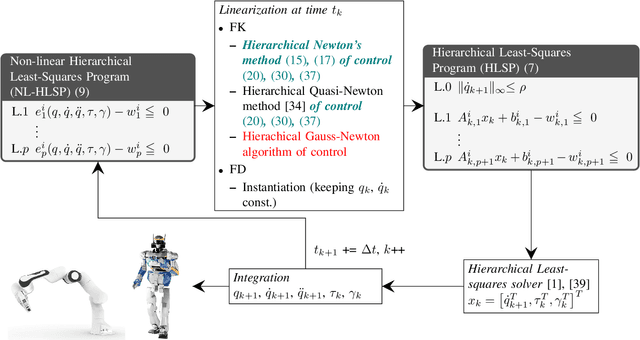
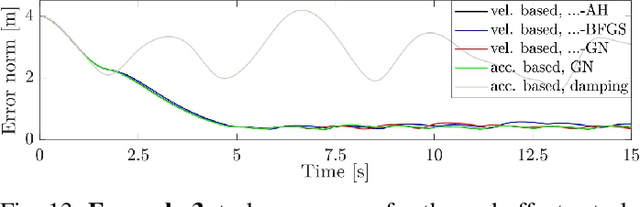
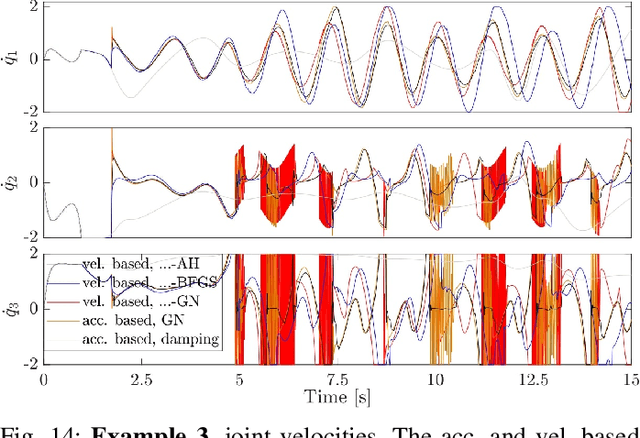
Abstract:This work links optimization approaches from hierarchical least-squares programming to instantaneous prioritized whole-body robot control. Concretely, we formulate the hierarchical Newton's method which solves prioritized non-linear least-squares problems in a numerically stable fashion even in the presence of kinematic and algorithmic singularities of the approximated kinematic constraints. These results are then transferred to control problems which exhibit the additional variability of time. This is necessary in order to formulate acceleration based controllers and to incorporate the second order dynamics. However, we show that the Newton's method without complicated adaptations is not appropriate in the acceleration domain. We therefore formulate a velocity based controller which exhibits second order proportional derivative convergence characteristics. Our developments are verified in toy robot control scenarios as well as in complex robot experiments which stress the importance of prioritized control and its singularity resolution.
Time-Optimal Control via Heaviside Step-Function Approximation
Mar 08, 2023Abstract:Least-squares programming is a popular tool in robotics due to its simplicity and availability of open-source solvers. However, certain problems like sparse programming in the 0- or 1-norm for time-optimal control are not equivalently solvable. In this work we propose a non-linear hierarchical least-squares programming (NL-HLSP) for time-optimal control of non-linear discrete dynamic systems. We use a continuous approximation of the heaviside step function with an additional term that avoids vanishing gradients. We use a simple discretization method by keeping states and controls piece-wise constant between discretization steps. This way we obtain a comparatively easily implementable NL-HLSP in contrast to direct transcription approaches of optimal control. We show that the NL-HLSP indeed recovers the discrete time-optimal control in the limit for resting goal points. We confirm the results in simulation for linear and non-linear control scenarios.
Monte-Carlo Tree Search with Prioritized Node Expansion for Multi-Goal Task Planning
Mar 08, 2023
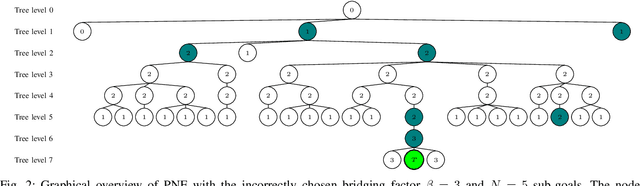
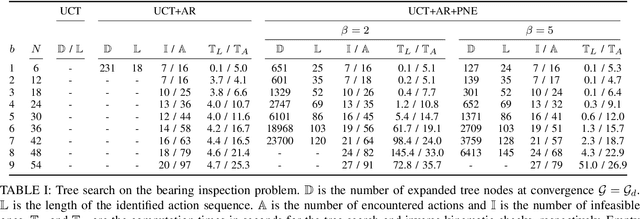
Abstract:Task planning for robots is computationally challenging due to the combinatorial complexity of the possible action space. This fact is amplified if there are several sub-goals to be achieved due to the increased length of the action sequences. In this work, we propose a multi-goal task planning algorithm for deterministic decision processes based on Monte Carlo Tree Search. We augment the algorithm by prioritized node expansion which prioritizes nodes that already have fulfilled some sub-goals. Due to its linear complexity in the number of sub-goals our algorithm is able to identify action sequences of 145 elements to reach the desired goal state with up to 48 sub-goals while the search tree is limited to under 6500 nodes. We use action reduction based on a kinematic reachability criterion to further ease computational complexity. We combine our algorithm with object localization and motion planning and apply it to a real-robot demonstration with two manipulators in an industrial bearing inspection setting.
Path Planning Under Uncertainty to Localize mmWave Sources
Mar 08, 2023
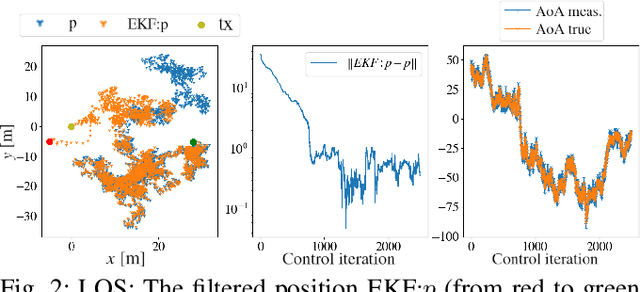

Abstract:In this paper, we study a navigation problem where a mobile robot needs to locate a mmWave wireless signal. Using the directionality properties of the signal, we propose an estimation and path planning algorithm that can efficiently navigate in cluttered indoor environments. We formulate Extended Kalman filters for emitter location estimation in cases where the signal is received in line-of-sight or after reflections. We then propose to plan motion trajectories based on belief-space dynamics in order to minimize the uncertainty of the position estimates. The associated non-linear optimization problem is solved by a state-of-the-art constrained iLQR solver. In particular, we propose a method that can handle a large number of obstacles (~300) with reasonable computation times. We validate the approach in an extensive set of simulations. We show that our estimators can help increase navigation success rate and that planning to reduce estimation uncertainty can improve the overall task completion speed.
Sequential Hierarchical Least-Squares Programming for Prioritized Non-Linear Optimal Control
Feb 23, 2023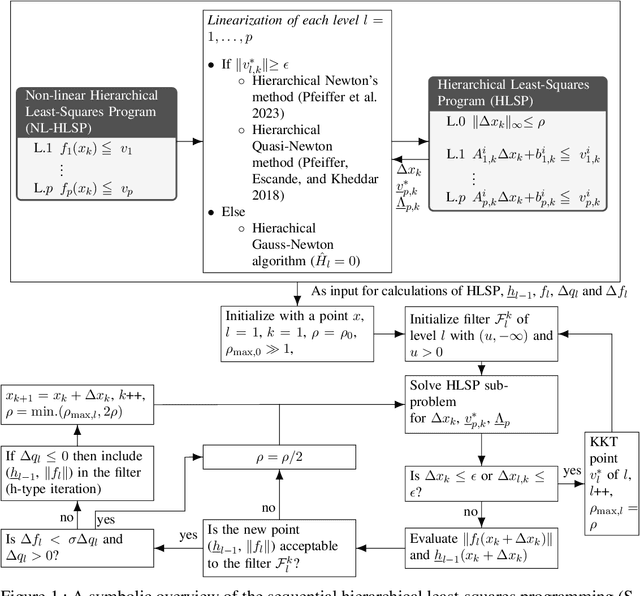
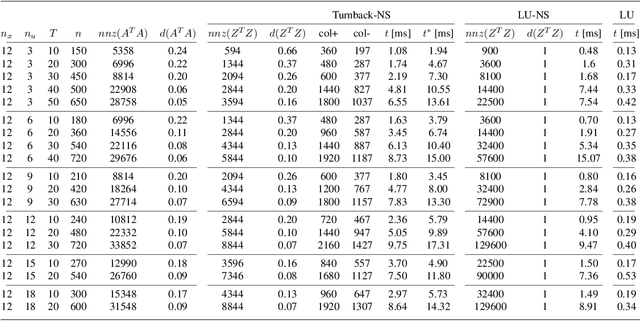

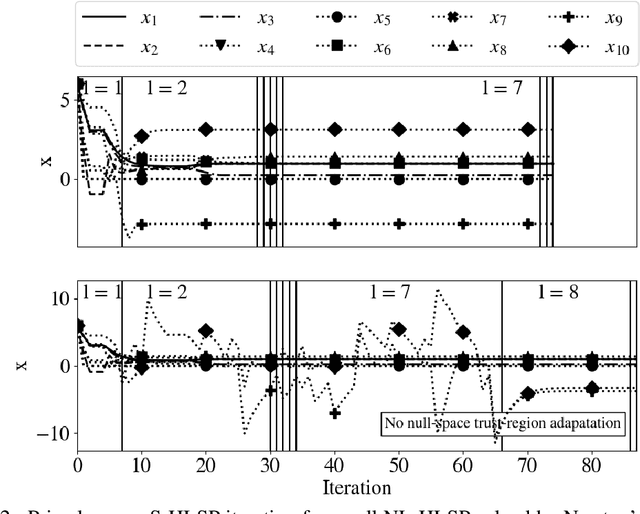
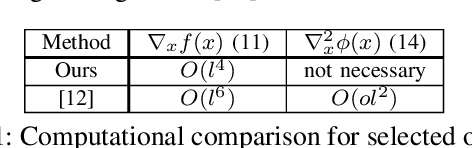
Abstract:We present a sequential hierarchical least-squares programming solver with trust-region and hierarchical step-filter tailored to prioritized non-linear optimal control. It is based on a hierarchical step-filter which resolves each priority level of a non-linear hierarchical least-squares programming via a globally convergent sequential quadratic programming step-filter. Leveraging a condition on the trust-region or the filter initialization, our hierarchical step-filter maintains this global convergence property. The hierarchical least-squares programming sub-problems are solved via a sparse nullspace method based interior point method. It is based on an efficient implementation of the turnback algorithm for the computation of nullspace bases for banded matrices. It is also here that we propose a nullspace trust region adaptation method towards a comprehensive hierarchical step-filter. We demonstrate the computational efficiency of the hierarchical solver on typical test functions like the Rosenbrock and Himmelblau's functions, inverse kinematics problems and optimal control.
Millimeter Wave Wireless Assisted Robot Navigation with Link State Classification
Nov 05, 2021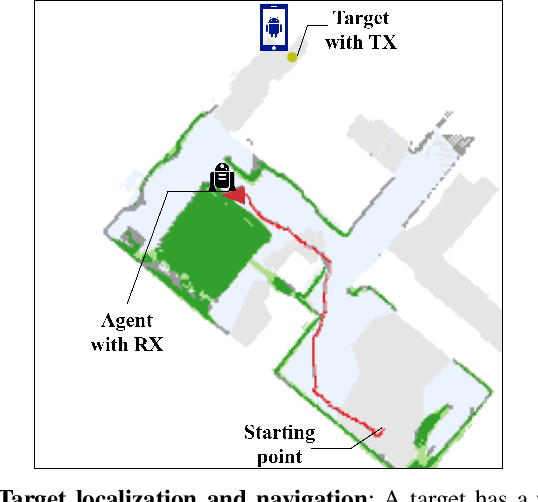
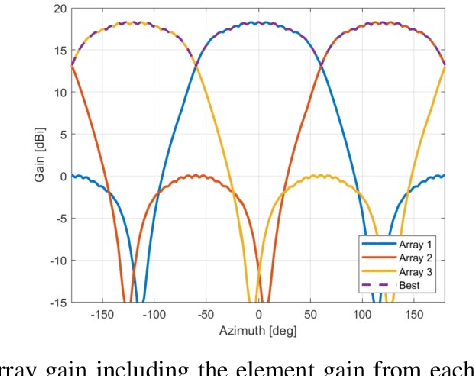
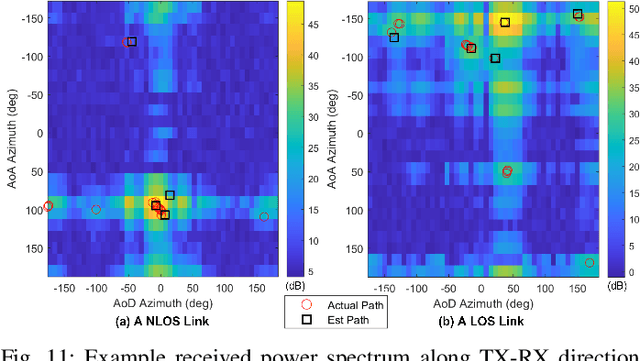
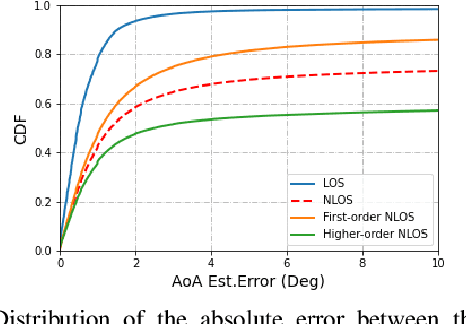
Abstract:The millimeter wave (mmWave) bands have attracted considerable attention for high precision localization applications due to the ability to capture high angular and temporal resolution measurements. This paper explores mmWave-based positioning for a target localization problem where a fixed target broadcasts mmWave signals and a mobile robotic agent attempts to listen to the signals to locate and navigate to the target. A three strage procedure is proposed: First, the mobile agent uses tensor decomposition methods to detect the wireless paths and their angles. Second, a machine-learning trained classifier is then used to predict the link state, meaning if the strongest path is line-of-sight (LOS) or non-LOS (NLOS). For the NLOS case, the link state predictor also determines if the strongest path arrived via one or more reflections. Third, based on the link state, the agent either follows the estimated angles or explores the environment. The method is demonstrated on a large dataset of indoor environments supplemented with ray tracing to simulate the wireless propagation. The path estimation and link state classification are also integrated into a state-ofthe-art neural simultaneous localization and mapping (SLAM) module to augment camera and LIDAR-based navigation. It is shown that the link state classifier can successfully generalize to completely new environments outside the training set. In addition, the neural-SLAM module with the wireless path estimation and link state classifier provides rapid navigation to the target, close to a baseline that knows the target location.
$\mathcal{N}$IPM-HLSP: An Efficient Interior-Point Method for Hierarchical Least-Squares Programs
Jun 25, 2021
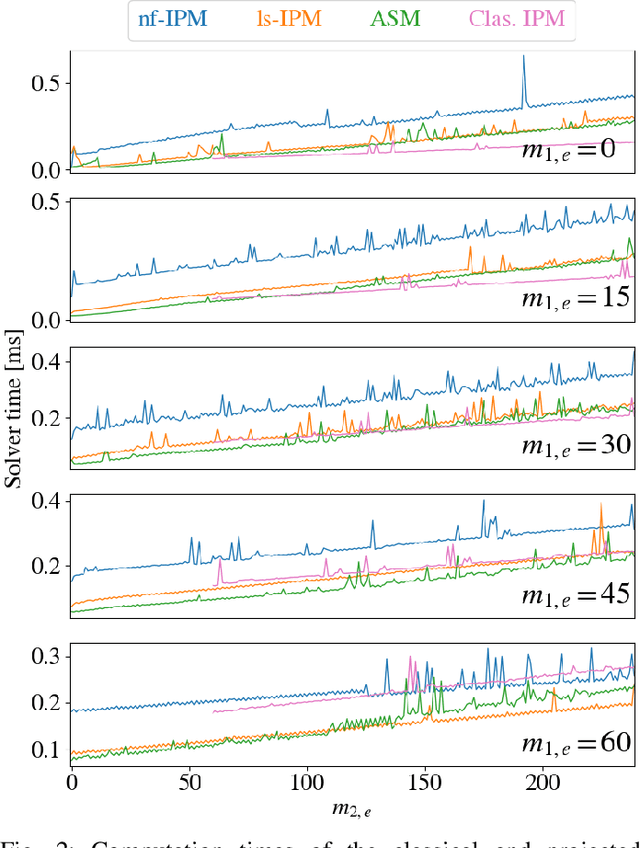


Abstract:Hierarchical least-squares programs with linear constraints (HLSP) are a type of optimization problem very common in robotics. Each priority level contains an objective in least-squares form which is subject to the linear constraints of the higher priority hierarchy levels. Active-set methods (ASM) are a popular choice for solving them. However, they can perform poorly in terms of computational time if there are large changes of the active set. We therefore propose a computationally efficient primal-dual interior-point method (IPM) for HLSP's which is able to maintain constant numbers of solver iterations in these situations. We base our IPM on the null-space method which requires only a single decomposition per Newton iteration instead of two as it is the case for other IPM solvers. After a priority level has converged we compose a set of active constraints judging upon the dual and project lower priority levels into their null-space. We show that the IPM-HLSP can be expressed in least-squares form which avoids the formation of the quadratic Karush-Kuhn-Tucker (KKT) Hessian. Due to our choice of the null-space basis the IPM-HLSP is as fast as the state-of-the-art ASM-HLSP solver for equality only problems.
Enabling Remote Whole-Body Control with 5G Edge Computing
Aug 19, 2020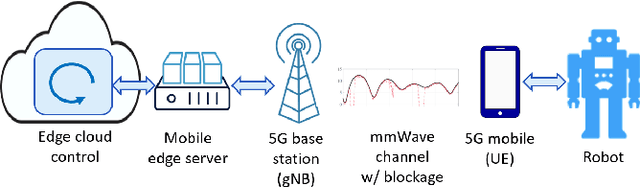
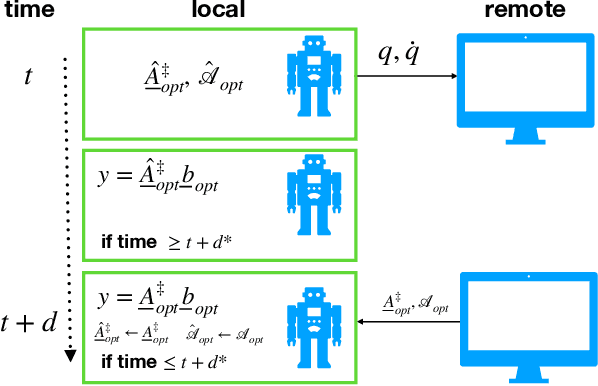
Abstract:Real-world applications require light-weight, energy-efficient, fully autonomous robots. Yet, increasing autonomy is oftentimes synonymous with escalating computational requirements. It might thus be desirable to offload intensive computation--not only sensing and planning, but also low-level whole-body control--to remote servers in order to reduce on-board computational needs. Fifth Generation (5G) wireless cellular technology, with its low latency and high bandwidth capabilities, has the potential to unlock cloud-based high performance control of complex robots. However, state-of-the-art control algorithms for legged robots can only tolerate very low control delays, which even ultra-low latency 5G edge computing can sometimes fail to achieve. In this work, we investigate the problem of cloud-based whole-body control of legged robots over a 5G link. We propose a novel approach that consists of a standard optimization-based controller on the network edge and a local linear, approximately optimal controller that significantly reduces on-board computational needs while increasing robustness to delay and possible loss of communication. Simulation experiments on humanoid balancing and walking tasks that includes a realistic 5G communication model demonstrate significant improvement of the reliability of robot locomotion under jitter and delays likely to experienced in 5G wireless links.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge