Sequential Hierarchical Least-Squares Programming for Prioritized Non-Linear Optimal Control

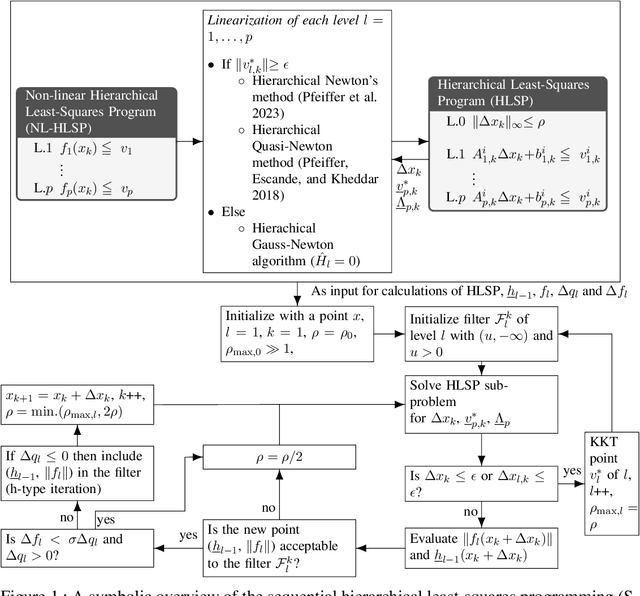
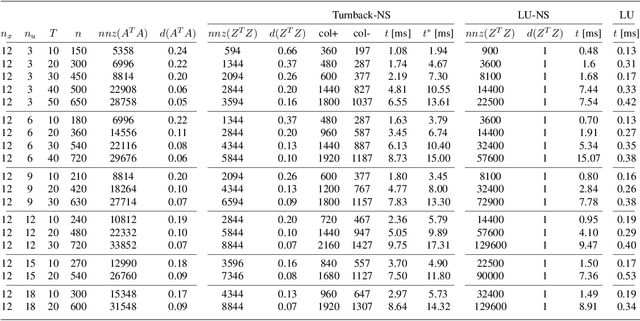
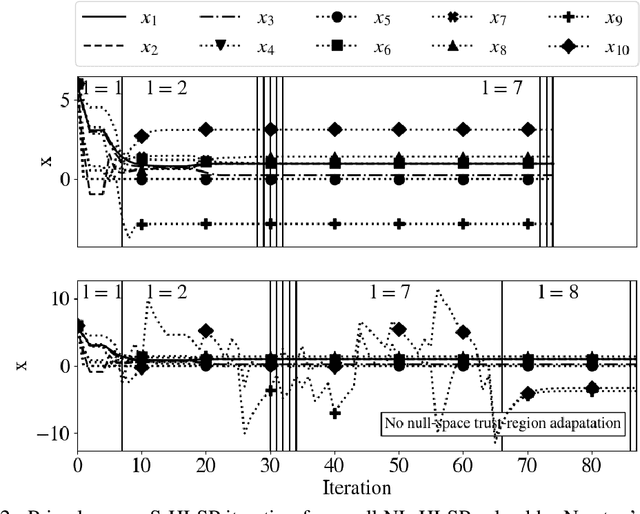
We present a sequential hierarchical least-squares programming solver with trust-region and hierarchical step-filter tailored to prioritized non-linear optimal control. It is based on a hierarchical step-filter which resolves each priority level of a non-linear hierarchical least-squares programming via a globally convergent sequential quadratic programming step-filter. Leveraging a condition on the trust-region or the filter initialization, our hierarchical step-filter maintains this global convergence property. The hierarchical least-squares programming sub-problems are solved via a sparse nullspace method based interior point method. It is based on an efficient implementation of the turnback algorithm for the computation of nullspace bases for banded matrices. It is also here that we propose a nullspace trust region adaptation method towards a comprehensive hierarchical step-filter. We demonstrate the computational efficiency of the hierarchical solver on typical test functions like the Rosenbrock and Himmelblau's functions, inverse kinematics problems and optimal control.