Inverse-Dynamics MPC via Nullspace Resolution
Paper and Code
Sep 12, 2022

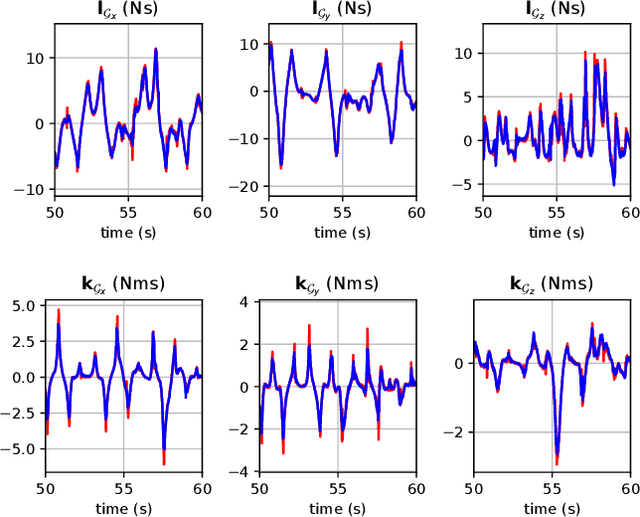
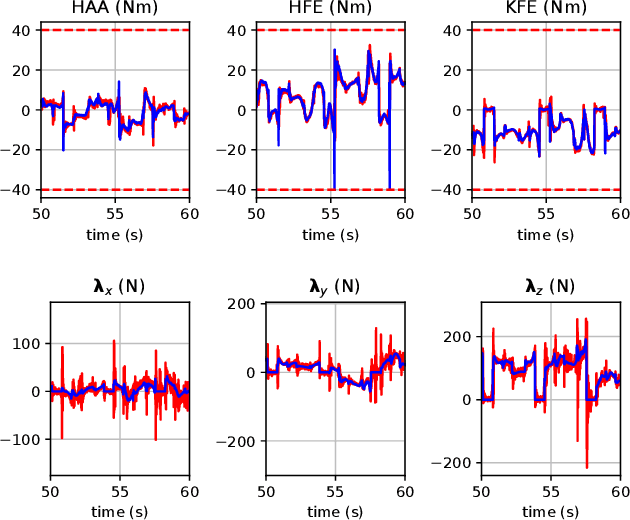
Optimal control (OC) using inverse dynamics provides numerical benefits such as coarse optimization, cheaper computation of derivatives, and a high convergence rate. However, in order to take advantage of these benefits in model predictive control (MPC) for legged robots, it is crucial to handle its large number of equality constraints efficiently. To accomplish this, we first (i) propose a novel approach to handle equality constraints based on nullspace parametrization. Our approach balances optimality, and both dynamics and equality-constraint feasibility appropriately, which increases the basin of attraction to good local minima. To do so, we then (ii) adapt our feasibility-driven search by incorporating a merit function. Furthermore, we introduce (iii) a condensed formulation of the inverse dynamics that considers arbitrary actuator models. We also develop (iv) a novel MPC based on inverse dynamics within a perception locomotion framework. Finally, we present (v) a theoretical comparison of optimal control with the forward and inverse dynamics, and evaluate both numerically. Our approach enables the first application of inverse-dynamics MPC on hardware, resulting in state-of-the-art dynamic climbing on the ANYmal robot. We benchmark it over a wide range of robotics problems and generate agile and complex maneuvers. We show the computational reduction of our nullspace resolution and condensed formulation (up to 47.3%). We provide evidence of the benefits of our approach by solving coarse optimization problems with a high convergence rate (up to 10 Hz of discretization). Our algorithm is publicly available inside CROCODDYL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge