Optimal Control for Articulated Soft Robots

Soft robots can execute tasks with safer interactions. However, control techniques that can effectively exploit the systems' capabilities are still missing. Differential dynamic programming (DDP) has emerged as a promising tool for achieving highly dynamic tasks. But most of the literature deals with applying DDP to articulated soft robots by using numerical differentiation, in addition to using pure feed-forward control to perform explosive tasks. Further, underactuated compliant robots are known to be difficult to control and the use of DDP-based algorithms to control them is not yet addressed. We propose an efficient DDP-based algorithm for trajectory optimization of articulated soft robots that can optimize the state trajectory, input torques, and stiffness profile. We provide an efficient method to compute the forward dynamics and the analytical derivatives of series elastic actuators (SEA)/variable stiffness actuators (VSA) and underactuated compliant robots. We present a state-feedback controller that uses locally optimal feedback policies obtained from DDP. We show through simulations and experiments that the use of feedback is crucial in improving the performance and stabilization properties of various tasks. We also show that the proposed method can be used to plan and control underactuated compliant robots, with varying degrees of underactuation effectively.

Inverse-Dynamics MPC via Nullspace Resolution

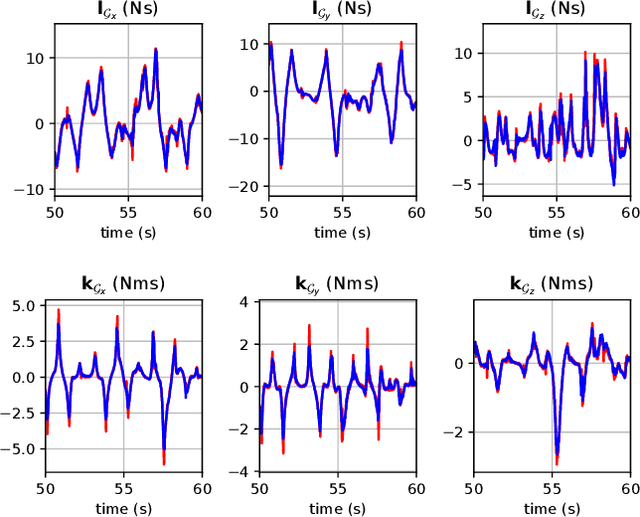
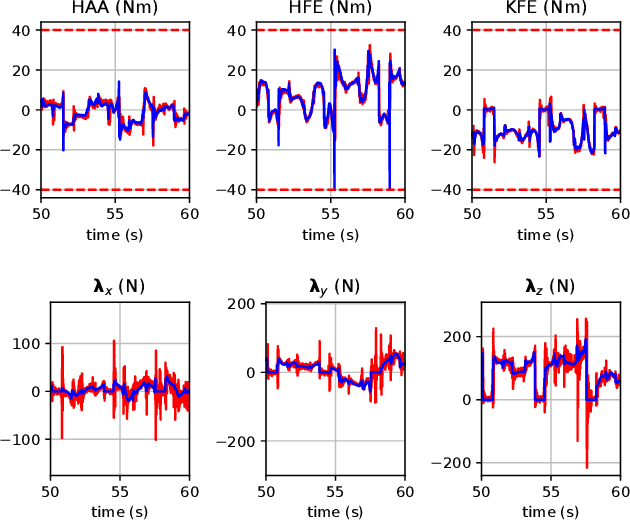
Optimal control (OC) using inverse dynamics provides numerical benefits such as coarse optimization, cheaper computation of derivatives, and a high convergence rate. However, in order to take advantage of these benefits in model predictive control (MPC) for legged robots, it is crucial to handle its large number of equality constraints efficiently. To accomplish this, we first (i) propose a novel approach to handle equality constraints based on nullspace parametrization. Our approach balances optimality, and both dynamics and equality-constraint feasibility appropriately, which increases the basin of attraction to good local minima. To do so, we then (ii) adapt our feasibility-driven search by incorporating a merit function. Furthermore, we introduce (iii) a condensed formulation of the inverse dynamics that considers arbitrary actuator models. We also develop (iv) a novel MPC based on inverse dynamics within a perception locomotion framework. Finally, we present (v) a theoretical comparison of optimal control with the forward and inverse dynamics, and evaluate both numerically. Our approach enables the first application of inverse-dynamics MPC on hardware, resulting in state-of-the-art dynamic climbing on the ANYmal robot. We benchmark it over a wide range of robotics problems and generate agile and complex maneuvers. We show the computational reduction of our nullspace resolution and condensed formulation (up to 47.3%). We provide evidence of the benefits of our approach by solving coarse optimization problems with a high convergence rate (up to 10 Hz of discretization). Our algorithm is publicly available inside CROCODDYL.