Perceptive Locomotion through Whole-Body MPC and Optimal Region Selection

Real-time synthesis of legged locomotion maneuvers in challenging industrial settings is still an open problem, requiring simultaneous determination of footsteps locations several steps ahead while generating whole-body motions close to the robot's limits. State estimation and perception errors impose the practical constraint of fast re-planning motions in a model predictive control (MPC) framework. We first observe that the computational limitation of perceptive locomotion pipelines lies in the combinatorics of contact surface selection. Re-planning contact locations on selected surfaces can be accomplished at MPC frequencies (50-100 Hz). Then, whole-body motion generation typically follows a reference trajectory for the robot base to facilitate convergence. We propose removing this constraint to robustly address unforeseen events such as contact slipping, by leveraging a state-of-the-art whole-body MPC (Croccodyl). Our contributions are integrated into a complete framework for perceptive locomotion, validated under diverse terrain conditions, and demonstrated in challenging trials that push the robot's actuation limits, as well as in the ICRA 2023 quadruped challenge simulation.

Topology-Based MPC for Automatic Footstep Placement and Contact Surface Selection

State-of-the-art approaches to footstep planning assume reduced-order dynamics when solving the combinatorial problem of selecting contact surfaces in real time. However, in exchange for computational efficiency, these approaches ignore joint torque limits and limb dynamics. In this work, we address these limitations by presenting a topology-based approach that enables~\gls{mpc} to simultaneously plan full-body motions, torque commands, footstep placements, and contact surfaces in real time. To determine if a robot's foot is inside a contact surface, we borrow the winding number concept from topology. We then use this winding number and potential field to create a contact-surface penalty function. By using this penalty function,~\gls{mpc} can select a contact surface from all candidate surfaces in the vicinity and determine footstep placements within it. We demonstrate the benefits of our approach by showing the impact of considering full-body dynamics, which includes joint torque limits and limb dynamics, on the selection of footstep placements and contact surfaces. Furthermore, we validate the feasibility of deploying our topology-based approach in an~\gls{mpc} scheme and explore its potential capabilities through a series of experimental and simulation trials.

Inverse-Dynamics MPC via Nullspace Resolution

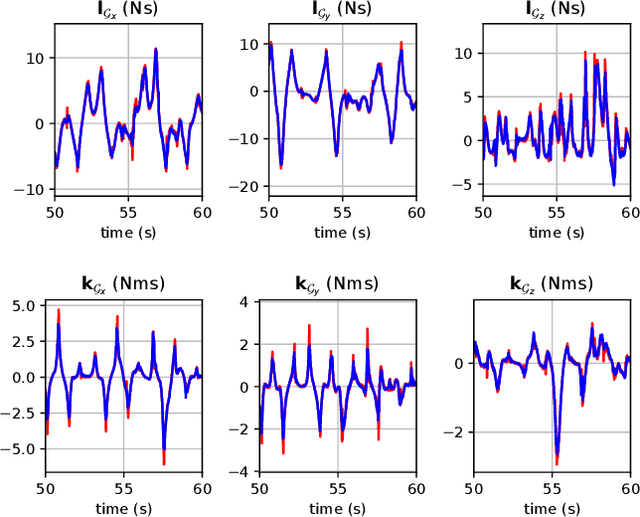
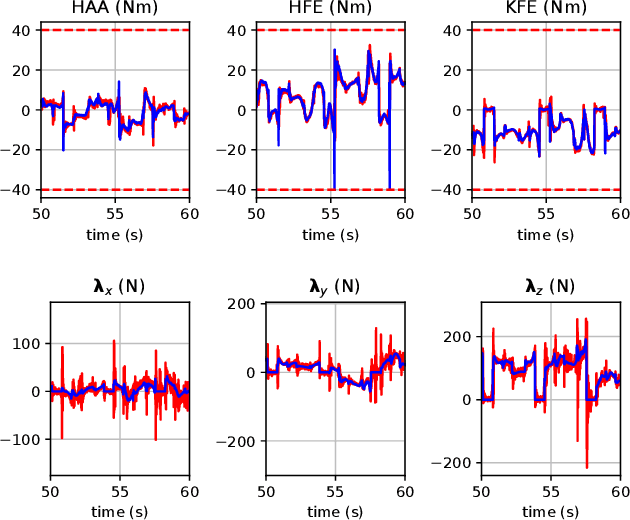
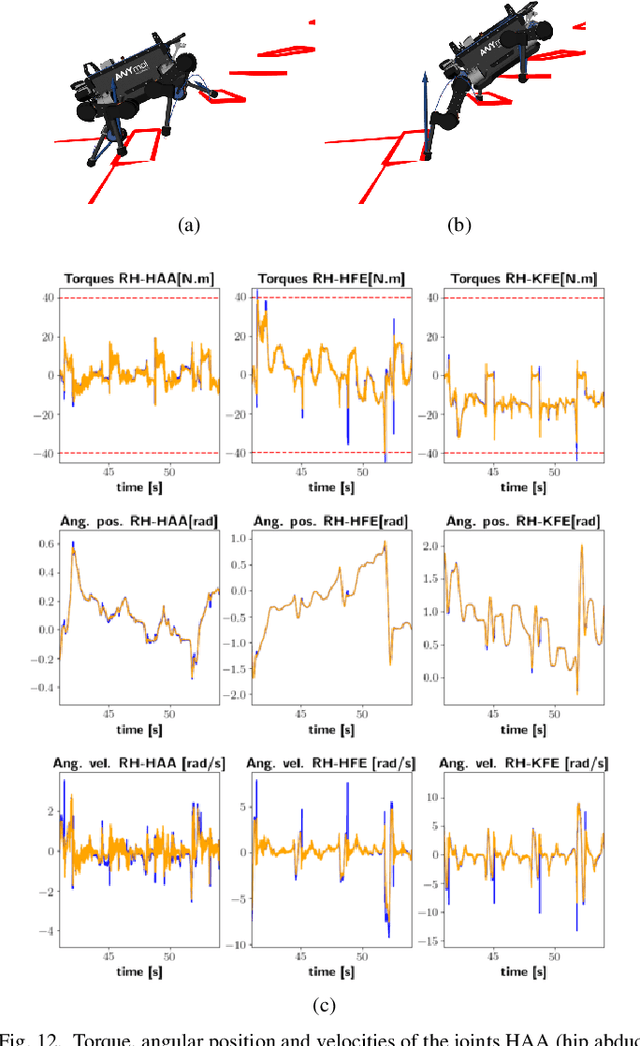
Optimal control (OC) using inverse dynamics provides numerical benefits such as coarse optimization, cheaper computation of derivatives, and a high convergence rate. However, in order to take advantage of these benefits in model predictive control (MPC) for legged robots, it is crucial to handle its large number of equality constraints efficiently. To accomplish this, we first (i) propose a novel approach to handle equality constraints based on nullspace parametrization. Our approach balances optimality, and both dynamics and equality-constraint feasibility appropriately, which increases the basin of attraction to good local minima. To do so, we then (ii) adapt our feasibility-driven search by incorporating a merit function. Furthermore, we introduce (iii) a condensed formulation of the inverse dynamics that considers arbitrary actuator models. We also develop (iv) a novel MPC based on inverse dynamics within a perception locomotion framework. Finally, we present (v) a theoretical comparison of optimal control with the forward and inverse dynamics, and evaluate both numerically. Our approach enables the first application of inverse-dynamics MPC on hardware, resulting in state-of-the-art dynamic climbing on the ANYmal robot. We benchmark it over a wide range of robotics problems and generate agile and complex maneuvers. We show the computational reduction of our nullspace resolution and condensed formulation (up to 47.3%). We provide evidence of the benefits of our approach by solving coarse optimization problems with a high convergence rate (up to 10 Hz of discretization). Our algorithm is publicly available inside CROCODDYL.