Convex strategies for trajectory optimisation: application to the Polytope Traversal Problem
Paper and Code
Sep 16, 2021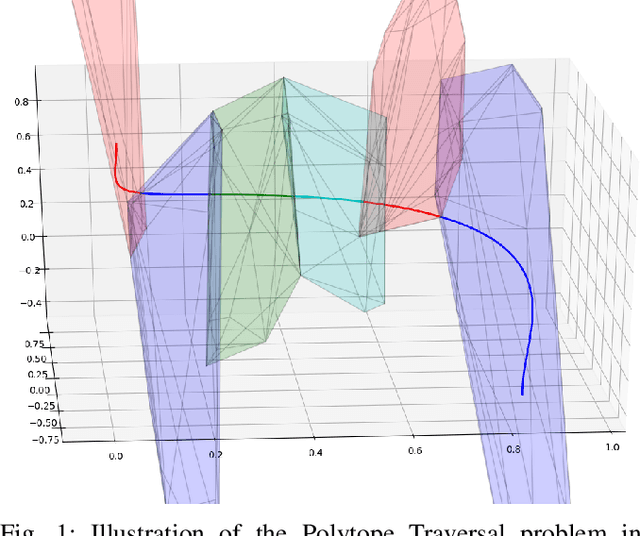
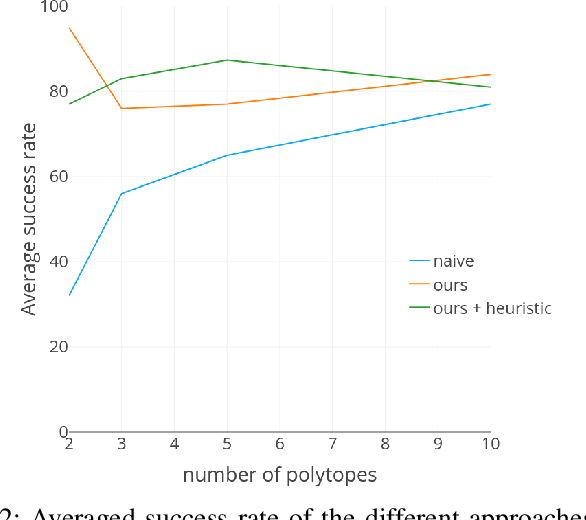
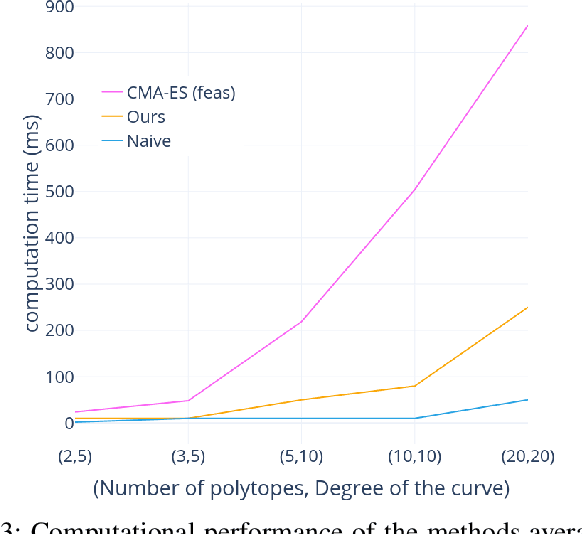
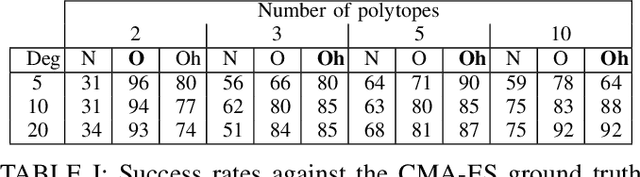
Non-linear Trajectory Optimisation (TO) methods require good initial guesses to converge to a locally optimal solution. A feasible guess can often be obtained by allocating a large amount of time for the trajectory to complete. However for unstable dynamical systems such as humanoid robots, this quasi-static assumption does not always hold. We propose a conservative formulation of the TO problem that simultaneously computes a feasible path and its time allocation. The problem is solved as an efficient convex optimisation problem guaranteed to converge to a locally optimal solution. The interest of the approach is illustrated with the computation of feasible trajectories that traverse sequentially a sequence of polytopes. We demonstrate that on instances of the problem where the quasi static solutions are not admissible, our approach is able to find a feasible solution with a success rate above $80 \%$ in all the scenarios considered, in less than 10ms for problems involving traversing less than 5 polytopes and less than 1s for problems involving 20 polytopes, thus demonstrating its ability to reliably provide initial guesses to advanced non linear solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge