Differentiable Optimal Control via Differential Dynamic Programming

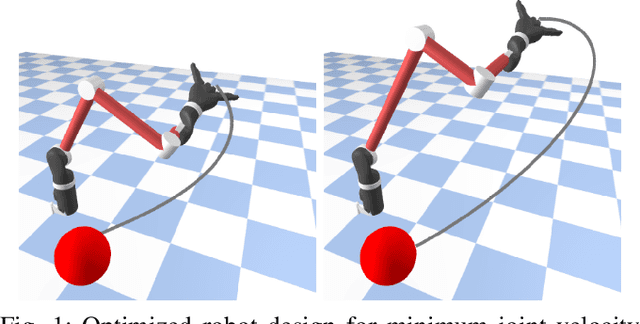
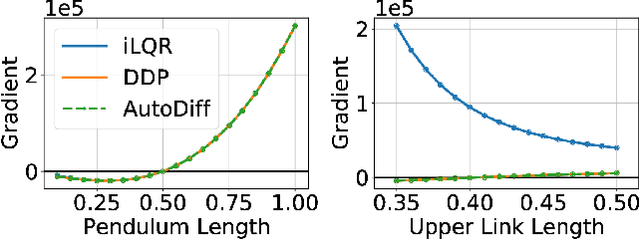
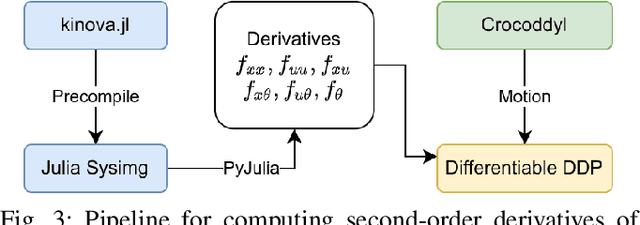
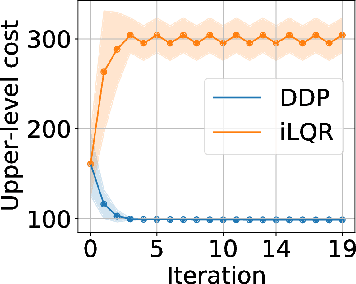
Robot design optimization, imitation learning and system identification share a common problem which requires optimization over robot or task parameters at the same time as optimizing the robot motion. To solve these problems, we can use differentiable optimal control for which the gradients of the robot's motion with respect to the parameters are required. We propose a method to efficiently compute these gradients analytically via the differential dynamic programming (DDP) algorithm using sensitivity analysis (SA). We show that we must include second-order dynamics terms when computing the gradients. However, we do not need to include them when computing the motion. We validate our approach on the pendulum and double pendulum systems. Furthermore, we compare against using the derivatives of the iterative linear quadratic regulator (iLQR), which ignores these second-order terms everywhere, on a co-design task for the Kinova arm, where we optimize the link lengths of the robot for a target reaching task. We show that optimizing using iLQR gradients diverges as ignoring the second-order dynamics affects the computation of the derivatives. Instead, optimizing using DDP gradients converges to the same optimum for a range of initial designs allowing our formulation to scale to complex systems.

Co-Designing Robots by Differentiating Motion Solvers

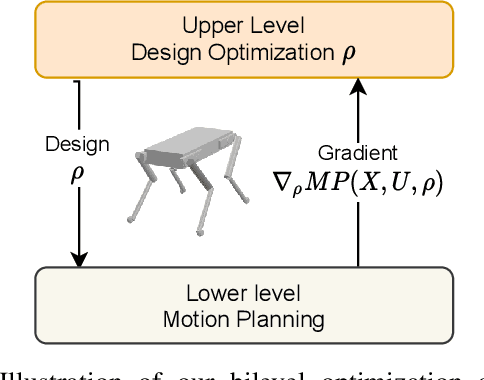
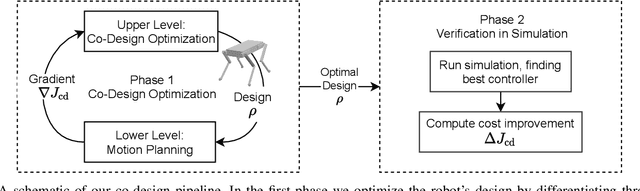
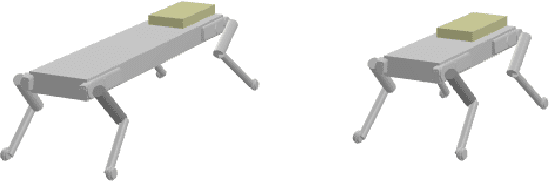
We present a novel algorithm for the computational co-design of legged robots and dynamic maneuvers. Current state-of-the-art approaches are based on random sampling or concurrent optimization. A few recently proposed methods explore the relationship between the gradient of the optimal motion and robot design. Inspired by these approaches, we propose a bilevel optimization approach that exploits the derivatives of the motion planning sub-problem (the inner level) without simplifying assumptions on its structure. Our approach can quickly optimize the robot's morphology while considering its full dynamics, joint limits and physical constraints such as friction cones. It has a faster convergence rate and greater scalability for larger design problems than state-of-the-art approaches based on sampling methods. It also allows us to handle constraints such as the actuation limits, which are important for co-designing dynamic maneuvers. We demonstrate these capabilities by studying jumping and trotting gaits under different design metrics and verify our results in a physics simulator. For these cases, our algorithm converges in less than a third of the number of iterations needed for sampling approaches, and the computation time scales linearly.

Sparsity-Inducing Optimal Control via Differential Dynamic Programming

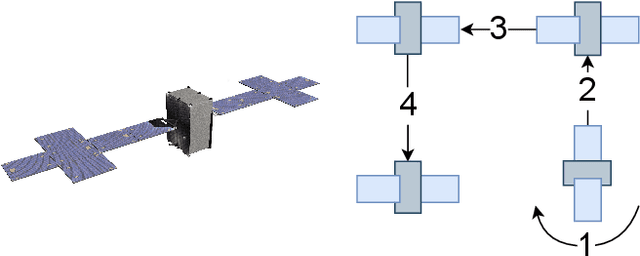
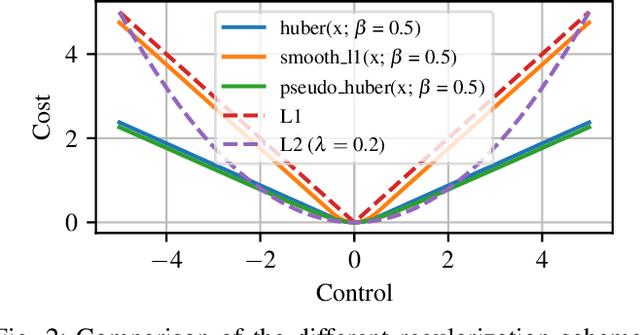
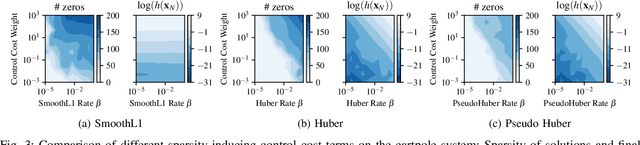
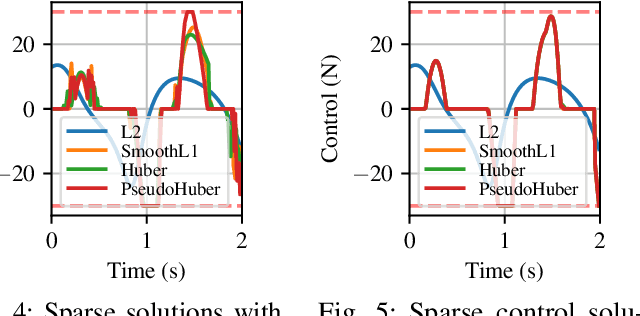
Optimal control is a popular approach to synthesize highly dynamic motion. Commonly, L2 regularization is used on the control inputs in order to minimize energy used and to ensure smoothness of the control inputs. However, for some systems, such as satellites, the control needs to be applied in sparse bursts due to how the propulsion system operates. In this paper, we study approaches to induce sparsity in optimal control solutions---namely via smooth L1 and Huber regularization penalties. We apply these loss terms to state-of-the-art Differential Dynamic Programming (DDP)-based solvers to create a family of sparsity-inducing optimal control methods. We analyze and compare the effect of the different losses on inducing sparsity, their numerical conditioning, their impact on convergence, and discuss hyperparameter settings. We demonstrate our method in simulation and hardware experiments on canonical dynamics systems, control of satellites, and the NASA Valkyrie humanoid robot. We provide an implementation of our method and all examples for reproducibility on GitHub.

Memory Clustering using Persistent Homology for Multimodality- and Discontinuity-Sensitive Learning of Optimal Control Warm-starts

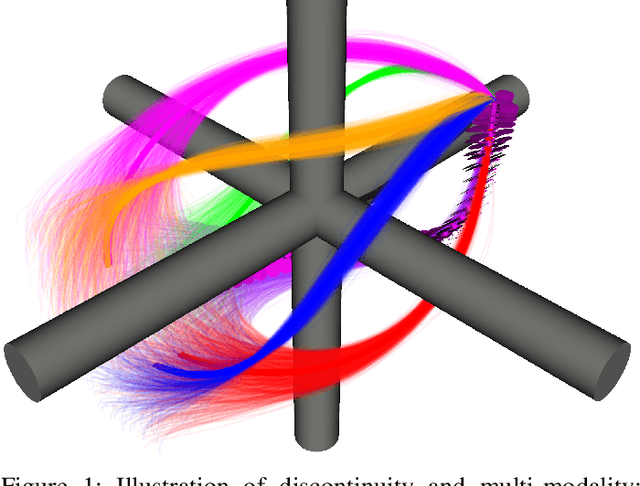
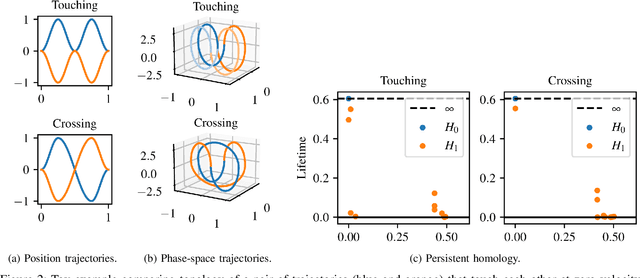
Shooting methods are an efficient approach to solving nonlinear optimal control problems. As they use local optimization, they exhibit favorable convergence when initialized with a good warm-start but may not converge at all if provided with a poor initial guess. Recent work has focused on providing an initial guess from a learned model trained on samples generated during an offline exploration of the problem space. However, in practice the solutions contain discontinuities introduced by system dynamics or the environment. Additionally, in many cases multiple equally suitable, i.e., multi-modal, solutions exist to solve a problem. Classic learning approaches smooth across the boundary of these discontinuities and thus generalize poorly. In this work, we apply tools from algebraic topology to extract information on the underlying structure of the solution space. In particular, we introduce a method based on persistent homology to automatically cluster the dataset of precomputed solutions to obtain different candidate initial guesses. We then train a Mixture-of-Experts within each cluster to predict initial guesses and provide a comparison with modality-agnostic learning. We demonstrate our method on a cart-pole toy problem and a quadrotor avoiding obstacles, and show that clustering samples based on inherent structure improves the warm-start quality.

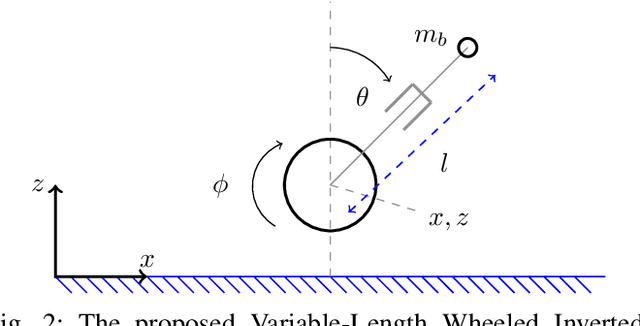
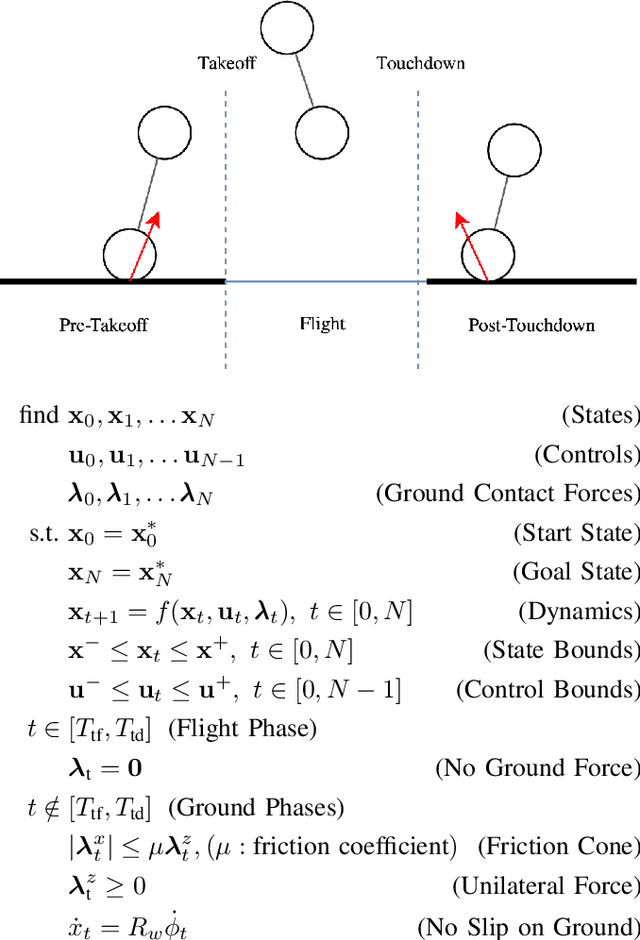
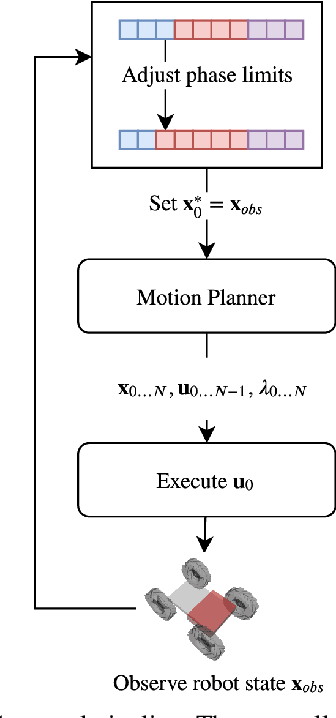
Modeling and Control of a Hybrid Wheeled Jumping Robot

In this paper, we study a wheeled robot with a prismatic extension joint. This allows the robot to build up momentum to perform jumps over obstacles and to swing up to the upright position after the loss of balance. We propose a template model for the class of such two-wheeled jumping robots. This model can be considered as the simplest wheeled-legged system. We provide an analytical derivation of the system dynamics which we use inside a model predictive controller (MPC). We study the behavior of the model and demonstrate highly dynamic motions such as swing-up and jumping. Furthermore, these motions are discovered through optimization from first principles. We evaluate the controller on a variety of tasks and uneven terrains in a simulator.

Dynamic Likelihood-free Inference via Ratio Estimation (DIRE)

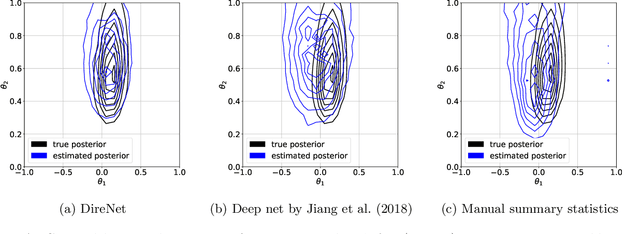
Parametric statistical models that are implicitly defined in terms of a stochastic data generating process are used in a wide range of scientific disciplines because they enable accurate modeling. However, learning the parameters from observed data is generally very difficult because their likelihood function is typically intractable. Likelihood-free Bayesian inference methods have been proposed which include the frameworks of approximate Bayesian computation (ABC), synthetic likelihood, and its recent generalization that performs likelihood-free inference by ratio estimation (LFIRE). A major difficulty in all these methods is choosing summary statistics that reduce the dimensionality of the data to facilitate inference. While several methods for choosing summary statistics have been proposed for ABC, the literature for synthetic likelihood and LFIRE is very thin to date. We here address this gap in the literature, focusing on the important special case of time-series models. We show that convolutional neural networks trained to predict the input parameters from the data provide suitable summary statistics for LFIRE. On a wide range of time-series models, a single neural network architecture produced equally or more accurate posteriors than alternative methods.