Memory Clustering using Persistent Homology for Multimodality- and Discontinuity-Sensitive Learning of Optimal Control Warm-starts

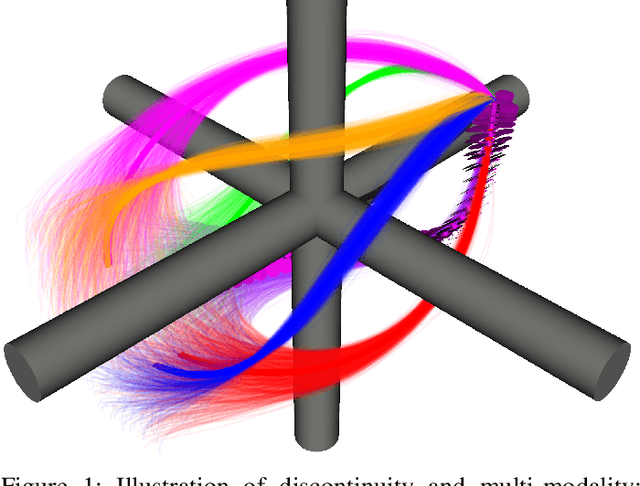
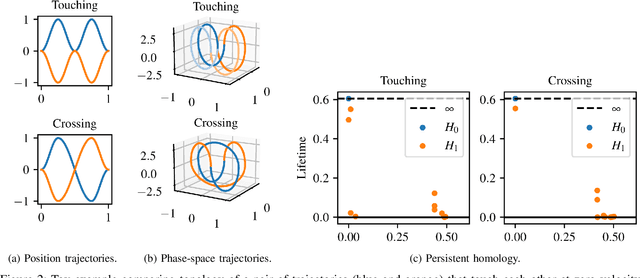
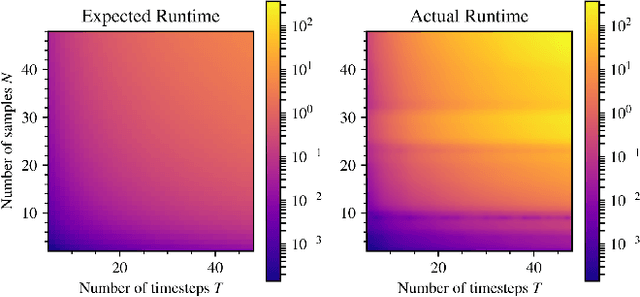
Shooting methods are an efficient approach to solving nonlinear optimal control problems. As they use local optimization, they exhibit favorable convergence when initialized with a good warm-start but may not converge at all if provided with a poor initial guess. Recent work has focused on providing an initial guess from a learned model trained on samples generated during an offline exploration of the problem space. However, in practice the solutions contain discontinuities introduced by system dynamics or the environment. Additionally, in many cases multiple equally suitable, i.e., multi-modal, solutions exist to solve a problem. Classic learning approaches smooth across the boundary of these discontinuities and thus generalize poorly. In this work, we apply tools from algebraic topology to extract information on the underlying structure of the solution space. In particular, we introduce a method based on persistent homology to automatically cluster the dataset of precomputed solutions to obtain different candidate initial guesses. We then train a Mixture-of-Experts within each cluster to predict initial guesses and provide a comparison with modality-agnostic learning. We demonstrate our method on a cart-pole toy problem and a quadrotor avoiding obstacles, and show that clustering samples based on inherent structure improves the warm-start quality.