Co-Designing Robots by Differentiating Motion Solvers

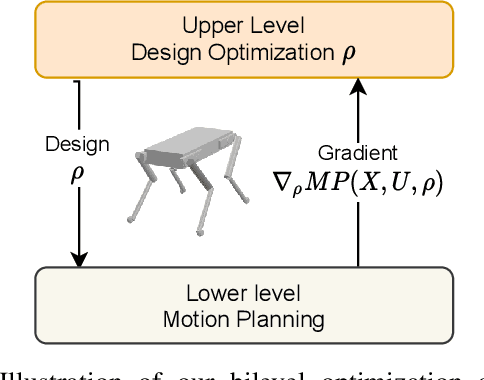
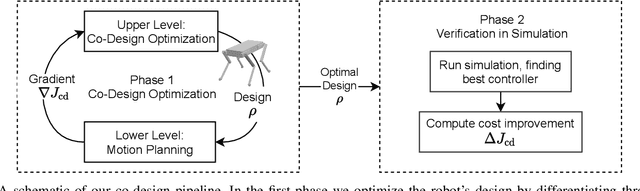
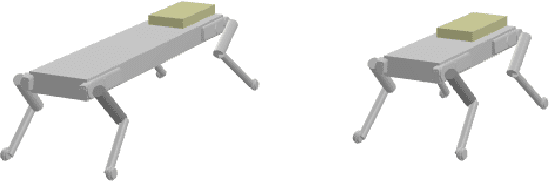
We present a novel algorithm for the computational co-design of legged robots and dynamic maneuvers. Current state-of-the-art approaches are based on random sampling or concurrent optimization. A few recently proposed methods explore the relationship between the gradient of the optimal motion and robot design. Inspired by these approaches, we propose a bilevel optimization approach that exploits the derivatives of the motion planning sub-problem (the inner level) without simplifying assumptions on its structure. Our approach can quickly optimize the robot's morphology while considering its full dynamics, joint limits and physical constraints such as friction cones. It has a faster convergence rate and greater scalability for larger design problems than state-of-the-art approaches based on sampling methods. It also allows us to handle constraints such as the actuation limits, which are important for co-designing dynamic maneuvers. We demonstrate these capabilities by studying jumping and trotting gaits under different design metrics and verify our results in a physics simulator. For these cases, our algorithm converges in less than a third of the number of iterations needed for sampling approaches, and the computation time scales linearly.