Dynamic Likelihood-free Inference via Ratio Estimation (DIRE)
Paper and Code
Oct 23, 2018


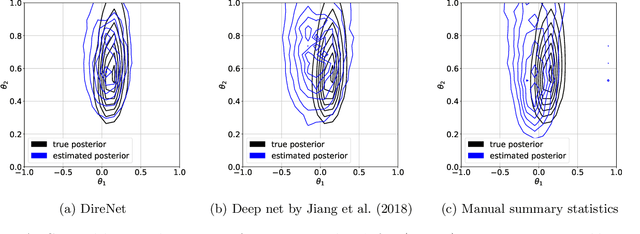
Parametric statistical models that are implicitly defined in terms of a stochastic data generating process are used in a wide range of scientific disciplines because they enable accurate modeling. However, learning the parameters from observed data is generally very difficult because their likelihood function is typically intractable. Likelihood-free Bayesian inference methods have been proposed which include the frameworks of approximate Bayesian computation (ABC), synthetic likelihood, and its recent generalization that performs likelihood-free inference by ratio estimation (LFIRE). A major difficulty in all these methods is choosing summary statistics that reduce the dimensionality of the data to facilitate inference. While several methods for choosing summary statistics have been proposed for ABC, the literature for synthetic likelihood and LFIRE is very thin to date. We here address this gap in the literature, focusing on the important special case of time-series models. We show that convolutional neural networks trained to predict the input parameters from the data provide suitable summary statistics for LFIRE. On a wide range of time-series models, a single neural network architecture produced equally or more accurate posteriors than alternative methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge