QuantFormer: Learning to Quantize for Neural Activity Forecasting in Mouse Visual Cortex

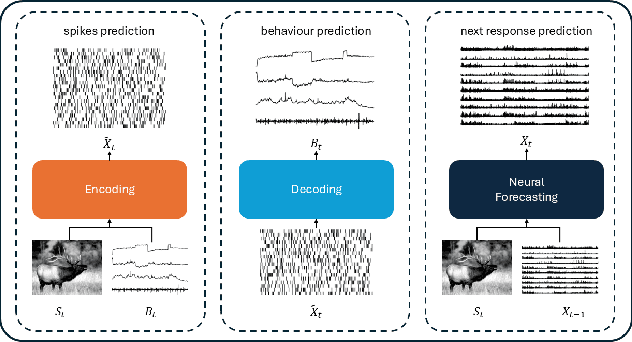
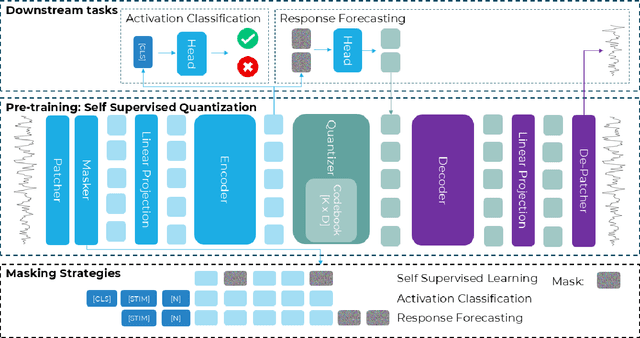
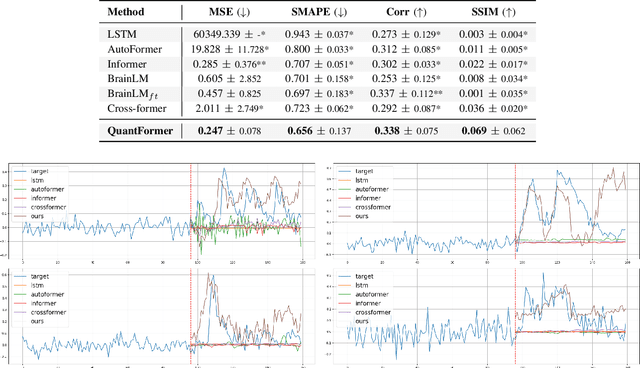
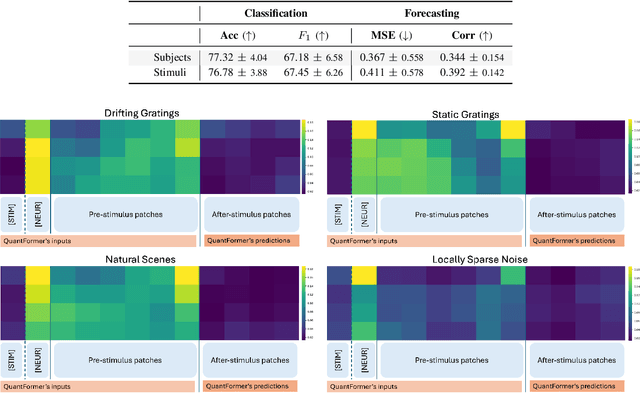
Understanding complex animal behaviors hinges on deciphering the neural activity patterns within brain circuits, making the ability to forecast neural activity crucial for developing predictive models of brain dynamics. This capability holds immense value for neuroscience, particularly in applications such as real-time optogenetic interventions. While traditional encoding and decoding methods have been used to map external variables to neural activity and vice versa, they focus on interpreting past data. In contrast, neural forecasting aims to predict future neural activity, presenting a unique and challenging task due to the spatiotemporal sparsity and complex dependencies of neural signals. Existing transformer-based forecasting methods, while effective in many domains, struggle to capture the distinctiveness of neural signals characterized by spatiotemporal sparsity and intricate dependencies. To address this challenge, we here introduce QuantFormer, a transformer-based model specifically designed for forecasting neural activity from two-photon calcium imaging data. Unlike conventional regression-based approaches, QuantFormerreframes the forecasting task as a classification problem via dynamic signal quantization, enabling more effective learning of sparse neural activation patterns. Additionally, QuantFormer tackles the challenge of analyzing multivariate signals from an arbitrary number of neurons by incorporating neuron-specific tokens, allowing scalability across diverse neuronal populations. Trained with unsupervised quantization on the Allen dataset, QuantFormer sets a new benchmark in forecasting mouse visual cortex activity. It demonstrates robust performance and generalization across various stimuli and individuals, paving the way for a foundational model in neural signal prediction.

Neural Conditional Probability for Inference

We introduce NCP (Neural Conditional Probability), a novel operator-theoretic approach for learning conditional distributions with a particular focus on inference tasks. NCP can be used to build conditional confidence regions and extract important statistics like conditional quantiles, mean, and covariance. It offers streamlined learning through a single unconditional training phase, facilitating efficient inference without the need for retraining even when conditioning changes. By tapping into the powerful approximation capabilities of neural networks, our method efficiently handles a wide variety of complex probability distributions, effectively dealing with nonlinear relationships between input and output variables. Theoretical guarantees ensure both optimization consistency and statistical accuracy of the NCP method. Our experiments show that our approach matches or beats leading methods using a simple Multi-Layer Perceptron (MLP) with two hidden layers and GELU activations. This demonstrates that a minimalistic architecture with a theoretically grounded loss function can achieve competitive results without sacrificing performance, even in the face of more complex architectures.

A randomized algorithm to solve reduced rank operator regression

We present and analyze an algorithm designed for addressing vector-valued regression problems involving possibly infinite-dimensional input and output spaces. The algorithm is a randomized adaptation of reduced rank regression, a technique to optimally learn a low-rank vector-valued function (i.e. an operator) between sampled data via regularized empirical risk minimization with rank constraints. We propose Gaussian sketching techniques both for the primal and dual optimization objectives, yielding Randomized Reduced Rank Regression (R4) estimators that are efficient and accurate. For each of our R4 algorithms we prove that the resulting regularized empirical risk is, in expectation w.r.t. randomness of a sketch, arbitrarily close to the optimal value when hyper-parameteres are properly tuned. Numerical expreriments illustrate the tightness of our bounds and show advantages in two distinct scenarios: (i) solving a vector-valued regression problem using synthetic and large-scale neuroscience datasets, and (ii) regressing the Koopman operator of a nonlinear stochastic dynamical system.