An Empirical Bernstein Inequality for Dependent Data in Hilbert Spaces and Applications

Learning from non-independent and non-identically distributed data poses a persistent challenge in statistical learning. In this study, we introduce data-dependent Bernstein inequalities tailored for vector-valued processes in Hilbert space. Our inequalities apply to both stationary and non-stationary processes and exploit the potential rapid decay of correlations between temporally separated variables to improve estimation. We demonstrate the utility of these bounds by applying them to covariance operator estimation in the Hilbert-Schmidt norm and to operator learning in dynamical systems, achieving novel risk bounds. Finally, we perform numerical experiments to illustrate the practical implications of these bounds in both contexts.

Demystifying Spectral Feature Learning for Instrumental Variable Regression

We address the problem of causal effect estimation in the presence of hidden confounders, using nonparametric instrumental variable (IV) regression. A leading strategy employs spectral features - that is, learned features spanning the top eigensubspaces of the operator linking treatments to instruments. We derive a generalization error bound for a two-stage least squares estimator based on spectral features, and gain insights into the method's performance and failure modes. We show that performance depends on two key factors, leading to a clear taxonomy of outcomes. In a good scenario, the approach is optimal. This occurs with strong spectral alignment, meaning the structural function is well-represented by the top eigenfunctions of the conditional operator, coupled with this operator's slow eigenvalue decay, indicating a strong instrument. Performance degrades in a bad scenario: spectral alignment remains strong, but rapid eigenvalue decay (indicating a weaker instrument) demands significantly more samples for effective feature learning. Finally, in the ugly scenario, weak spectral alignment causes the method to fail, regardless of the eigenvalues' characteristics. Our synthetic experiments empirically validate this taxonomy.

QuantFormer: Learning to Quantize for Neural Activity Forecasting in Mouse Visual Cortex

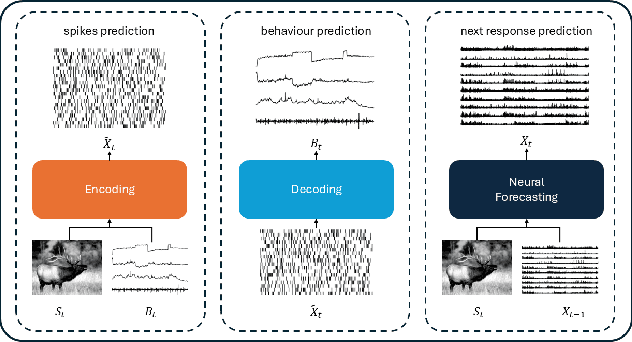
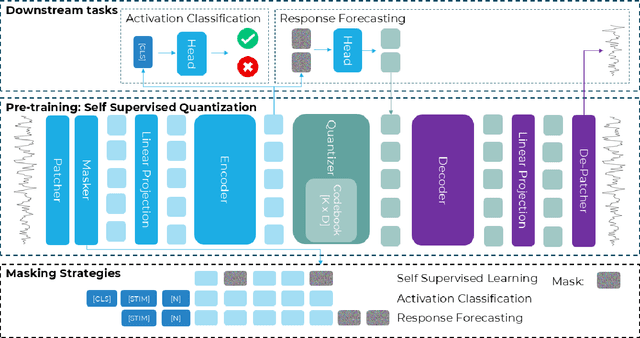
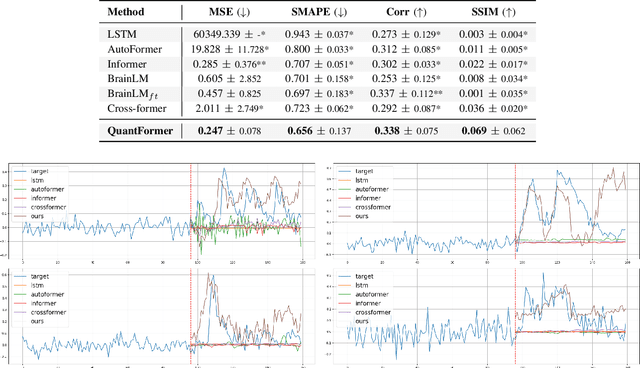
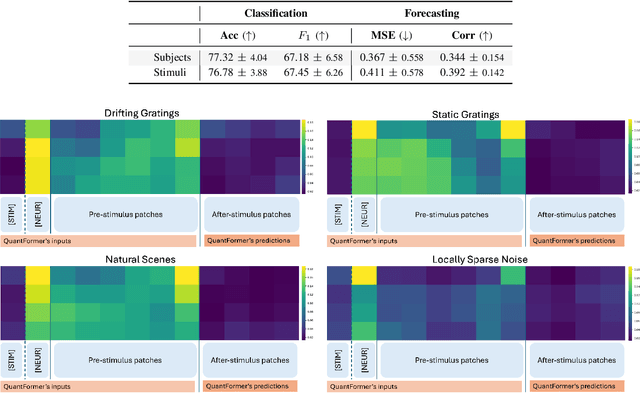
Understanding complex animal behaviors hinges on deciphering the neural activity patterns within brain circuits, making the ability to forecast neural activity crucial for developing predictive models of brain dynamics. This capability holds immense value for neuroscience, particularly in applications such as real-time optogenetic interventions. While traditional encoding and decoding methods have been used to map external variables to neural activity and vice versa, they focus on interpreting past data. In contrast, neural forecasting aims to predict future neural activity, presenting a unique and challenging task due to the spatiotemporal sparsity and complex dependencies of neural signals. Existing transformer-based forecasting methods, while effective in many domains, struggle to capture the distinctiveness of neural signals characterized by spatiotemporal sparsity and intricate dependencies. To address this challenge, we here introduce QuantFormer, a transformer-based model specifically designed for forecasting neural activity from two-photon calcium imaging data. Unlike conventional regression-based approaches, QuantFormerreframes the forecasting task as a classification problem via dynamic signal quantization, enabling more effective learning of sparse neural activation patterns. Additionally, QuantFormer tackles the challenge of analyzing multivariate signals from an arbitrary number of neurons by incorporating neuron-specific tokens, allowing scalability across diverse neuronal populations. Trained with unsupervised quantization on the Allen dataset, QuantFormer sets a new benchmark in forecasting mouse visual cortex activity. It demonstrates robust performance and generalization across various stimuli and individuals, paving the way for a foundational model in neural signal prediction.

Laplace Transform Based Low-Complexity Learning of Continuous Markov Semigroups

Markov processes serve as a universal model for many real-world random processes. This paper presents a data-driven approach for learning these models through the spectral decomposition of the infinitesimal generator (IG) of the Markov semigroup. The unbounded nature of IGs complicates traditional methods such as vector-valued regression and Hilbert-Schmidt operator analysis. Existing techniques, including physics-informed kernel regression, are computationally expensive and limited in scope, with no recovery guarantees for transfer operator methods when the time-lag is small. We propose a novel method that leverages the IG's resolvent, characterized by the Laplace transform of transfer operators. This approach is robust to time-lag variations, ensuring accurate eigenvalue learning even for small time-lags. Our statistical analysis applies to a broader class of Markov processes than current methods while reducing computational complexity from quadratic to linear in the state dimension. Finally, we illustrate the behaviour of our method in two experiments.

Neural Conditional Probability for Inference

We introduce NCP (Neural Conditional Probability), a novel operator-theoretic approach for learning conditional distributions with a particular focus on inference tasks. NCP can be used to build conditional confidence regions and extract important statistics like conditional quantiles, mean, and covariance. It offers streamlined learning through a single unconditional training phase, facilitating efficient inference without the need for retraining even when conditioning changes. By tapping into the powerful approximation capabilities of neural networks, our method efficiently handles a wide variety of complex probability distributions, effectively dealing with nonlinear relationships between input and output variables. Theoretical guarantees ensure both optimization consistency and statistical accuracy of the NCP method. Our experiments show that our approach matches or beats leading methods using a simple Multi-Layer Perceptron (MLP) with two hidden layers and GELU activations. This demonstrates that a minimalistic architecture with a theoretically grounded loss function can achieve competitive results without sacrificing performance, even in the face of more complex architectures.

Learning the Infinitesimal Generator of Stochastic Diffusion Processes

We address data-driven learning of the infinitesimal generator of stochastic diffusion processes, essential for understanding numerical simulations of natural and physical systems. The unbounded nature of the generator poses significant challenges, rendering conventional analysis techniques for Hilbert-Schmidt operators ineffective. To overcome this, we introduce a novel framework based on the energy functional for these stochastic processes. Our approach integrates physical priors through an energy-based risk metric in both full and partial knowledge settings. We evaluate the statistical performance of a reduced-rank estimator in reproducing kernel Hilbert spaces (RKHS) in the partial knowledge setting. Notably, our approach provides learning bounds independent of the state space dimension and ensures non-spurious spectral estimation. Additionally, we elucidate how the distortion between the intrinsic energy-induced metric of the stochastic diffusion and the RKHS metric used for generator estimation impacts the spectral learning bounds.

Deep projection networks for learning time-homogeneous dynamical systems

We consider the general class of time-homogeneous dynamical systems, both discrete and continuous, and study the problem of learning a meaningful representation of the state from observed data. This is instrumental for the task of learning a forward transfer operator of the system, that in turn can be used for forecasting future states or observables. The representation, typically parametrized via a neural network, is associated with a projection operator and is learned by optimizing an objective function akin to that of canonical correlation analysis (CCA). However, unlike CCA, our objective avoids matrix inversions and therefore is generally more stable and applicable to challenging scenarios. Our objective is a tight relaxation of CCA and we further enhance it by proposing two regularization schemes, one encouraging the orthogonality of the components of the representation while the other exploiting Chapman-Kolmogorov's equation. We apply our method to challenging discrete dynamical systems, discussing improvements over previous methods, as well as to continuous dynamical systems.

Estimating Koopman operators with sketching to provably learn large scale dynamical systems

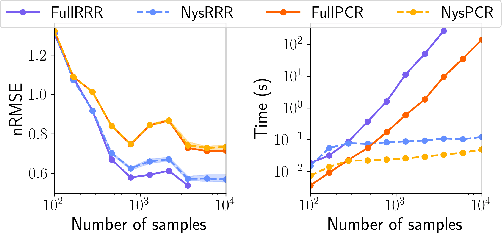
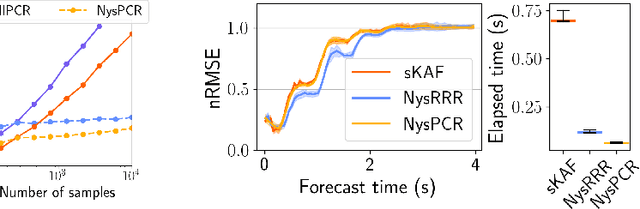
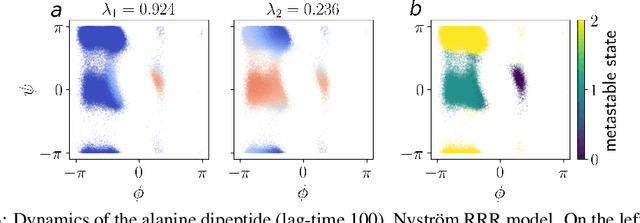
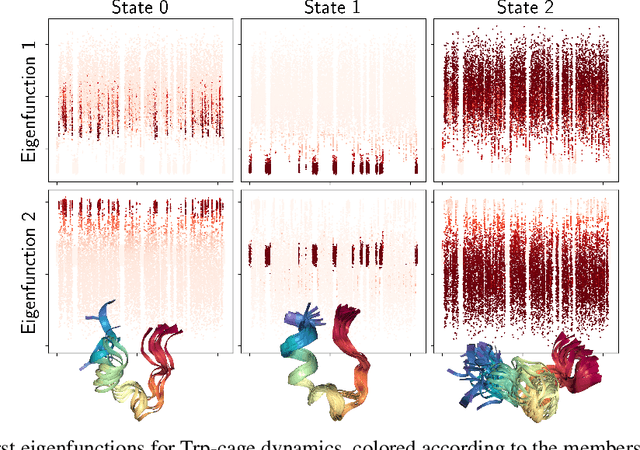
The theory of Koopman operators allows to deploy non-parametric machine learning algorithms to predict and analyze complex dynamical systems. Estimators such as principal component regression (PCR) or reduced rank regression (RRR) in kernel spaces can be shown to provably learn Koopman operators from finite empirical observations of the system's time evolution. Scaling these approaches to very long trajectories is a challenge and requires introducing suitable approximations to make computations feasible. In this paper, we boost the efficiency of different kernel-based Koopman operator estimators using random projections (sketching). We derive, implement and test the new "sketched" estimators with extensive experiments on synthetic and large-scale molecular dynamics datasets. Further, we establish non asymptotic error bounds giving a sharp characterization of the trade-offs between statistical learning rates and computational efficiency. Our empirical and theoretical analysis shows that the proposed estimators provide a sound and efficient way to learn large scale dynamical systems. In particular our experiments indicate that the proposed estimators retain the same accuracy of PCR or RRR, while being much faster.