Laplace Transform Based Low-Complexity Learning of Continuous Markov Semigroups

Markov processes serve as a universal model for many real-world random processes. This paper presents a data-driven approach for learning these models through the spectral decomposition of the infinitesimal generator (IG) of the Markov semigroup. The unbounded nature of IGs complicates traditional methods such as vector-valued regression and Hilbert-Schmidt operator analysis. Existing techniques, including physics-informed kernel regression, are computationally expensive and limited in scope, with no recovery guarantees for transfer operator methods when the time-lag is small. We propose a novel method that leverages the IG's resolvent, characterized by the Laplace transform of transfer operators. This approach is robust to time-lag variations, ensuring accurate eigenvalue learning even for small time-lags. Our statistical analysis applies to a broader class of Markov processes than current methods while reducing computational complexity from quadratic to linear in the state dimension. Finally, we illustrate the behaviour of our method in two experiments.

Multi-Source and Test-Time Domain Adaptation on Multivariate Signals using Spatio-Temporal Monge Alignment

Machine learning applications on signals such as computer vision or biomedical data often face significant challenges due to the variability that exists across hardware devices or session recordings. This variability poses a Domain Adaptation (DA) problem, as training and testing data distributions often differ. In this work, we propose Spatio-Temporal Monge Alignment (STMA) to mitigate these variabilities. This Optimal Transport (OT) based method adapts the cross-power spectrum density (cross-PSD) of multivariate signals by mapping them to the Wasserstein barycenter of source domains (multi-source DA). Predictions for new domains can be done with a filtering without the need for retraining a model with source data (test-time DA). We also study and discuss two special cases of the method, Temporal Monge Alignment (TMA) and Spatial Monge Alignment (SMA). Non-asymptotic concentration bounds are derived for the mappings estimation, which reveals a bias-plus-variance error structure with a variance decay rate of $\mathcal{O}(n_\ell^{-1/2})$ with $n_\ell$ the signal length. This theoretical guarantee demonstrates the efficiency of the proposed computational schema. Numerical experiments on multivariate biosignals and image data show that STMA leads to significant and consistent performance gains between datasets acquired with very different settings. Notably, STMA is a pre-processing step complementary to state-of-the-art deep learning methods.

Neural Conditional Probability for Inference

We introduce NCP (Neural Conditional Probability), a novel operator-theoretic approach for learning conditional distributions with a particular focus on inference tasks. NCP can be used to build conditional confidence regions and extract important statistics like conditional quantiles, mean, and covariance. It offers streamlined learning through a single unconditional training phase, facilitating efficient inference without the need for retraining even when conditioning changes. By tapping into the powerful approximation capabilities of neural networks, our method efficiently handles a wide variety of complex probability distributions, effectively dealing with nonlinear relationships between input and output variables. Theoretical guarantees ensure both optimization consistency and statistical accuracy of the NCP method. Our experiments show that our approach matches or beats leading methods using a simple Multi-Layer Perceptron (MLP) with two hidden layers and GELU activations. This demonstrates that a minimalistic architecture with a theoretically grounded loss function can achieve competitive results without sacrificing performance, even in the face of more complex architectures.

Contextual Continuum Bandits: Static Versus Dynamic Regret

We study the contextual continuum bandits problem, where the learner sequentially receives a side information vector and has to choose an action in a convex set, minimizing a function associated to the context. The goal is to minimize all the underlying functions for the received contexts, leading to a dynamic (contextual) notion of regret, which is stronger than the standard static regret. Assuming that the objective functions are H\"older with respect to the contexts, we demonstrate that any algorithm achieving a sub-linear static regret can be extended to achieve a sub-linear dynamic regret. We further study the case of strongly convex and smooth functions when the observations are noisy. Inspired by the interior point method and employing self-concordant barriers, we propose an algorithm achieving a sub-linear dynamic regret. Lastly, we present a minimax lower bound, implying two key facts. First, no algorithm can achieve sub-linear dynamic regret over functions that are not continuous with respect to the context. Second, for strongly convex and smooth functions, the algorithm that we propose achieves, up to a logarithmic factor, the minimax optimal rate of dynamic regret as a function of the number of queries.

Learning the Infinitesimal Generator of Stochastic Diffusion Processes

We address data-driven learning of the infinitesimal generator of stochastic diffusion processes, essential for understanding numerical simulations of natural and physical systems. The unbounded nature of the generator poses significant challenges, rendering conventional analysis techniques for Hilbert-Schmidt operators ineffective. To overcome this, we introduce a novel framework based on the energy functional for these stochastic processes. Our approach integrates physical priors through an energy-based risk metric in both full and partial knowledge settings. We evaluate the statistical performance of a reduced-rank estimator in reproducing kernel Hilbert spaces (RKHS) in the partial knowledge setting. Notably, our approach provides learning bounds independent of the state space dimension and ensures non-spurious spectral estimation. Additionally, we elucidate how the distortion between the intrinsic energy-induced metric of the stochastic diffusion and the RKHS metric used for generator estimation impacts the spectral learning bounds.

Consistent Long-Term Forecasting of Ergodic Dynamical Systems

We study the evolution of distributions under the action of an ergodic dynamical system, which may be stochastic in nature. By employing tools from Koopman and transfer operator theory one can evolve any initial distribution of the state forward in time, and we investigate how estimators of these operators perform on long-term forecasting. Motivated by the observation that standard estimators may fail at this task, we introduce a learning paradigm that neatly combines classical techniques of eigenvalue deflation from operator theory and feature centering from statistics. This paradigm applies to any operator estimator based on empirical risk minimization, making them satisfy learning bounds which hold uniformly on the entire trajectory of future distributions, and abide to the conservation of mass for each of the forecasted distributions. Numerical experiments illustrates the advantages of our approach in practice.

Deep projection networks for learning time-homogeneous dynamical systems

We consider the general class of time-homogeneous dynamical systems, both discrete and continuous, and study the problem of learning a meaningful representation of the state from observed data. This is instrumental for the task of learning a forward transfer operator of the system, that in turn can be used for forecasting future states or observables. The representation, typically parametrized via a neural network, is associated with a projection operator and is learned by optimizing an objective function akin to that of canonical correlation analysis (CCA). However, unlike CCA, our objective avoids matrix inversions and therefore is generally more stable and applicable to challenging scenarios. Our objective is a tight relaxation of CCA and we further enhance it by proposing two regularization schemes, one encouraging the orthogonality of the components of the representation while the other exploiting Chapman-Kolmogorov's equation. We apply our method to challenging discrete dynamical systems, discussing improvements over previous methods, as well as to continuous dynamical systems.

Koopman Operator Learning: Sharp Spectral Rates and Spurious Eigenvalues

Non-linear dynamical systems can be handily described by the associated Koopman operator, whose action evolves every observable of the system forward in time. Learning the Koopman operator from data is enabled by a number of algorithms. In this work we present nonasymptotic learning bounds for the Koopman eigenvalues and eigenfunctions estimated by two popular algorithms: Extended Dynamic Mode Decomposition (EDMD) and Reduced Rank Regression (RRR). We focus on time-reversal-invariant Markov chains, implying that the Koopman operator is self-adjoint. This includes important examples of stochastic dynamical systems, notably Langevin dynamics. Our spectral learning bounds are driven by the simultaneous control of the operator norm risk of the estimators and a metric distortion associated to the corresponding eigenfunctions. Our analysis indicates that both algorithms have similar variance, but EDMD suffers from a larger bias which might be detrimental to its learning rate. We further argue that a large metric distortion may lead to spurious eigenvalues, a phenomenon which has been empirically observed, and note that metric distortion can be estimated from data. Numerical experiments complement the theoretical findings.

Meta Representation Learning with Contextual Linear Bandits

Meta-learning seeks to build algorithms that rapidly learn how to solve new learning problems based on previous experience. In this paper we investigate meta-learning in the setting of stochastic linear bandit tasks. We assume that the tasks share a low dimensional representation, which has been partially acquired from previous learning tasks. We aim to leverage this information in order to learn a new downstream bandit task, which shares the same representation. Our principal contribution is to show that if the learned representation estimates well the unknown one, then the downstream task can be efficiently learned by a greedy policy that we propose in this work. We derive an upper bound on the regret of this policy, which is, up to logarithmic factors, of order $r\sqrt{N}(1\vee \sqrt{d/T})$, where $N$ is the horizon of the downstream task, $T$ is the number of training tasks, $d$ the ambient dimension and $r \ll d$ the dimension of the representation. We highlight that our strategy does not need to know $r$. We note that if $T> d$ our bound achieves the same rate of optimal minimax bandit algorithms using the true underlying representation. Our analysis is inspired and builds in part upon previous work on meta-learning in the i.i.d. full information setting \citep{tripuraneni2021provable,boursier2022trace}. As a separate contribution we show how to relax certain assumptions in those works, thereby improving their representation learning and risk analysis.

AdaCap: Adaptive Capacity control for Feed-Forward Neural Networks

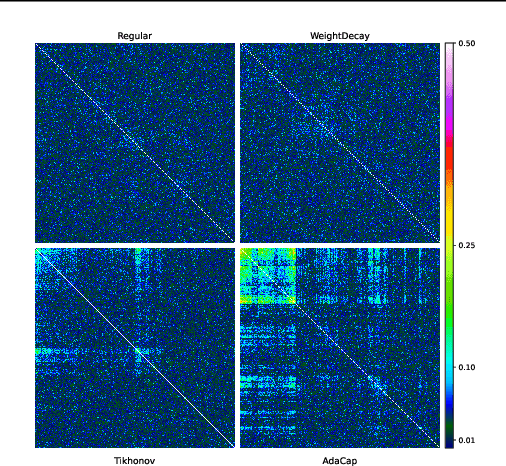
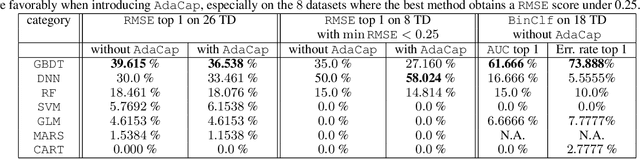
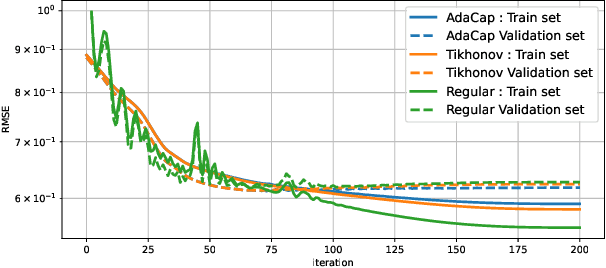
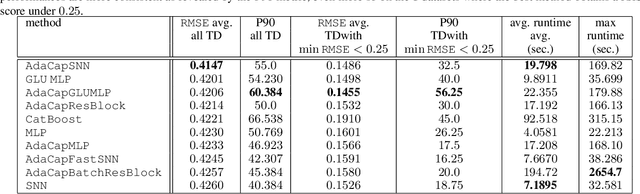
The capacity of a ML model refers to the range of functions this model can approximate. It impacts both the complexity of the patterns a model can learn but also memorization, the ability of a model to fit arbitrary labels. We propose Adaptive Capacity (AdaCap), a training scheme for Feed-Forward Neural Networks (FFNN). AdaCap optimizes the capacity of FFNN so it can capture the high-level abstract representations underlying the problem at hand without memorizing the training dataset. AdaCap is the combination of two novel ingredients, the Muddling labels for Regularization (MLR) loss and the Tikhonov operator training scheme. The MLR loss leverages randomly generated labels to quantify the propensity of a model to memorize. We prove that the MLR loss is an accurate in-sample estimator for out-of-sample generalization performance and that it can be used to perform Hyper-Parameter Optimization provided a Signal-to-Noise Ratio condition is met. The Tikhonov operator training scheme modulates the capacity of a FFNN in an adaptive, differentiable and data-dependent manner. We assess the effectiveness of AdaCap in a setting where DNN are typically prone to memorization, small tabular datasets, and benchmark its performance against popular machine learning methods.