AdaCap: Adaptive Capacity control for Feed-Forward Neural Networks

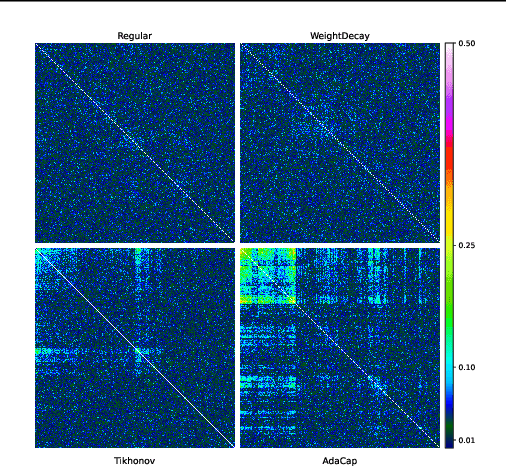
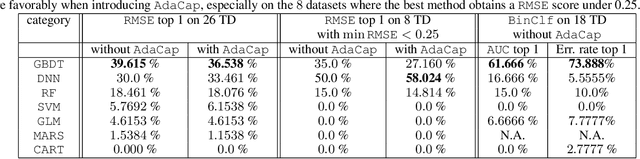
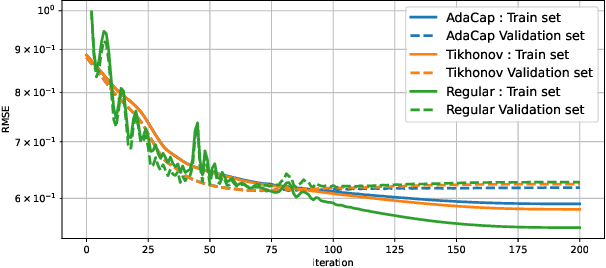
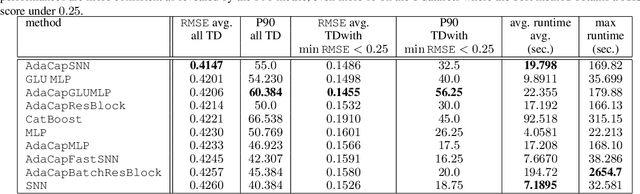
The capacity of a ML model refers to the range of functions this model can approximate. It impacts both the complexity of the patterns a model can learn but also memorization, the ability of a model to fit arbitrary labels. We propose Adaptive Capacity (AdaCap), a training scheme for Feed-Forward Neural Networks (FFNN). AdaCap optimizes the capacity of FFNN so it can capture the high-level abstract representations underlying the problem at hand without memorizing the training dataset. AdaCap is the combination of two novel ingredients, the Muddling labels for Regularization (MLR) loss and the Tikhonov operator training scheme. The MLR loss leverages randomly generated labels to quantify the propensity of a model to memorize. We prove that the MLR loss is an accurate in-sample estimator for out-of-sample generalization performance and that it can be used to perform Hyper-Parameter Optimization provided a Signal-to-Noise Ratio condition is met. The Tikhonov operator training scheme modulates the capacity of a FFNN in an adaptive, differentiable and data-dependent manner. We assess the effectiveness of AdaCap in a setting where DNN are typically prone to memorization, small tabular datasets, and benchmark its performance against popular machine learning methods.

Muddling Label Regularization: Deep Learning for Tabular Datasets

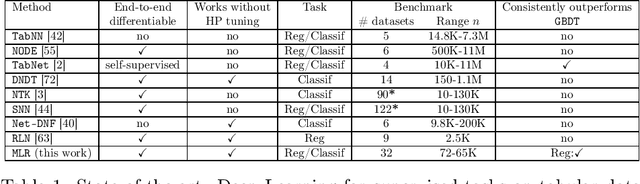
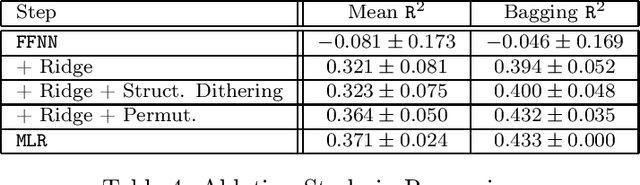
Deep Learning (DL) is considered the state-of-the-art in computer vision, speech recognition and natural language processing. Until recently, it was also widely accepted that DL is irrelevant for learning tasks on tabular data, especially in the small sample regime where ensemble methods are acknowledged as the gold standard. We present a new end-to-end differentiable method to train a standard FFNN. Our method, \textbf{Muddling labels for Regularization} (\texttt{MLR}), penalizes memorization through the generation of uninformative labels and the application of a differentiable close-form regularization scheme on the last hidden layer during training. \texttt{MLR} outperforms classical NN and the gold standard (GBDT, RF) for regression and classification tasks on several datasets from the UCI database and Kaggle covering a large range of sample sizes and feature to sample ratios. Researchers and practitioners can use \texttt{MLR} on its own as an off-the-shelf \DL{} solution or integrate it into the most advanced ML pipelines.

Muddling Labels for Regularization, a novel approach to generalization

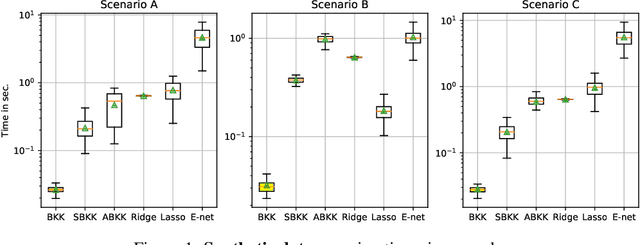
Generalization is a central problem in Machine Learning. Indeed most prediction methods require careful calibration of hyperparameters usually carried out on a hold-out \textit{validation} dataset to achieve generalization. The main goal of this paper is to introduce a novel approach to achieve generalization without any data splitting, which is based on a new risk measure which directly quantifies a model's tendency to overfit. To fully understand the intuition and advantages of this new approach, we illustrate it in the simple linear regression model ($Y=X\beta+\xi$) where we develop a new criterion. We highlight how this criterion is a good proxy for the true generalization risk. Next, we derive different procedures which tackle several structures simultaneously (correlation, sparsity,...). Noticeably, these procedures \textbf{concomitantly} train the model and calibrate the hyperparameters. In addition, these procedures can be implemented via classical gradient descent methods when the criterion is differentiable w.r.t. the hyperparameters. Our numerical experiments reveal that our procedures are computationally feasible and compare favorably to the popular approach (Ridge, LASSO and Elastic-Net combined with grid-search cross-validation) in term of generalization. They also outperform the baseline on two additional tasks: estimation and support recovery of $\beta$. Moreover, our procedures do not require any expertise for the calibration of the initial parameters which remain the same for all the datasets we experimented on.

Optimizing generalization on the train set: a novel gradient-based framework to train parameters and hyperparameters simultaneously

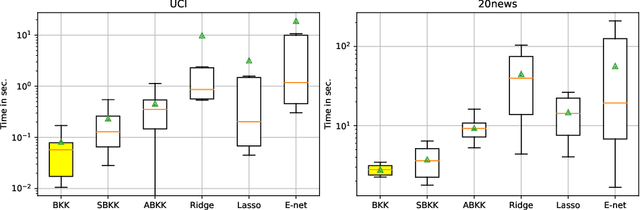
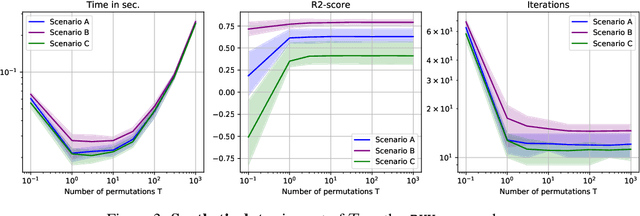
Generalization is a central problem in Machine Learning. Most prediction methods require careful calibration of hyperparameters carried out on a hold-out \textit{validation} dataset to achieve generalization. The main goal of this paper is to present a novel approach based on a new measure of risk that allows us to develop novel fully automatic procedures for generalization. We illustrate the pertinence of this new framework in the regression problem. The main advantages of this new approach are: (i) it can simultaneously train the model and perform regularization in a single run of a gradient-based optimizer on all available data without any previous hyperparameter tuning; (ii) this framework can tackle several additional objectives simultaneously (correlation, sparsity,...) $via$ the introduction of regularization parameters. Noticeably, our approach transforms hyperparameter tuning as well as feature selection (a combinatorial discrete optimization problem) into a continuous optimization problem that is solvable via classical gradient-based methods ; (iii) the computational complexity of our methods is $O(npK)$ where $n,p,K$ denote respectively the number of observations, features and iterations of the gradient descent algorithm. We observe in our experiments a significantly smaller runtime for our methods as compared to benchmark methods for equivalent prediction score. Our procedures are implemented in PyTorch (code is available for replication).