Optimizing generalization on the train set: a novel gradient-based framework to train parameters and hyperparameters simultaneously
Paper and Code
Jun 11, 2020
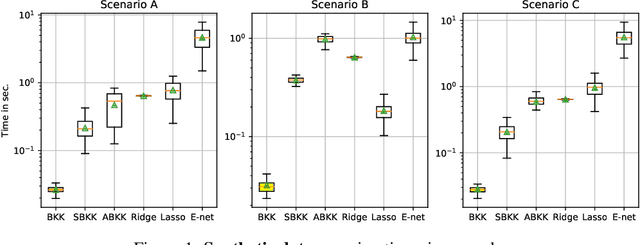
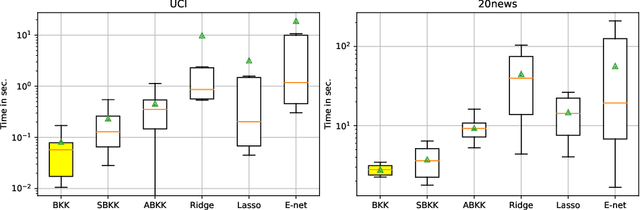
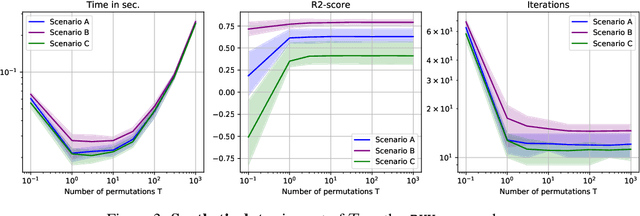
Generalization is a central problem in Machine Learning. Most prediction methods require careful calibration of hyperparameters carried out on a hold-out \textit{validation} dataset to achieve generalization. The main goal of this paper is to present a novel approach based on a new measure of risk that allows us to develop novel fully automatic procedures for generalization. We illustrate the pertinence of this new framework in the regression problem. The main advantages of this new approach are: (i) it can simultaneously train the model and perform regularization in a single run of a gradient-based optimizer on all available data without any previous hyperparameter tuning; (ii) this framework can tackle several additional objectives simultaneously (correlation, sparsity,...) $via$ the introduction of regularization parameters. Noticeably, our approach transforms hyperparameter tuning as well as feature selection (a combinatorial discrete optimization problem) into a continuous optimization problem that is solvable via classical gradient-based methods ; (iii) the computational complexity of our methods is $O(npK)$ where $n,p,K$ denote respectively the number of observations, features and iterations of the gradient descent algorithm. We observe in our experiments a significantly smaller runtime for our methods as compared to benchmark methods for equivalent prediction score. Our procedures are implemented in PyTorch (code is available for replication).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge