A Perturbation Resilient Framework for Unsupervised Learning

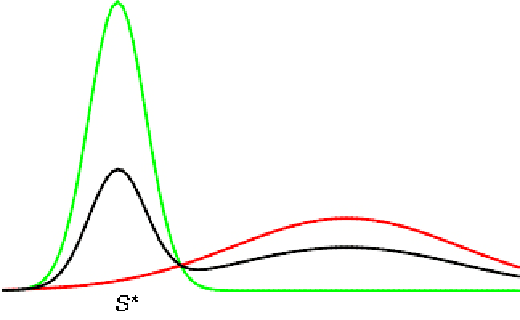
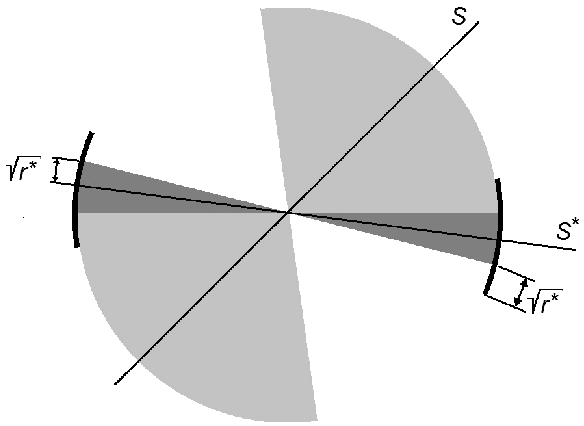
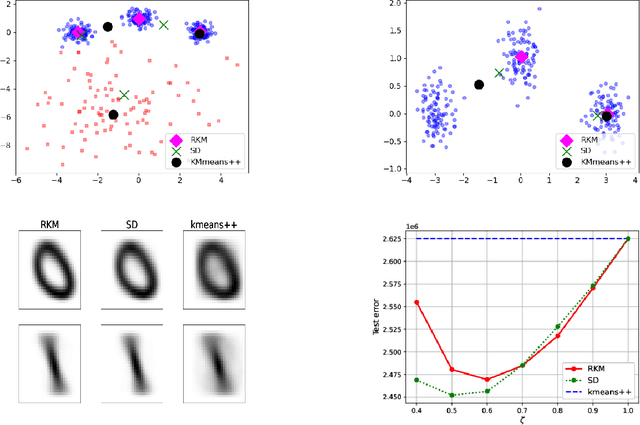
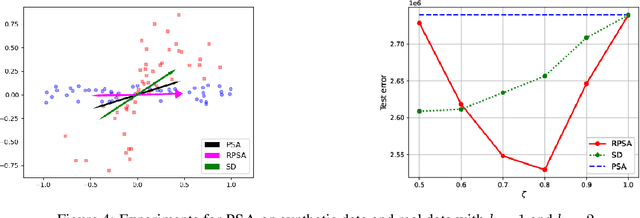
Designing learning algorithms that are resistant to perturbations of the underlying data distribution is a problem of wide practical and theoretical importance. We present a general approach to this problem focusing on unsupervised learning. The key assumption is that the perturbing distribution is characterized by larger losses relative to a given class of admissible models. This is exploited by a general descent algorithm which minimizes an $L$-statistic criterion over the model class, weighting more small losses. We characterize the robustness of the method in terms of bounds on the reconstruction error for the assumed unperturbed distribution. Numerical experiments with \textsc{kmeans} clustering and principal subspace analysis demonstrate the effectiveness of our method.