High Probability Bounds for Stochastic Subgradient Schemes with Heavy Tailed Noise

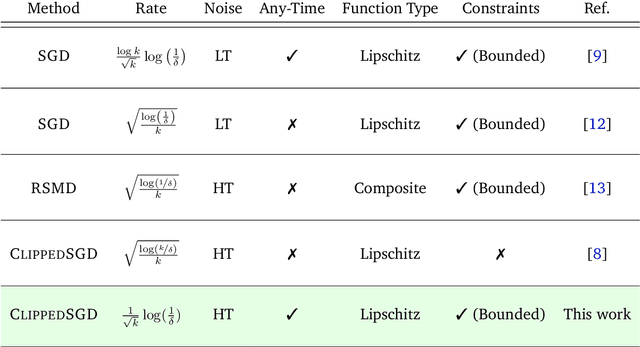
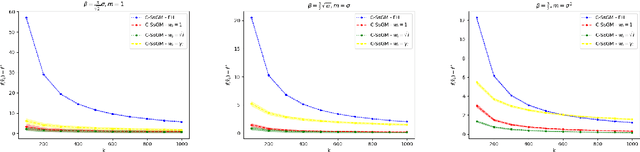
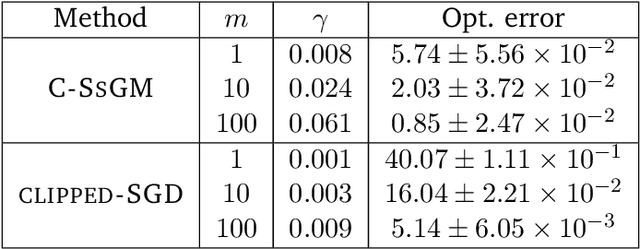
In this work we study high probability bounds for stochastic subgradient methods under heavy tailed noise. In this case the noise is only assumed to have finite variance as opposed to a sub-Gaussian distribution for which it is known that standard subgradient methods enjoys high probability bounds. We analyzed a clipped version of the projected stochastic subgradient method, where subgradient estimates are truncated whenever they have large norms. We show that this clipping strategy leads both to near optimal any-time and finite horizon bounds for many classical averaging schemes. Preliminary experiments are shown to support the validity of the method.

A Perturbation Resilient Framework for Unsupervised Learning

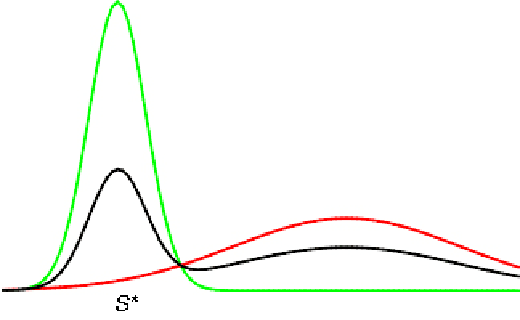
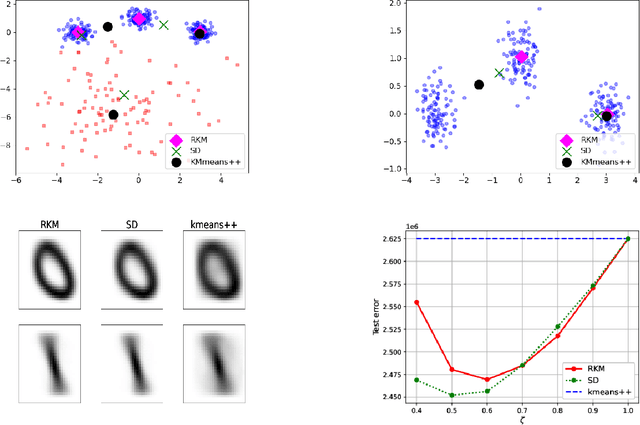
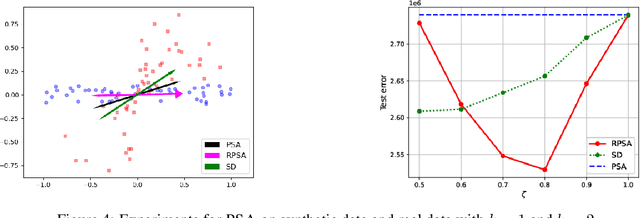
Designing learning algorithms that are resistant to perturbations of the underlying data distribution is a problem of wide practical and theoretical importance. We present a general approach to this problem focusing on unsupervised learning. The key assumption is that the perturbing distribution is characterized by larger losses relative to a given class of admissible models. This is exploited by a general descent algorithm which minimizes an $L$-statistic criterion over the model class, weighting more small losses. We characterize the robustness of the method in terms of bounds on the reconstruction error for the assumed unperturbed distribution. Numerical experiments with \textsc{kmeans} clustering and principal subspace analysis demonstrate the effectiveness of our method.