High Probability Bounds for Stochastic Subgradient Schemes with Heavy Tailed Noise
Paper and Code
Aug 17, 2022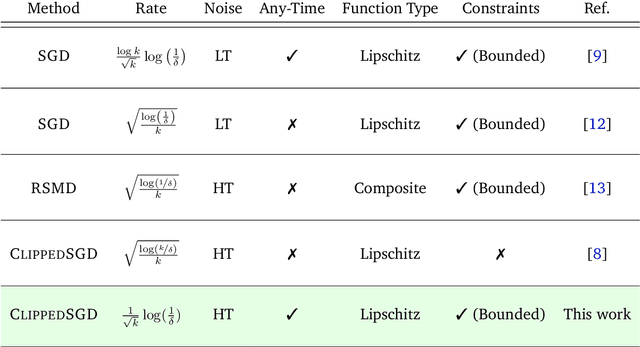
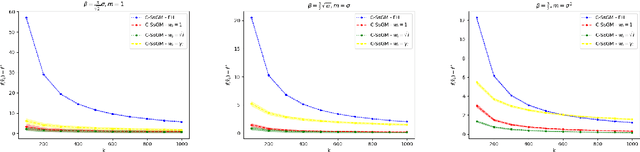
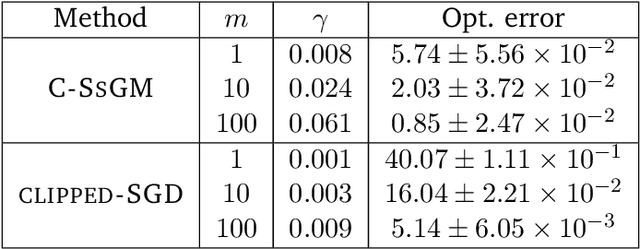
In this work we study high probability bounds for stochastic subgradient methods under heavy tailed noise. In this case the noise is only assumed to have finite variance as opposed to a sub-Gaussian distribution for which it is known that standard subgradient methods enjoys high probability bounds. We analyzed a clipped version of the projected stochastic subgradient method, where subgradient estimates are truncated whenever they have large norms. We show that this clipping strategy leads both to near optimal any-time and finite horizon bounds for many classical averaging schemes. Preliminary experiments are shown to support the validity of the method.
* 22 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge