Nonsmooth Implicit Differentiation: Deterministic and Stochastic Convergence Rates

We study the problem of efficiently computing the derivative of the fixed-point of a parametric nondifferentiable contraction map. This problem has wide applications in machine learning, including hyperparameter optimization, meta-learning and data poisoning attacks. We analyze two popular approaches: iterative differentiation (ITD) and approximate implicit differentiation (AID). A key challenge behind the nonsmooth setting is that the chain rule does not hold anymore. Building upon the recent work by Bolte et al. (2022), who proved linear convergence of nondifferentiable ITD, we provide an improved linear rate for ITD and a slightly better rate for AID, both in the deterministic case. We further introduce NSID, a new stochastic method to compute the implicit derivative when the fixed point is defined as the composition of an outer map and an inner map which is accessible only through a stochastic unbiased estimator. We establish rates for the convergence of NSID, encompassing the best available rates in the smooth setting. We present illustrative experiments confirming our analysis.

Relax and penalize: a new bilevel approach to mixed-binary hyperparameter optimization

In recent years, bilevel approaches have become very popular to efficiently estimate high-dimensional hyperparameters of machine learning models. However, to date, binary parameters are handled by continuous relaxation and rounding strategies, which could lead to inconsistent solutions. In this context, we tackle the challenging optimization of mixed-binary hyperparameters by resorting to an equivalent continuous bilevel reformulation based on an appropriate penalty term. We propose an algorithmic framework that, under suitable assumptions, is guaranteed to provide mixed-binary solutions. Moreover, the generality of the method allows to safely use existing continuous bilevel solvers within the proposed framework. We evaluate the performance of our approach for a specific machine learning problem, i.e., the estimation of the group-sparsity structure in regression problems. Reported results clearly show that our method outperforms state-of-the-art approaches based on relaxation and rounding

Variance reduction techniques for stochastic proximal point algorithms

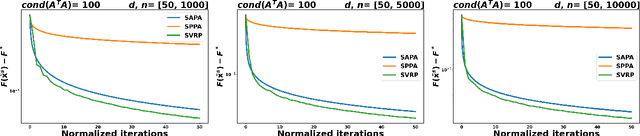
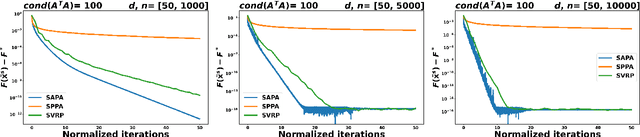
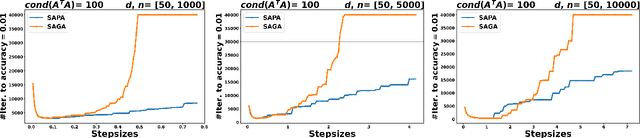
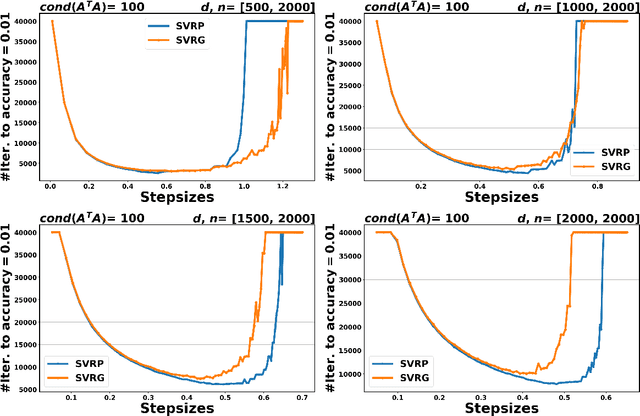
In the context of finite sums minimization, variance reduction techniques are widely used to improve the performance of state-of-the-art stochastic gradient methods. Their practical impact is clear, as well as their theoretical properties. Stochastic proximal point algorithms have been studied as an alternative to stochastic gradient algorithms since they are more stable with respect to the choice of the stepsize but a proper variance reduced version is missing. In this work, we propose the first study of variance reduction techniques for stochastic proximal point algorithms. We introduce a stochastic proximal version of SVRG, SAGA, and some of their variants for smooth and convex functions. We provide several convergence results for the iterates and the objective function values. In addition, under the Polyak-{\L}ojasiewicz (PL) condition, we obtain linear convergence rates for the iterates and the function values. Our numerical experiments demonstrate the advantages of the proximal variance reduction methods over their gradient counterparts, especially about the stability with respect to the choice of the step size.

High Probability Bounds for Stochastic Subgradient Schemes with Heavy Tailed Noise

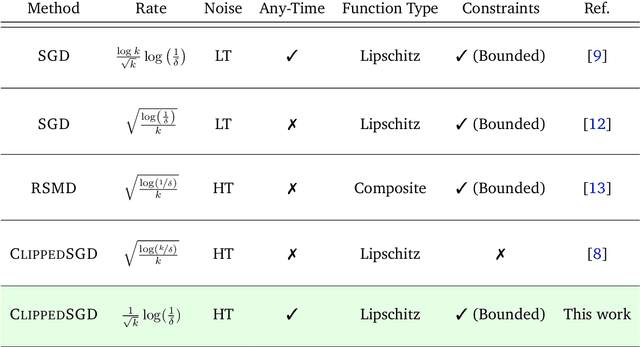
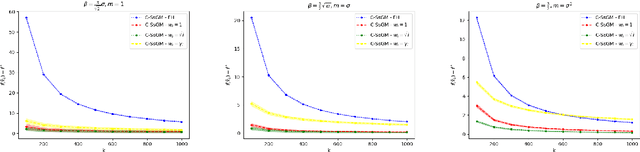
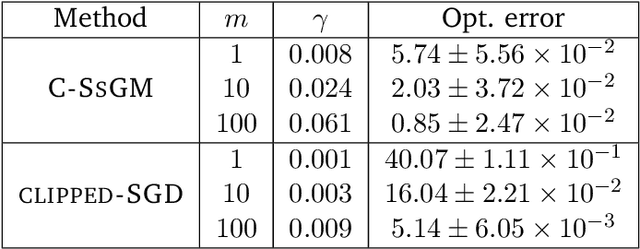
In this work we study high probability bounds for stochastic subgradient methods under heavy tailed noise. In this case the noise is only assumed to have finite variance as opposed to a sub-Gaussian distribution for which it is known that standard subgradient methods enjoys high probability bounds. We analyzed a clipped version of the projected stochastic subgradient method, where subgradient estimates are truncated whenever they have large norms. We show that this clipping strategy leads both to near optimal any-time and finite horizon bounds for many classical averaging schemes. Preliminary experiments are shown to support the validity of the method.

Bilevel Optimization with a Lower-level Contraction: Optimal Sample Complexity without Warm-Start

We analyze a general class of bilevel problems, in which the upper-level problem consists in the minimization of a smooth objective function and the lower-level problem is to find the fixed point of a smooth contraction map. This type of problems include instances of meta-learning, hyperparameter optimization and data poisoning adversarial attacks. Several recent works have proposed algorithms which warm-start the lower-level problem, i.e. they use the previous lower-level approximate solution as a staring point for the lower-level solver. This warm-start procedure allows one to improve the sample complexity in both the stochastic and deterministic settings, achieving in some cases the order-wise optimal sample complexity. We show that without warm-start, it is still possible to achieve order-wise optimal and near-optimal sample complexity for the stochastic and deterministic settings, respectively. In particular, we propose a simple method which uses stochastic fixed point iterations at the lower-level and projected inexact gradient descent at the upper-level, that reaches an $\epsilon$-stationary point using $O(\epsilon^{-2})$ and $\tilde{O}(\epsilon^{-1})$ samples for the stochastic and the deterministic setting, respectively. Compared to methods using warm-start, ours is better suited for meta-learning and yields a simpler analysis that does not need to study the coupled interactions between the upper-level and lower-level iterates.

Convergence of Batch Greenkhorn for Regularized Multimarginal Optimal Transport

In this work we propose a batch version of the Greenkhorn algorithm for multimarginal regularized optimal transport problems. Our framework is general enough to cover, as particular cases, some existing algorithms like Sinkhorn and Greenkhorn algorithm for the bi-marginal setting, and (greedy) MultiSinkhorn for multimarginal optimal transport. We provide a complete convergence analysis, which is based on the properties of the iterative Bregman projections (IBP) method with greedy control. Global linear rate of convergence and explicit bound on the iteration complexity are obtained. When specialized to above mentioned algorithms, our results give new insights and/or improve existing ones.

Convergence Properties of Stochastic Hypergradients

Bilevel optimization problems are receiving increasing attention in machine learning as they provide a natural framework for hyperparameter optimization and meta-learning. A key step to tackle these problems in the design of optimization algorithms for bilevel optimization is the efficient computation of the gradient of the upper-level objective (hypergradient). In this work, we study stochastic approximation schemes for the hypergradient, which are important when the lower-level problem is empirical risk minimization on a large dataset. We provide iteration complexity bounds for the mean square error of the hypergradient approximation, under the assumption that the lower-level problem is accessible only through a stochastic mapping which is a contraction in expectation. Preliminary numerical experiments support our theoretical analysis.

On the Iteration Complexity of Hypergradient Computation

We study a general class of bilevel problems, consisting in the minimization of an upper-level objective which depends on the solution to a parametric fixed-point equation. Important instances arising in machine learning include hyperparameter optimization, meta-learning, and certain graph and recurrent neural networks. Typically the gradient of the upper-level objective (hypergradient) is hard or even impossible to compute exactly, which has raised the interest in approximation methods. We investigate some popular approaches to compute the hypergradient, based on reverse mode iterative differentiation and approximate implicit differentiation. Under the hypothesis that the fixed point equation is defined by a contraction mapping, we present a unified analysis which allows for the first time to quantitatively compare these methods, providing explicit bounds for their iteration complexity. This analysis suggests a hierarchy in terms of computational efficiency among the above methods, with approximate implicit differentiation based on conjugate gradient performing best. We present an extensive experimental comparison among the methods which confirm the theoretical findings.

Efficient Tensor Kernel methods for sparse regression

Recently, classical kernel methods have been extended by the introduction of suitable tensor kernels so to promote sparsity in the solution of the underlying regression problem. Indeed, they solve an lp-norm regularization problem, with p=m/(m-1) and m even integer, which happens to be close to a lasso problem. However, a major drawback of the method is that storing tensors requires a considerable amount of memory, ultimately limiting its applicability. In this work we address this problem by proposing two advances. First, we directly reduce the memory requirement, by intriducing a new and more efficient layout for storing the data. Second, we use a Nystrom-type subsampling approach, which allows for a training phase with a smaller number of data points, so to reduce the computational cost. Experiments, both on synthetic and read datasets, show the effectiveness of the proposed improvements. Finally, we take case of implementing the cose in C++ so to further speed-up the computation.

Sinkhorn Barycenters with Free Support via Frank-Wolfe Algorithm

We present a novel algorithm to estimate the barycenter of arbitrary probability distributions with respect to the Sinkhorn divergence. Based on a Frank-Wolfe optimization strategy, our approach proceeds by populating the support of the barycenter incrementally, without requiring any pre-allocation. We consider discrete as well as continuous distributions, proving convergence rates of the proposed algorithm in both settings. Key elements of our analysis are a new result showing that the Sinkhorn divergence on compact domains has Lipschitz continuous gradient with respect to the Total Variation and a characterization of the sample complexity of Sinkhorn potentials. Experiments validate the effectiveness of our method in practice.