Jordan Frecon
LHC
Relax and penalize: a new bilevel approach to mixed-binary hyperparameter optimization
Aug 21, 2023Abstract:In recent years, bilevel approaches have become very popular to efficiently estimate high-dimensional hyperparameters of machine learning models. However, to date, binary parameters are handled by continuous relaxation and rounding strategies, which could lead to inconsistent solutions. In this context, we tackle the challenging optimization of mixed-binary hyperparameters by resorting to an equivalent continuous bilevel reformulation based on an appropriate penalty term. We propose an algorithmic framework that, under suitable assumptions, is guaranteed to provide mixed-binary solutions. Moreover, the generality of the method allows to safely use existing continuous bilevel solvers within the proposed framework. We evaluate the performance of our approach for a specific machine learning problem, i.e., the estimation of the group-sparsity structure in regression problems. Reported results clearly show that our method outperforms state-of-the-art approaches based on relaxation and rounding
Bayesian selection for the l2-Potts model regularization parameter: 1D piecewise constant signal denoising
Feb 27, 2017



Abstract:Piecewise constant denoising can be solved either by deterministic optimization approaches, based on the Potts model, or by stochastic Bayesian procedures. The former lead to low computational time but require the selection of a regularization parameter, whose value significantly impacts the achieved solution, and whose automated selection remains an involved and challenging problem. Conversely, fully Bayesian formalisms encapsulate the regularization parameter selection into hierarchical models, at the price of high computational costs. This contribution proposes an operational strategy that combines hierarchical Bayesian and Potts model formulations, with the double aim of automatically tuning the regularization parameter and of maintaining computational effciency. The proposed procedure relies on formally connecting a Bayesian framework to a l2-Potts functional. Behaviors and performance for the proposed piecewise constant denoising and regularization parameter tuning techniques are studied qualitatively and assessed quantitatively, and shown to compare favorably against those of a fully Bayesian hierarchical procedure, both in accuracy and in computational load.
On-the-fly Approximation of Multivariate Total Variation Minimization
Aug 28, 2016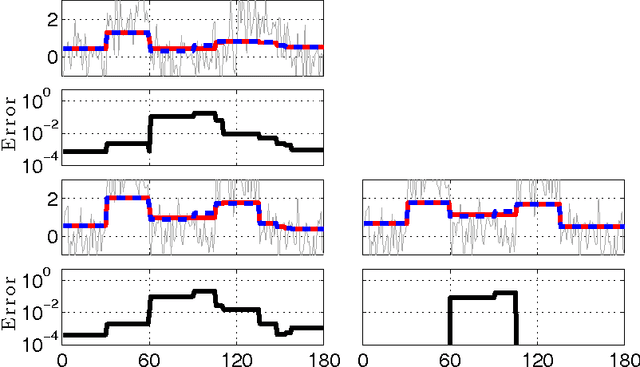
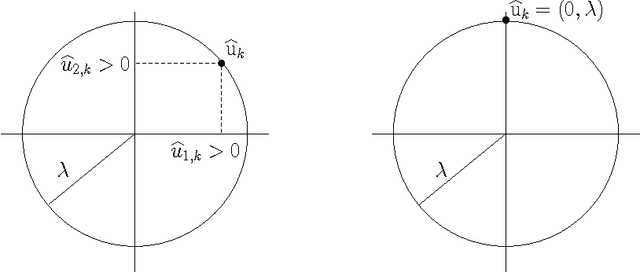
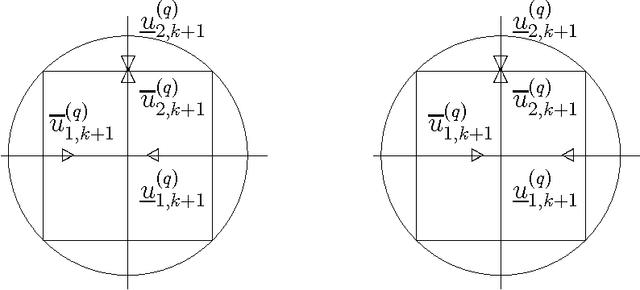
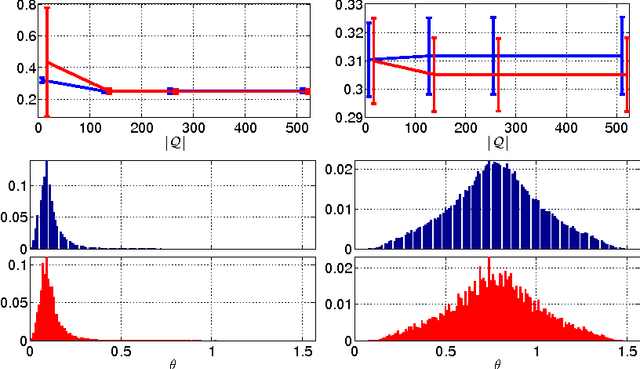
Abstract:In the context of change-point detection, addressed by Total Variation minimization strategies, an efficient on-the-fly algorithm has been designed leading to exact solutions for univariate data. In this contribution, an extension of such an on-the-fly strategy to multivariate data is investigated. The proposed algorithm relies on the local validation of the Karush-Kuhn-Tucker conditions on the dual problem. Showing that the non-local nature of the multivariate setting precludes to obtain an exact on-the-fly solution, we devise an on-the-fly algorithm delivering an approximate solution, whose quality is controlled by a practitioner-tunable parameter, acting as a trade-off between quality and computational cost. Performance assessment shows that high quality solutions are obtained on-the-fly while benefiting of computational costs several orders of magnitude lower than standard iterative procedures. The proposed algorithm thus provides practitioners with an efficient multivariate change-point detection on-the-fly procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge