Equivariant plug-and-play image reconstruction

Plug-and-play algorithms constitute a popular framework for solving inverse imaging problems that rely on the implicit definition of an image prior via a denoiser. These algorithms can leverage powerful pre-trained denoisers to solve a wide range of imaging tasks, circumventing the necessity to train models on a per-task basis. Unfortunately, plug-and-play methods often show unstable behaviors, hampering their promise of versatility and leading to suboptimal quality of reconstructed images. In this work, we show that enforcing equivariance to certain groups of transformations (rotations, reflections, and/or translations) on the denoiser strongly improves the stability of the algorithm as well as its reconstruction quality. We provide a theoretical analysis that illustrates the role of equivariance on better performance and stability. We present a simple algorithm that enforces equivariance on any existing denoiser by simply applying a random transformation to the input of the denoiser and the inverse transformation to the output at each iteration of the algorithm. Experiments on multiple imaging modalities and denoising networks show that the equivariant plug-and-play algorithm improves both the reconstruction performance and the stability compared to their non-equivariant counterparts.

PNN: From proximal algorithms to robust unfolded image denoising networks and Plug-and-Play methods

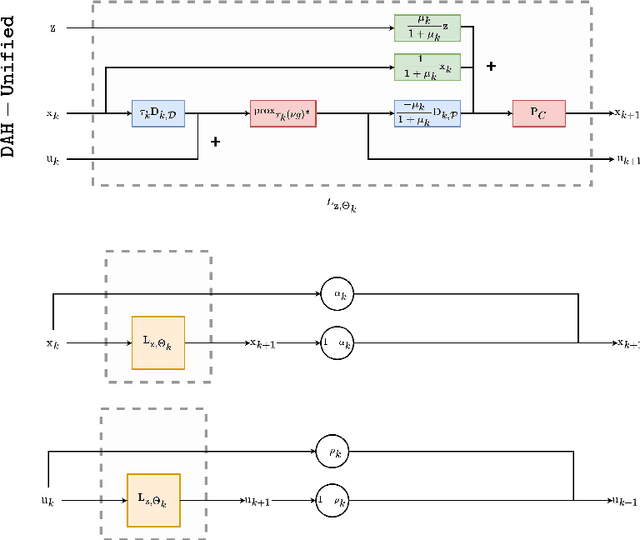
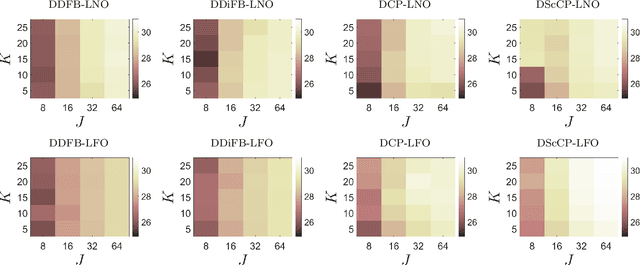
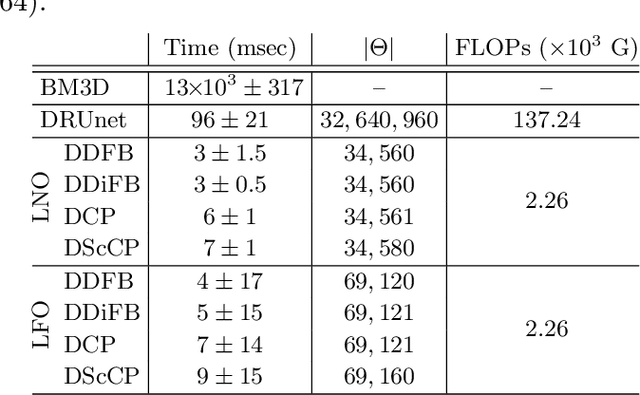
A common approach to solve inverse imaging problems relies on finding a maximum a posteriori (MAP) estimate of the original unknown image, by solving a minimization problem. In thiscontext, iterative proximal algorithms are widely used, enabling to handle non-smooth functions and linear operators. Recently, these algorithms have been paired with deep learning strategies, to further improve the estimate quality. In particular, proximal neural networks (PNNs) have been introduced, obtained by unrolling a proximal algorithm as for finding a MAP estimate, but over a fixed number of iterations, with learned linear operators and parameters. As PNNs are based on optimization theory, they are very flexible, and can be adapted to any image restoration task, as soon as a proximal algorithm can solve it. They further have much lighter architectures than traditional networks. In this article we propose a unified framework to build PNNs for the Gaussian denoising task, based on both the dual-FB and the primal-dual Chambolle-Pock algorithms. We further show that accelerated inertial versions of these algorithms enable skip connections in the associated NN layers. We propose different learning strategies for our PNN framework, and investigate their robustness (Lipschitz property) and denoising efficiency. Finally, we assess the robustness of our PNNs when plugged in a forward-backward algorithm for an image deblurring problem.

Covid19 Reproduction Number: Credibility Intervals by Blockwise Proximal Monte Carlo Samplers

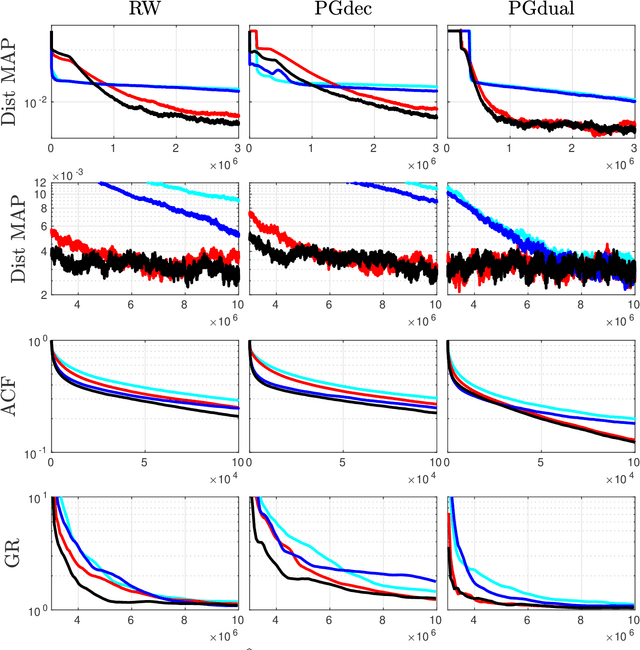
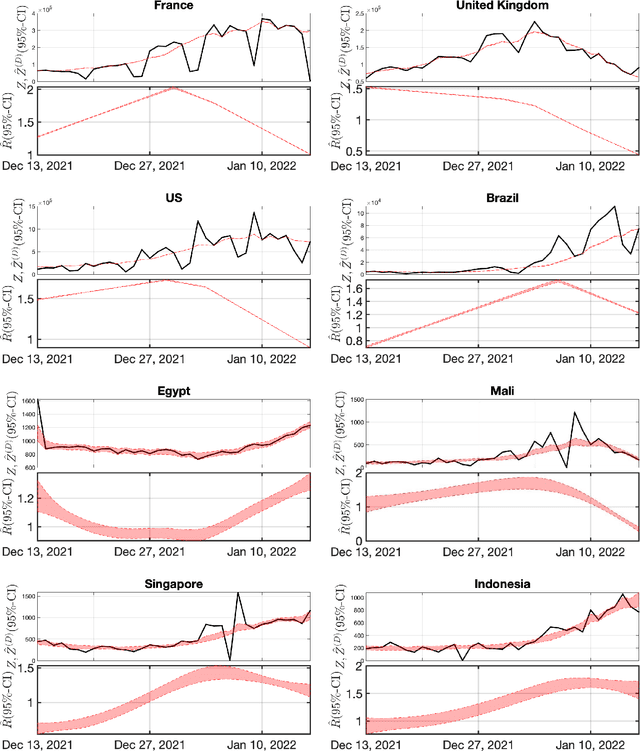
Monitoring the Covid19 pandemic constitutes a critical societal stake that received considerable research efforts. The intensity of the pandemic on a given territory is efficiently measured by the reproduction number, quantifying the rate of growth of daily new infections. Recently, estimates for the time evolution of the reproduction number were produced using an inverse problem formulation with a nonsmooth functional minimization. While it was designed to be robust to the limited quality of the Covid19 data (outliers, missing counts), the procedure lacks the ability to output credibility interval based estimates. This remains a severe limitation for practical use in actual pandemic monitoring by epidemiologists that the present work aims to overcome by use of Monte Carlo sampling. After interpretation of the functional into a Bayesian framework, several sampling schemes are tailored to adjust the nonsmooth nature of the resulting posterior distribution. The originality of the devised algorithms stems from combining a Langevin Monte Carlo sampling scheme with Proximal operators. Performance of the new algorithms in producing relevant credibility intervals for the reproduction number estimates and denoised counts are compared. Assessment is conducted on real daily new infection counts made available by the Johns Hopkins University. The interest of the devised monitoring tools are illustrated on Covid19 data from several different countries.

Alternative design of DeepPDNet in the context of image restoration

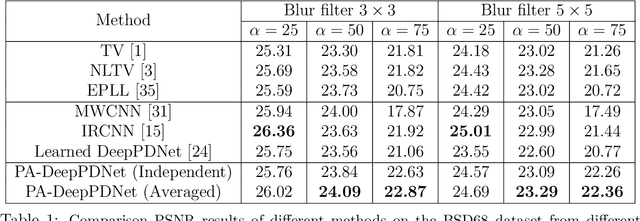
This work designs an image restoration deep network relying on unfolded Chambolle-Pock primal-dual iterations. Each layer of our network is built from Chambolle-Pock iterations when specified for minimizing a sum of a $\ell_2$-norm data-term and an analysis sparse prior. The parameters of our network are the step-sizes of the Chambolle-Pock scheme and the linear operator involved in sparsity-based penalization, including implicitly the regularization parameter. A backpropagation procedure is fully described. Preliminary experiments illustrate the good behavior of such a deep primal-dual network in the context of image restoration on BSD68 database.

Hyperparameter selection for the Discrete Mumford-Shah functional

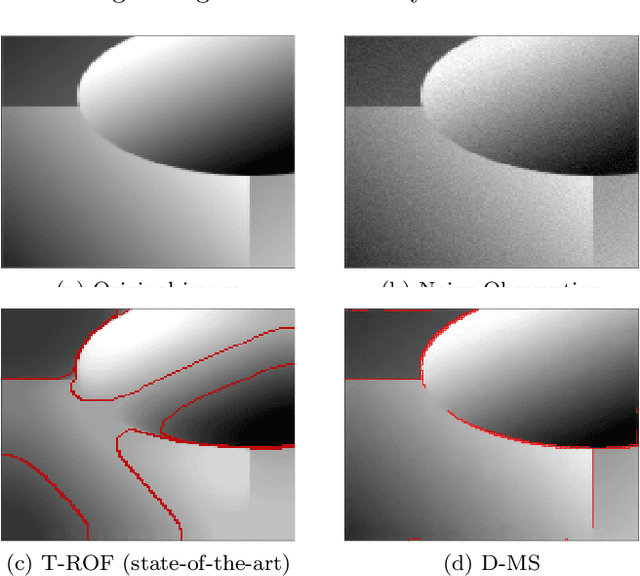
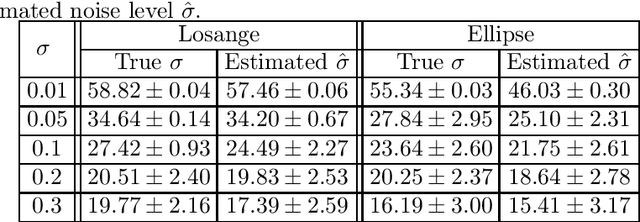
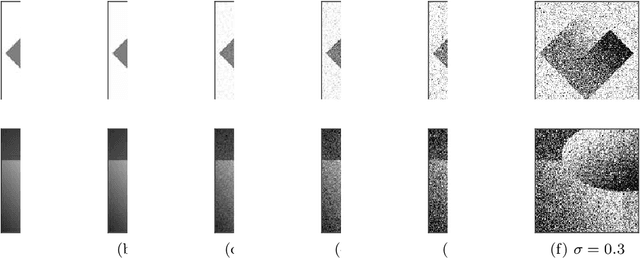
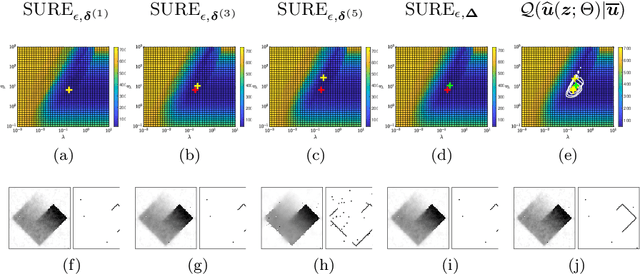
This work focuses on joint piecewise smooth image reconstruction and contour detection, formulated as the minimization of a discrete Mumford-Shah functional, performed via a theoretically grounded alternating minimization scheme. The bottleneck of such variational approaches lies in the need to finetune their hyperparameters, while not having access to ground truth data. To that aim, a Stein-like strategy providing optimal hyperparameters is designed, based on the minimization of an unbiased estimate of the quadratic risk. Efficient and automated minimization of the estimate of the risk crucially relies on an unbiased estimate of the gradient of the risk with respect to hyperparameters, whose practical implementation is performed thanks to a forward differentiation of the alternating scheme minimizing the Mumford-Shah functional, requiring exact differentiation of the proximity operators involved. Intensive numerical experiments are performed on synthetic images with different geometries and noise levels, assessing the accuracy and the robustness of the proposed procedure. The resulting parameterfree piecewise-smooth reconstruction and contour detection procedure, not requiring prior image processing expertise, is thus amenable to real-world applications.

Nonsmooth convex optimization to estimate the Covid-19 reproduction number space-time evolution with robustness against low quality data

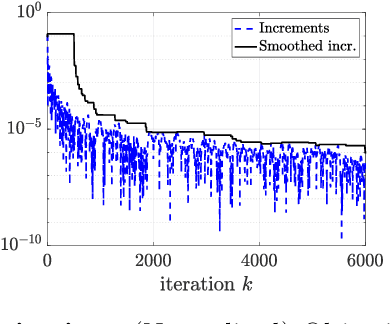
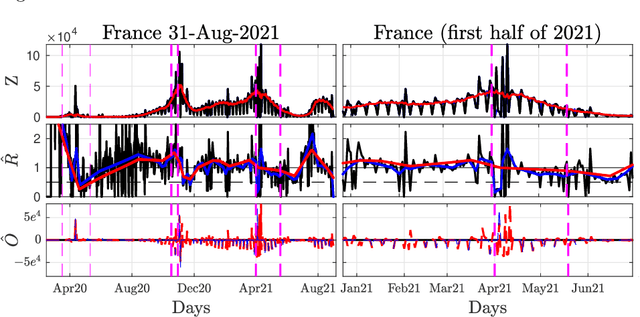
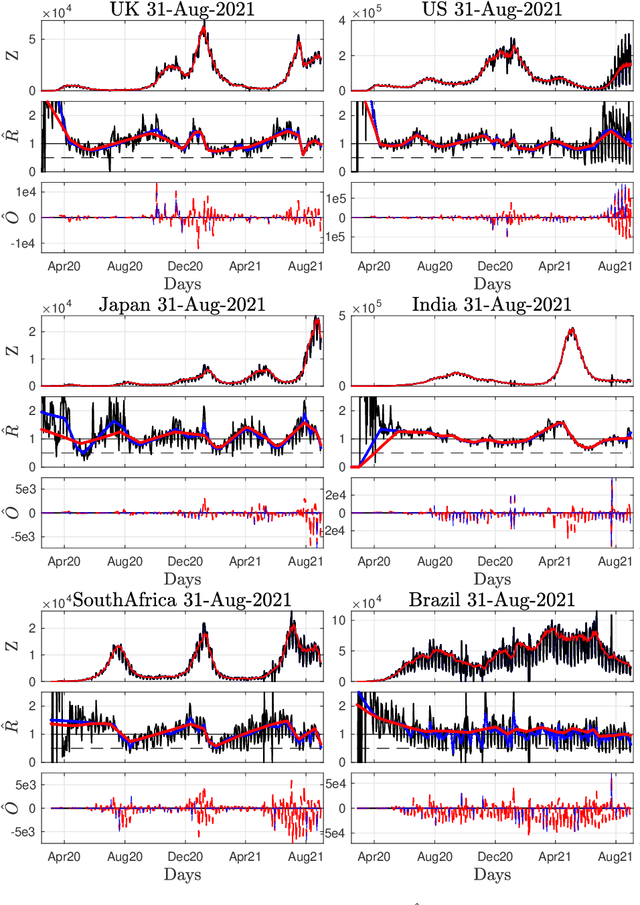
Daily pandemic surveillance, often achieved through the estimation of the reproduction number, constitutes a critical challenge for national health authorities to design countermeasures. In an earlier work, we proposed to formulate the estimation of the reproduction number as an optimization problem, combining data-model fidelity and space-time regularity constraints, solved by nonsmooth convex proximal minimizations. Though promising, that first formulation significantly lacks robustness against the Covid-19 data low quality (irrelevant or missing counts, pseudo-seasonalities,.. .) stemming from the emergency and crisis context, which significantly impairs accurate pandemic evolution assessments. The present work aims to overcome these limitations by carefully crafting a functional permitting to estimate jointly, in a single step, the reproduction number and outliers defined to model low quality data. This functional also enforces epidemiology-driven regularity properties for the reproduction number estimates, while preserving convexity, thus permitting the design of efficient minimization algorithms, based on proximity operators that are derived analytically. The explicit convergence of the proposed algorithm is proven theoretically. Its relevance is quantified on real Covid-19 data, consisting of daily new infection counts for 200+ countries and for the 96 metropolitan France counties, publicly available at Johns Hopkins University and Sant{\'e}-Publique-France. The procedure permits automated daily updates of these estimates, reported via animated and interactive maps. Open-source estimation procedures will be made publicly available.

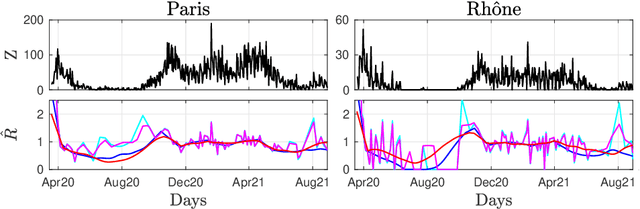
A deep primal-dual proximal network for image restoration

Image restoration remains a challenging task in image processing. Numerous methods have been proposed to tackle this problem, which is often solved by minimizing a non-smooth penalized likelihood function. Although the solution is easily interpretable with theoretic guarantees, its estimation relies on an optimization process. Considering the important research efforts in deep learning for image classification, they offers an alternative to perform image restoration but its adaptation to inverse problem is still challenging. In this work, we design a deep network, named DeepPDNet, built from primal-dual proximal iterations associated with the minimization of a standard penalized likelihood with an analysis prior, allowing us to take advantages from both worlds. We reformulate a specific instance of the Condat-Vu primal-dual hybrid gradient (PDHG) algorithm as a deep network with fixed layers. Each layer corresponds to one iteration of the primal-dual algorithm. The learned parameters are the primal-dual proximal algorithm step-size and the analysis linear operator involved in the penalization. These parameters are allowed to vary from a layer to another one. Two different learning strategies: "Full learning" and "Partial learning" are proposed, the first one is the most efficient numerically while the second one relies on standard constraints insuring convergence in the standard PDHG iterations. Moreover, global and local sparse analysis prior are studied to seek the better feature representation. We experiment the proposed DeepPDNet on the MNIST and BSD68 datasets with different blur and additive Gaussian noise. Extensive results shows that the proposed deep primal-dual proximal networks demonstrate excellent performance on the MNIST dataset compared to other state-of-the-art methods and better or at least comparable performance on the more complex BSD68 dataset.

Automated data-driven selection of the hyperparameters for Total-Variation based texture segmentation

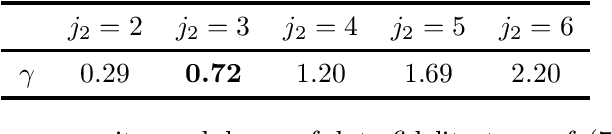
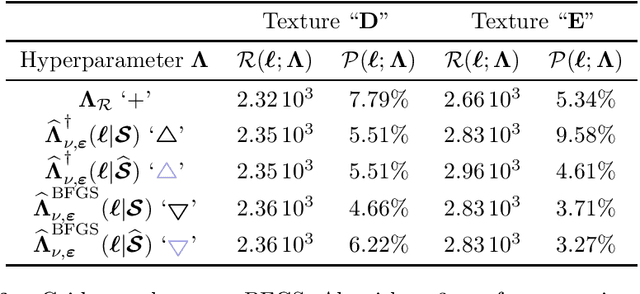
Penalized Least Squares are widely used in signal and image processing. Yet, it suffers from a major limitation since it requires fine-tuning of the regularization parameters. Under assumptions on the noise probability distribution, Stein-based approaches provide unbiased estimator of the quadratic risk. The Generalized Stein Unbiased Risk Estimator is revisited to handle correlated Gaussian noise without requiring to invert the covariance matrix. Then, in order to avoid expansive grid search, it is necessary to design algorithmic scheme minimizing the quadratic risk with respect to regularization parameters. This work extends the Stein's Unbiased GrAdient estimator of the Risk of Deledalle et al. to the case of correlated Gaussian noise, deriving a general automatic tuning of regularization parameters. First, the theoretical asymptotic unbiasedness of the gradient estimator is demonstrated in the case of general correlated Gaussian noise. Then, the proposed parameter selection strategy is particularized to fractal texture segmentation, where problem formulation naturally entails inter-scale and spatially correlated noise. Numerical assessment is provided, as well as discussion of the practical issues.

Solving NMF with smoothness and sparsity constraints using PALM

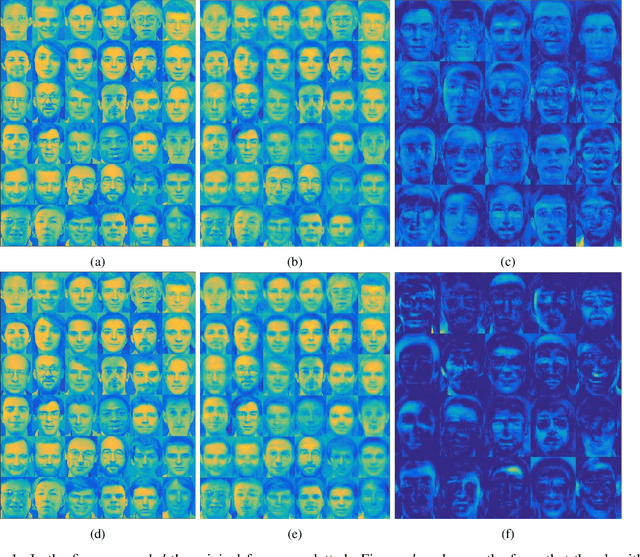
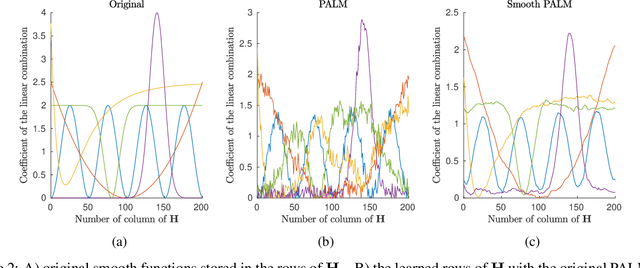
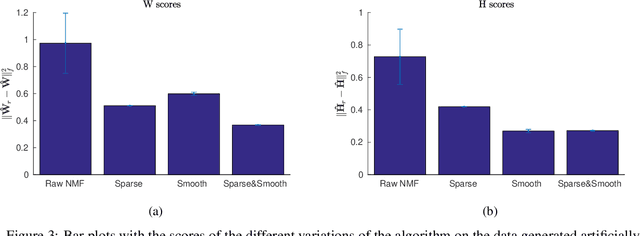
Non-negative matrix factorization is a problem of dimensionality reduction and source separation of data that has been widely used in many fields since it was studied in depth in 1999 by Lee and Seung, including in compression of data, document clustering, processing of audio spectrograms and astronomy. In this work we have adapted a minimization scheme for convex functions with non-differentiable constraints called PALM to solve the NMF problem with solutions that can be smooth and/or sparse, two properties frequently desired.

Sparse hierarchical interaction learning with epigraphical projection

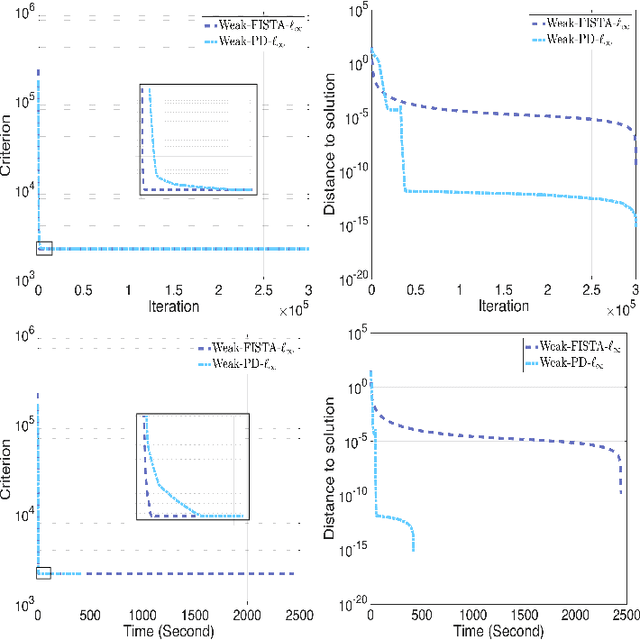
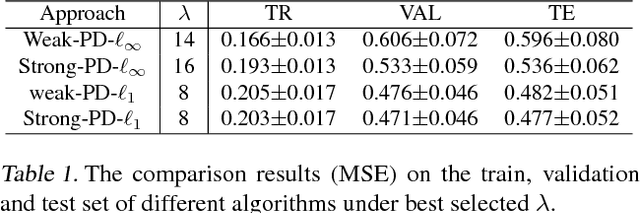
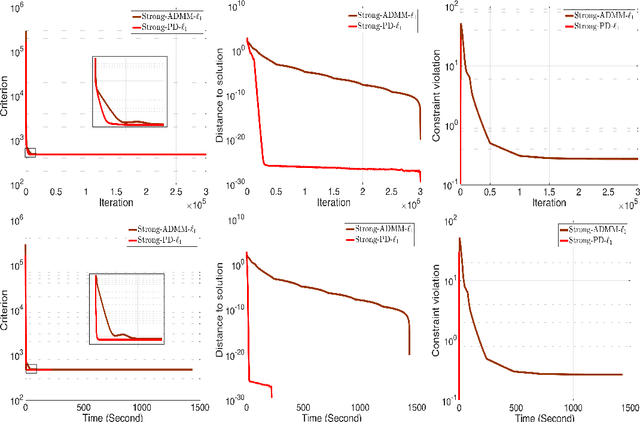
This work focus on regression optimization problem with hierarchical interactions between variables, which is beyond the additive models in the traditional linear regression. We investigate more specifically two different fashions encountered in the literature to deal with this problem: "hierNet" and structural-sparsity regularization, and study their connections. We propose a primal-dual proximal algorithm based on epigraphical projection to optimize a general formulation of this learning problem. The experimental setting first highlights the improvement of the proposed procedure compared to state-of-the-art methods based on fast iterative shrinkage-thresholding algorithm (i.e. FISTA) or alternating direction method of multipliers (i.e. ADMM) and second we provide fair comparisons between the different hierarchical penalizations. The experiments are conducted both on the synthetic and real data, and they clearly show that the proposed primal-dual proximal algorithm based on epigraphical projection is efficient and effective to solve and investigate the question of the hierarchical interaction learning problem.