Julian Tachella
Reconstruct Anything Model: a lightweight foundation model for computational imaging
Mar 11, 2025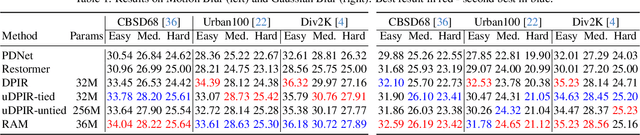
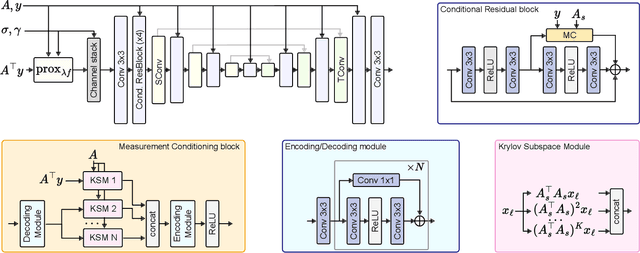
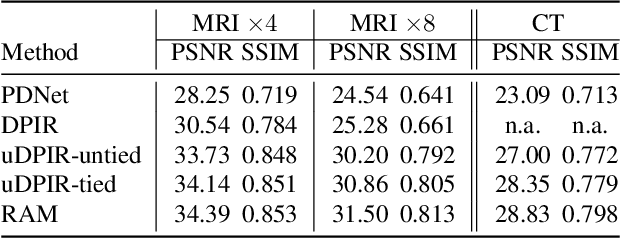
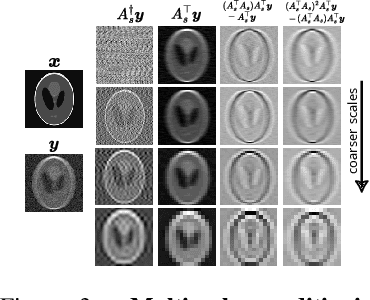
Abstract:Most existing learning-based methods for solving imaging inverse problems can be roughly divided into two classes: iterative algorithms, such as plug-and-play and diffusion methods, that leverage pretrained denoisers, and unrolled architectures that are trained end-to-end for specific imaging problems. Iterative methods in the first class are computationally costly and often provide suboptimal reconstruction performance, whereas unrolled architectures are generally specific to a single inverse problem and require expensive training. In this work, we propose a novel non-iterative, lightweight architecture that incorporates knowledge about the forward operator (acquisition physics and noise parameters) without relying on unrolling. Our model is trained to solve a wide range of inverse problems beyond denoising, including deblurring, magnetic resonance imaging, computed tomography, inpainting, and super-resolution. The proposed model can be easily adapted to unseen inverse problems or datasets with a few fine-tuning steps (up to a few images) in a self-supervised way, without ground-truth references. Throughout a series of experiments, we demonstrate state-of-the-art performance from medical imaging to low-photon imaging and microscopy.
Equivariant plug-and-play image reconstruction
Dec 04, 2023



Abstract:Plug-and-play algorithms constitute a popular framework for solving inverse imaging problems that rely on the implicit definition of an image prior via a denoiser. These algorithms can leverage powerful pre-trained denoisers to solve a wide range of imaging tasks, circumventing the necessity to train models on a per-task basis. Unfortunately, plug-and-play methods often show unstable behaviors, hampering their promise of versatility and leading to suboptimal quality of reconstructed images. In this work, we show that enforcing equivariance to certain groups of transformations (rotations, reflections, and/or translations) on the denoiser strongly improves the stability of the algorithm as well as its reconstruction quality. We provide a theoretical analysis that illustrates the role of equivariance on better performance and stability. We present a simple algorithm that enforces equivariance on any existing denoiser by simply applying a random transformation to the input of the denoiser and the inverse transformation to the output at each iteration of the algorithm. Experiments on multiple imaging modalities and denoising networks show that the equivariant plug-and-play algorithm improves both the reconstruction performance and the stability compared to their non-equivariant counterparts.
Equivariant Bootstrapping for Uncertainty Quantification in Imaging Inverse Problems
Oct 20, 2023Abstract:Scientific imaging problems are often severely ill-posed, and hence have significant intrinsic uncertainty. Accurately quantifying the uncertainty in the solutions to such problems is therefore critical for the rigorous interpretation of experimental results as well as for reliably using the reconstructed images as scientific evidence. Unfortunately, existing imaging methods are unable to quantify the uncertainty in the reconstructed images in a manner that is robust to experiment replications. This paper presents a new uncertainty quantification methodology based on an equivariant formulation of the parametric bootstrap algorithm that leverages symmetries and invariance properties commonly encountered in imaging problems. Additionally, the proposed methodology is general and can be easily applied with any image reconstruction technique, including unsupervised training strategies that can be trained from observed data alone, thus enabling uncertainty quantification in situations where there is no ground truth data available. We demonstrate the proposed approach with a series of numerical experiments and through comparisons with alternative uncertainty quantification strategies from the state-of-the-art, such as Bayesian strategies involving score-based diffusion models and Langevin samplers. In all our experiments, the proposed method delivers remarkably accurate high-dimensional confidence regions and outperforms the competing approaches in terms of estimation accuracy, uncertainty quantification accuracy, and computing time.
Spline Sketches: An Efficient Approach for Photon Counting Lidar
Oct 13, 2022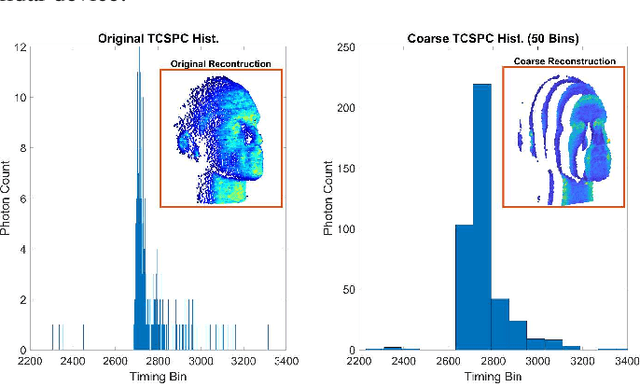

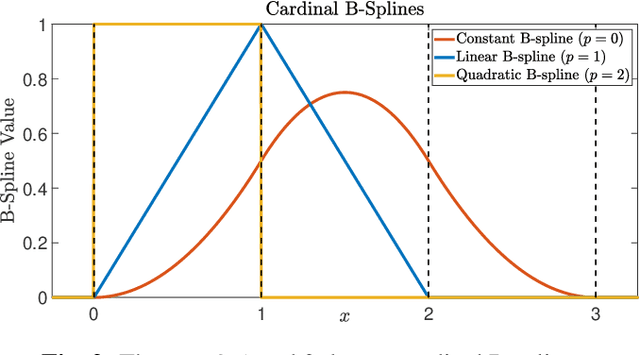

Abstract:Photon counting lidar has become an invaluable tool for 3D depth imaging due to the fine-precision it can achieve over long ranges. However, high frame rate, high resolution lidar devices produce an enormous amount of time-of-flight (ToF) data which can cause a severe data processing bottleneck hindering the deployment of real-time systems. In this paper, an efficient photon counting approach is proposed that exploits the simplicity of piecewise polynomial splines to form a hardware-friendly compressed statistic, or a so-called spline sketch, of the ToF data without sacrificing the quality of the recovered image. As each piecewise polynomial spline is a simple function with limited support over the timing depth window, the spline sketch can be computed efficiently on-chip with minimal computational overhead. \MD{We show that a piecewise linear or quadratic spline sketch, requiring minimal on-chip arithmetic computation per photon detection, can reconstruct real-world depth images with negligible loss of resolution whilst achieving $95\%$ compression compared to the full ToF data, as well as offering multi-peak detection performance. These contrast with previously proposed coarse binning histograms that suffer from a highly nonuniform accuracy across depth and can fail catastrophically when associated with bright reflectors. Further, by building range-walk correction into the proposed estimation algorithms, it is demonstrated that the spline sketches can be made robust to photon pile-up effects.} The computational complexity of both the reconstruction and range walk correction algorithms scale only with the size of the spline sketch which is independent to both the photon count and temporal resolution of the lidar device.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge