Matthieu Terris
MIND
DeepInverse: A Python package for solving imaging inverse problems with deep learning
May 26, 2025Abstract:DeepInverse is an open-source PyTorch-based library for solving imaging inverse problems. The library covers all crucial steps in image reconstruction from the efficient implementation of forward operators (e.g., optics, MRI, tomography), to the definition and resolution of variational problems and the design and training of advanced neural network architectures. In this paper, we describe the main functionality of the library and discuss the main design choices.
From Denoising Score Matching to Langevin Sampling: A Fine-Grained Error Analysis in the Gaussian Setting
Mar 14, 2025Abstract:Sampling from an unknown distribution, accessible only through discrete samples, is a fundamental problem at the core of generative AI. The current state-of-the-art methods follow a two-step process: first estimating the score function (the gradient of a smoothed log-distribution) and then applying a gradient-based sampling algorithm. The resulting distribution's correctness can be impacted by several factors: the generalization error due to a finite number of initial samples, the error in score matching, and the diffusion error introduced by the sampling algorithm. In this paper, we analyze the sampling process in a simple yet representative setting-sampling from Gaussian distributions using a Langevin diffusion sampler. We provide a sharp analysis of the Wasserstein sampling error that arises from the multiple sources of error throughout the pipeline. This allows us to rigorously track how the anisotropy of the data distribution (encoded by its power spectrum) interacts with key parameters of the end-to-end sampling method, including the noise amplitude, the step sizes in both score matching and diffusion, and the number of initial samples. Notably, we show that the Wasserstein sampling error can be expressed as a kernel-type norm of the data power spectrum, where the specific kernel depends on the method parameters. This result provides a foundation for further analysis of the tradeoffs involved in optimizing sampling accuracy, such as adapting the noise amplitude to the choice of step sizes.
Reconstruct Anything Model: a lightweight foundation model for computational imaging
Mar 11, 2025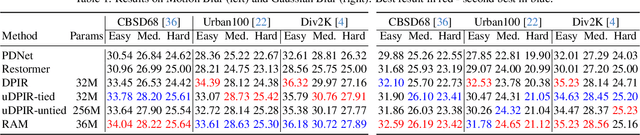
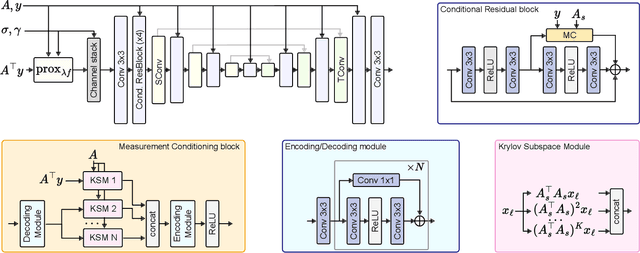
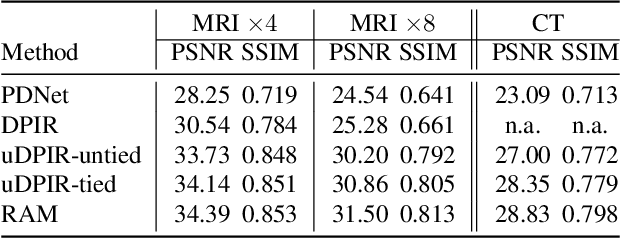
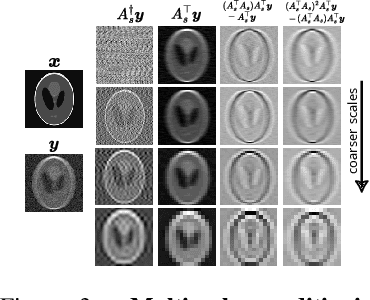
Abstract:Most existing learning-based methods for solving imaging inverse problems can be roughly divided into two classes: iterative algorithms, such as plug-and-play and diffusion methods, that leverage pretrained denoisers, and unrolled architectures that are trained end-to-end for specific imaging problems. Iterative methods in the first class are computationally costly and often provide suboptimal reconstruction performance, whereas unrolled architectures are generally specific to a single inverse problem and require expensive training. In this work, we propose a novel non-iterative, lightweight architecture that incorporates knowledge about the forward operator (acquisition physics and noise parameters) without relying on unrolling. Our model is trained to solve a wide range of inverse problems beyond denoising, including deblurring, magnetic resonance imaging, computed tomography, inpainting, and super-resolution. The proposed model can be easily adapted to unseen inverse problems or datasets with a few fine-tuning steps (up to a few images) in a self-supervised way, without ground-truth references. Throughout a series of experiments, we demonstrate state-of-the-art performance from medical imaging to low-photon imaging and microscopy.
FiRe: Fixed-points of Restoration Priors for Solving Inverse Problems
Nov 28, 2024Abstract:Selecting an appropriate prior to compensate for information loss due to the measurement operator is a fundamental challenge in imaging inverse problems. Implicit priors based on denoising neural networks have become central to widely-used frameworks such as Plug-and-Play (PnP) algorithms. In this work, we introduce Fixed-points of Restoration (FiRe) priors as a new framework for expanding the notion of priors in PnP to general restoration models beyond traditional denoising models. The key insight behind FiRe is that natural images emerge as fixed points of the composition of a degradation operator with the corresponding restoration model. This enables us to derive an explicit formula for our implicit prior by quantifying invariance of images under this composite operation. Adopting this fixed-point perspective, we show how various restoration networks can effectively serve as priors for solving inverse problems. The FiRe framework further enables ensemble-like combinations of multiple restoration models as well as acquisition-informed restoration networks, all within a unified optimization approach. Experimental results validate the effectiveness of FiRe across various inverse problems, establishing a new paradigm for incorporating pretrained restoration models into PnP-like algorithms.
Robust plug-and-play methods for highly accelerated non-Cartesian MRI reconstruction
Nov 04, 2024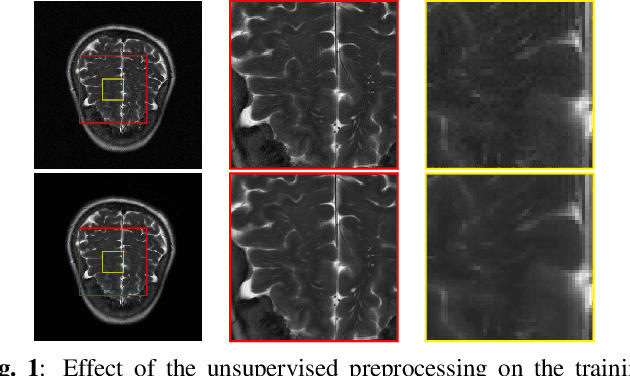
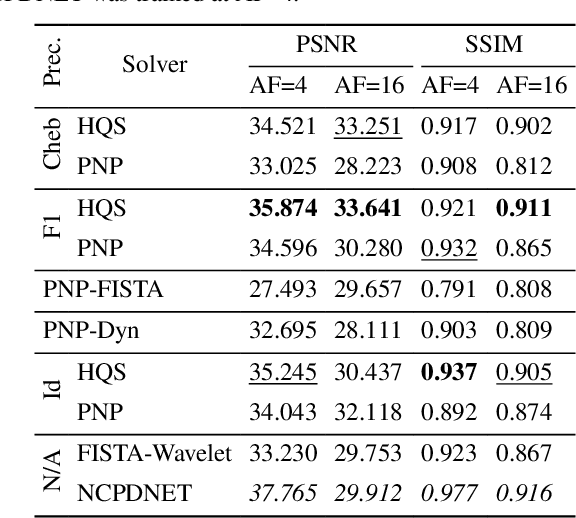
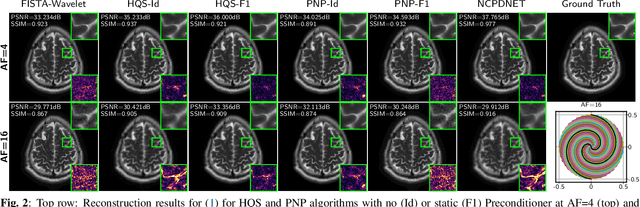
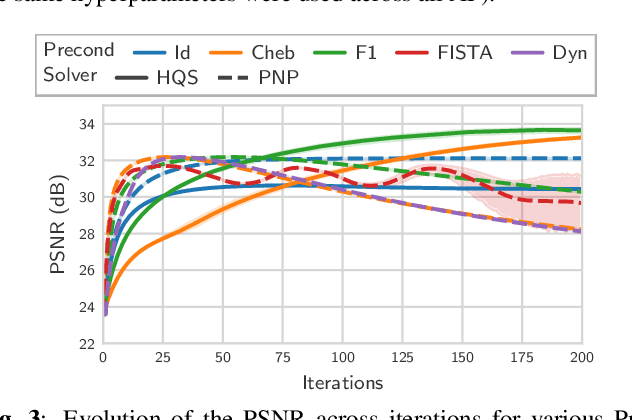
Abstract:Achieving high-quality Magnetic Resonance Imaging (MRI) reconstruction at accelerated acquisition rates remains challenging due to the inherent ill-posed nature of the inverse problem. Traditional Compressed Sensing (CS) methods, while robust across varying acquisition settings, struggle to maintain good reconstruction quality at high acceleration factors ($\ge$ 8). Recent advances in deep learning have improved reconstruction quality, but purely data-driven methods are prone to overfitting and hallucination effects, notably when the acquisition setting is varying. Plug-and-Play (PnP) approaches have been proposed to mitigate the pitfalls of both frameworks. In a nutshell, PnP algorithms amount to replacing suboptimal handcrafted CS priors with powerful denoising deep neural network (DNNs). However, in MRI reconstruction, existing PnP methods often yield suboptimal results due to instabilities in the proximal gradient descent (PGD) schemes and the lack of curated, noiseless datasets for training robust denoisers. In this work, we propose a fully unsupervised preprocessing pipeline to generate clean, noiseless complex MRI signals from multicoil data, enabling training of a high-performance denoising DNN. Furthermore, we introduce an annealed Half-Quadratic Splitting (HQS) algorithm to address the instability issues, leading to significant improvements over existing PnP algorithms. When combined with preconditioning techniques, our approach achieves state-of-the-art results, providing a robust and efficient solution for high-quality MRI reconstruction.
Plug-and-play imaging with model uncertainty quantification in radio astronomy
Dec 14, 2023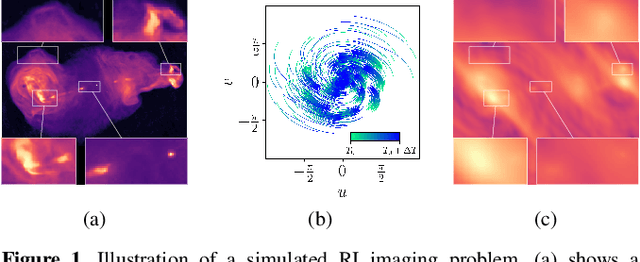

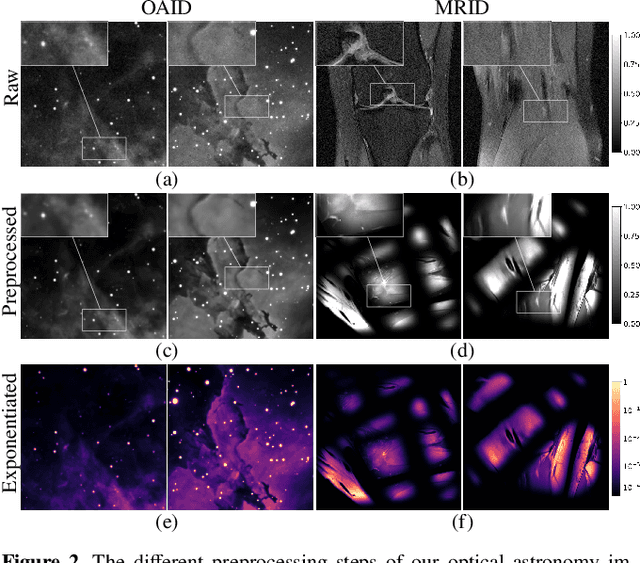
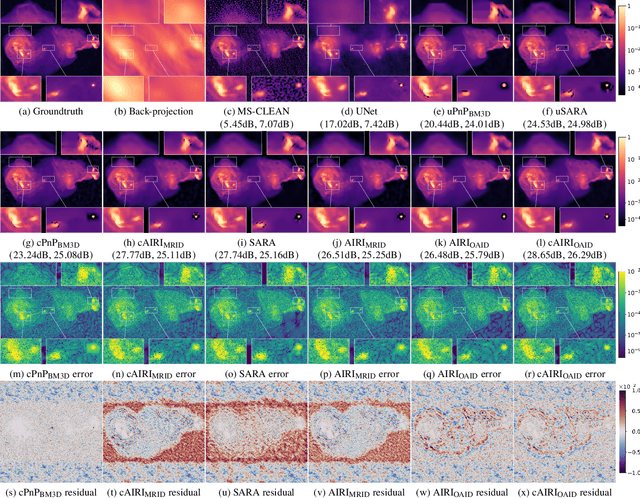
Abstract:Plug-and-Play (PnP) algorithms are appealing alternatives to proximal algorithms when solving inverse imaging problems. By learning a Deep Neural Network (DNN) behaving as a proximal operator, one waives the computational complexity of optimisation algorithms induced by sophisticated image priors, and the sub-optimality of handcrafted priors compared to DNNs. At the same time, these methods inherit the versatility of optimisation algorithms allowing the minimisation of a large class of objective functions. Such features are highly desirable in radio-interferometric (RI) imaging in astronomy, where the data size, the ill-posedness of the problem and the dynamic range of the target reconstruction are critical. In a previous work, we introduced a class of convergent PnP algorithms, dubbed AIRI, relying on a forward-backward algorithm, with a differentiable data-fidelity term and dynamic range-specific denoisers trained on highly pre-processed unrelated optical astronomy images. Here, we show that AIRI algorithms can benefit from a constrained data fidelity term at the mere cost of transferring to a primal-dual forward-backward algorithmic backbone. Moreover, we show that AIRI algorithms are robust to strong variations in the nature of the training dataset: denoisers trained on MRI images yield similar reconstructions to those trained on astronomical data. We additionally quantify the model uncertainty introduced by the randomness in the training process and suggest that AIRI algorithms are robust to model uncertainty. Finally, we propose an exhaustive comparison with methods from the radio-astronomical imaging literature and show the superiority of the proposed method over the current state-of-the-art.
Equivariant plug-and-play image reconstruction
Dec 04, 2023



Abstract:Plug-and-play algorithms constitute a popular framework for solving inverse imaging problems that rely on the implicit definition of an image prior via a denoiser. These algorithms can leverage powerful pre-trained denoisers to solve a wide range of imaging tasks, circumventing the necessity to train models on a per-task basis. Unfortunately, plug-and-play methods often show unstable behaviors, hampering their promise of versatility and leading to suboptimal quality of reconstructed images. In this work, we show that enforcing equivariance to certain groups of transformations (rotations, reflections, and/or translations) on the denoiser strongly improves the stability of the algorithm as well as its reconstruction quality. We provide a theoretical analysis that illustrates the role of equivariance on better performance and stability. We present a simple algorithm that enforces equivariance on any existing denoiser by simply applying a random transformation to the input of the denoiser and the inverse transformation to the output at each iteration of the algorithm. Experiments on multiple imaging modalities and denoising networks show that the equivariant plug-and-play algorithm improves both the reconstruction performance and the stability compared to their non-equivariant counterparts.
Meta-Prior: Meta learning for Adaptive Inverse Problem Solvers
Nov 30, 2023


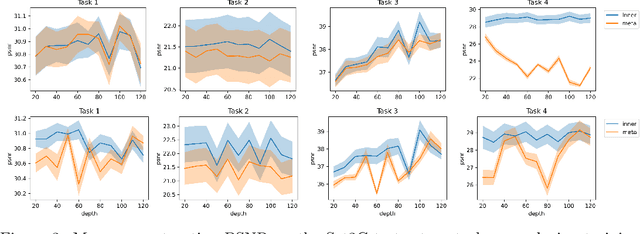
Abstract:Deep neural networks have become a foundational tool for addressing imaging inverse problems. They are typically trained for a specific task, with a supervised loss to learn a mapping from the observations to the image to recover. However, real-world imaging challenges often lack ground truth data, rendering traditional supervised approaches ineffective. Moreover, for each new imaging task, a new model needs to be trained from scratch, wasting time and resources. To overcome these limitations, we introduce a novel approach based on meta-learning. Our method trains a meta-model on a diverse set of imaging tasks that allows the model to be efficiently fine-tuned for specific tasks with few fine-tuning steps. We show that the proposed method extends to the unsupervised setting, where no ground truth data is available. In its bilevel formulation, the outer level uses a supervised loss, that evaluates how well the fine-tuned model performs, while the inner loss can be either supervised or unsupervised, relying only on the measurement operator. This allows the meta-model to leverage a few ground truth samples for each task while being able to generalize to new imaging tasks. We show that in simple settings, this approach recovers the Bayes optimal estimator, illustrating the soundness of our approach. We also demonstrate our method's effectiveness on various tasks, including image processing and magnetic resonance imaging.
Deep network series for large-scale high-dynamic range imaging
Oct 28, 2022



Abstract:We propose a new approach for large-scale high-dynamic range computational imaging. Deep Neural Networks (DNNs) trained end-to-end can solve linear inverse imaging problems almost instantaneously. While unfolded architectures provide necessary robustness to variations of the measurement setting, embedding large-scale measurement operators in DNN architectures is impractical. Alternative Plug-and-Play (PnP) approaches, where the denoising DNNs are blind to the measurement setting, have proven effective to address scalability and high-dynamic range challenges, but rely on highly iterative algorithms. We propose a residual DNN series approach, where the reconstructed image is built as a sum of residual images progressively increasing the dynamic range, and estimated iteratively by DNNs taking the back-projected data residual of the previous iteration as input. We demonstrate on simulations for radio-astronomical imaging that a series of only few terms provides a high-dynamic range reconstruction of similar quality to state-of-the-art PnP approaches, at a fraction of the cost.
Image reconstruction algorithms in radio interferometry: from handcrafted to learned denoisers
Feb 25, 2022
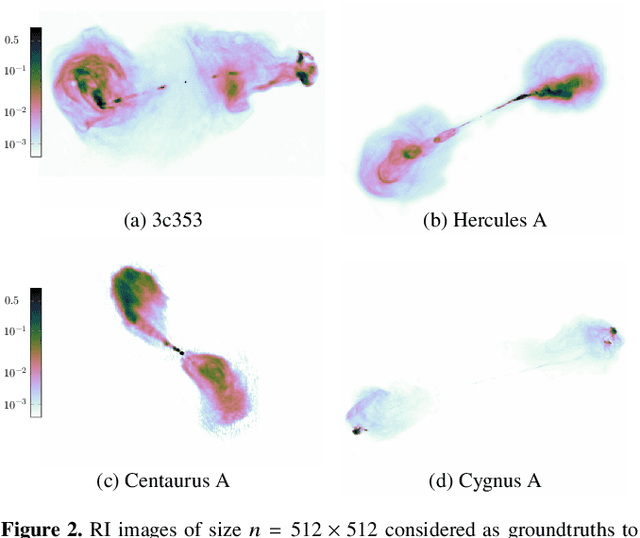
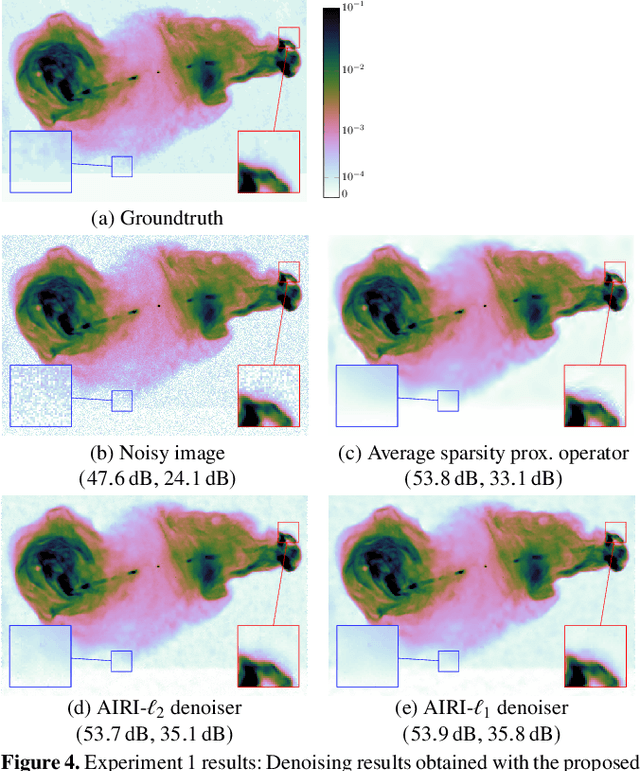
Abstract:We introduce a new class of iterative image reconstruction algorithms for radio interferometry, at the interface of convex optimization and deep learning, inspired by plug-and-play methods. The approach consists in learning a prior image model by training a deep neural network (DNN) as a denoiser, and substituting it for the handcrafted proximal regularization operator of an optimization algorithm. The proposed AIRI ("AI for Regularization in Radio-Interferometric Imaging") framework, for imaging complex intensity structure with diffuse and faint emission, inherits the robustness and interpretability of optimization, and the learning power and speed of networks. Our approach relies on three steps. Firstly, we design a low dynamic range database for supervised training from optical intensity images. Secondly, we train a DNN denoiser with basic architecture ensuring positivity of the output image, at a noise level inferred from the signal-to-noise ratio of the data. We use either $\ell_2$ or $\ell_1$ training losses, enhanced with a nonexpansiveness term ensuring algorithm convergence, and including on-the-fly database dynamic range enhancement via exponentiation. Thirdly, we plug the learned denoiser into the forward-backward optimization algorithm, resulting in a simple iterative structure alternating a denoising step with a gradient-descent data-fidelity step. The resulting AIRI-$\ell_2$ and AIRI-$\ell_1$ were validated against CLEAN and optimization algorithms of the SARA family, propelled by the "average sparsity" proximal regularization operator. Simulation results show that these first AIRI incarnations are competitive in imaging quality with SARA and its unconstrained forward-backward-based version uSARA, while providing significant acceleration. CLEAN remains faster but offers lower reconstruction quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge