Yves Wiaux
MROP: Modulated Rank-One Projections for compressive radio interferometric imaging
Apr 25, 2025Abstract:The emerging generation of radio-interferometric (RI) arrays are set to form images of the sky with a new regime of sensitivity and resolution. This implies a significant increase in visibility data volumes, scaling as $\mathcal{O}(Q^{2}B)$ for $Q$ antennas and $B$ short-time integration intervals (or batches), calling for efficient data dimensionality reduction techniques. This paper proposes a new approach to data compression during acquisition, coined modulated rank-one projection (MROP). MROP compresses the $Q\times Q$ batchwise covariance matrix into a smaller number $P$ of random rank-one projections and compresses across time by trading $B$ for a smaller number $M$ of random modulations of the ROP measurement vectors. Firstly, we introduce a dual perspective on the MROP acquisition, which can either be understood as random beamforming, or as a post-correlation compression. Secondly, we analyse the noise statistics of MROPs and demonstrate that the random projections induce a uniform noise level across measurements independently of the visibility-weighting scheme used. Thirdly, we propose a detailed analysis of the memory and computational cost requirements across the data acquisition and image reconstruction stages, with comparison to state-of-the-art dimensionality reduction approaches. Finally, the MROP model is validated in simulation for monochromatic intensity imaging, with comparison to the classical and baseline-dependent averaging (BDA) models, and using the uSARA optimisation algorithm for image formation. An extensive experimental setup is considered, with ground-truth images containing diffuse and faint emission and spanning a wide variety of dynamic ranges, and for a range of $uv$-coverages corresponding to VLA and MeerKAT observation.
The R2D2 Deep Neural Network Series for Scalable Non-Cartesian Magnetic Resonance Imaging
Mar 13, 2025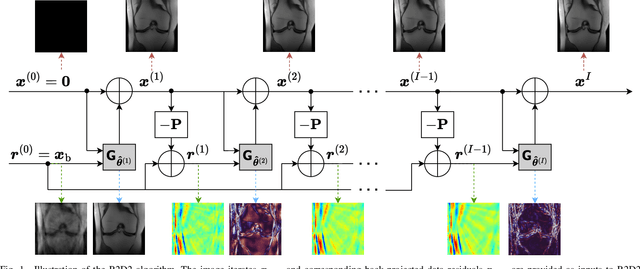
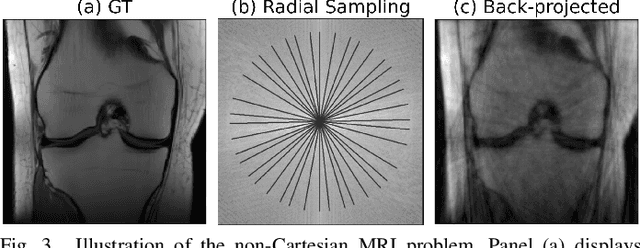
Abstract:We introduce the R2D2 Deep Neural Network (DNN) series paradigm for fast and scalable image reconstruction from highly-accelerated non-Cartesian k-space acquisitions in Magnetic Resonance Imaging (MRI). While unrolled DNN architectures provide a robust image formation approach via data-consistency layers, embedding non-uniform fast Fourier transform operators in a DNN can become impractical to train at large scale, e.g in 2D MRI with a large number of coils, or for higher-dimensional imaging. Plug-and-play approaches that alternate a learned denoiser blind to the measurement setting with a data-consistency step are not affected by this limitation but their highly iterative nature implies slow reconstruction. To address this scalability challenge, we leverage the R2D2 paradigm that was recently introduced to enable ultra-fast reconstruction for large-scale Fourier imaging in radio astronomy. R2D2's reconstruction is formed as a series of residual images iteratively estimated as outputs of DNN modules taking the previous iteration's data residual as input. The method can be interpreted as a learned version of the Matching Pursuit algorithm. A series of R2D2 DNN modules were sequentially trained in a supervised manner on the fastMRI dataset and validated for 2D multi-coil MRI in simulation and on real data, targeting highly under-sampled radial k-space sampling. Results suggest that a series with only few DNNs achieves superior reconstruction quality over its unrolled incarnation R2D2-Net (whose training is also much less scalable), and over the state-of-the-art diffusion-based "Decomposed Diffusion Sampler" approach (also characterised by a slower reconstruction process).
Towards a robust R2D2 paradigm for radio-interferometric imaging: revisiting DNN training and architecture
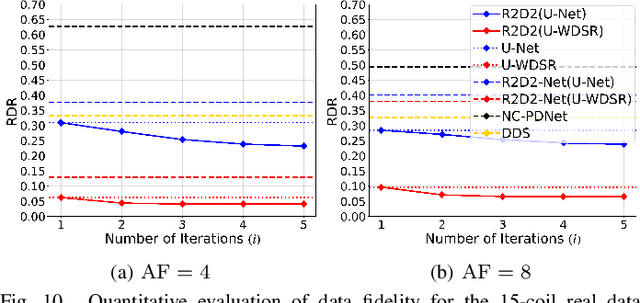
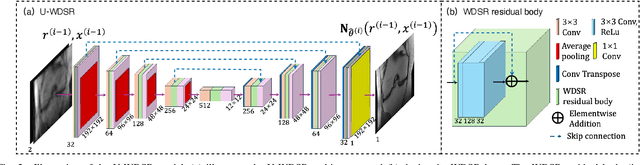
Mar 04, 2025Abstract:The R2D2 Deep Neural Network (DNN) series was recently introduced for image formation in radio interferometry. It can be understood as a learned version of CLEAN, whose minor cycles are substituted with DNNs. We revisit R2D2 on the grounds of series convergence, training methodology, and DNN architecture, improving its robustness in terms of generalisability beyond training conditions, capability to deliver high data fidelity, and epistemic uncertainty. Firstly, while still focusing on telescope-specific training, we enhance the learning process by randomising Fourier sampling integration times, incorporating multi-scan multi-noise configurations, and varying imaging settings, including pixel resolution and visibility-weighting scheme. Secondly, we introduce a convergence criterion whereby the reconstruction process stops when the data residual is compatible with noise, rather than simply using all available DNNs. This not only increases the reconstruction efficiency by reducing its computational cost, but also refines training by pruning out the data/image pairs for which optimal data fidelity is reached before training the next DNN. Thirdly, we substitute R2D2's early U-Net DNN with a novel architecture (U-WDSR) combining U-Net and WDSR, which leverages wide activation, dense connections, weight normalisation, and low-rank convolution to improve feature reuse and reconstruction precision. As previously, R2D2 was trained for monochromatic intensity imaging with the Very Large Array (VLA) at fixed $512 \times 512$ image size. Simulations on a wide range of inverse problems and a case study on real data reveal that the new R2D2 model consistently outperforms its earlier version in image reconstruction quality, data fidelity, and epistemic uncertainty.
Scalable Non-Cartesian Magnetic Resonance Imaging with R2D2
Mar 27, 2024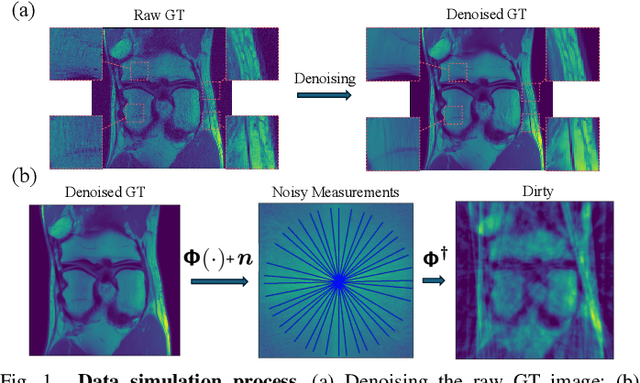
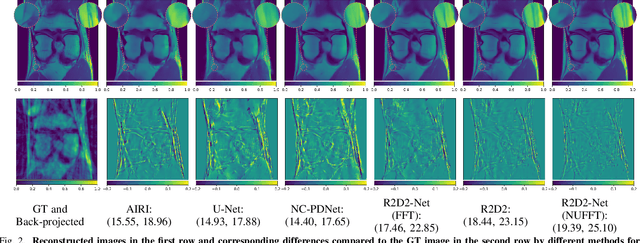
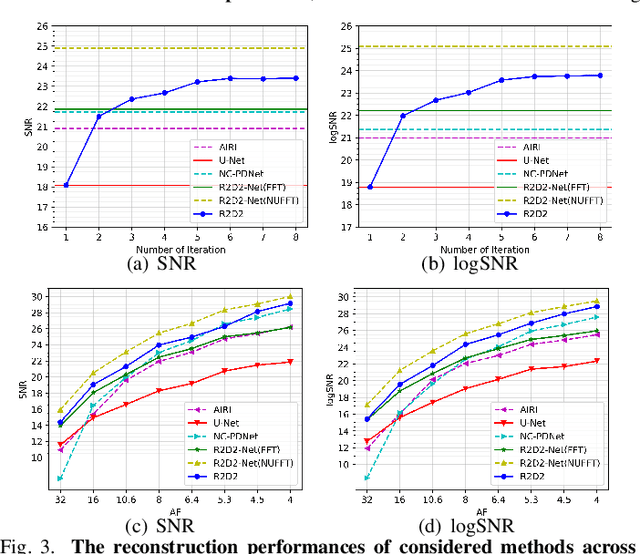
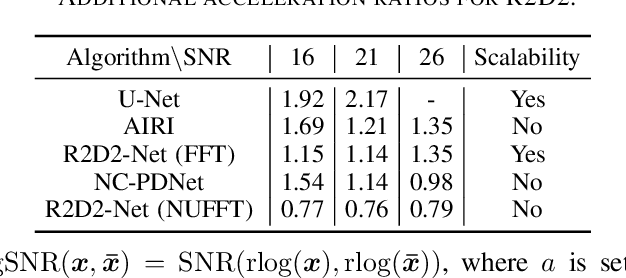
Abstract:We propose a new approach for non-Cartesian magnetic resonance image reconstruction. While unrolled architectures provide robustness via data-consistency layers, embedding measurement operators in Deep Neural Network (DNN) can become impractical at large scale. Alternative Plug-and-Play (PnP) approaches, where the denoising DNNs are blind to the measurement setting, are not affected by this limitation and have also proven effective, but their highly iterative nature also affects scalability. To address this scalability challenge, we leverage the "Residual-to-Residual DNN series for high-Dynamic range imaging (R2D2)" approach recently introduced in astronomical imaging. R2D2's reconstruction is formed as a series of residual images, iteratively estimated as outputs of DNNs taking the previous iteration's image estimate and associated data residual as inputs. The method can be interpreted as a learned version of the Matching Pursuit algorithm. We demonstrate R2D2 in simulation, considering radial k-space sampling acquisition sequences. Our preliminary results suggest that R2D2 achieves: (i) suboptimal performance compared to its unrolled incarnation R2D2-Net, which is however non-scalable due to the necessary embedding of NUFFT-based data-consistency layers; (ii) superior reconstruction quality to a scalable version of R2D2-Net embedding an FFT-based approximation for data consistency; (iii) superior reconstruction quality to PnP, while only requiring few iterations.
R2D2 image reconstruction with model uncertainty quantification in radio astronomy
Mar 26, 2024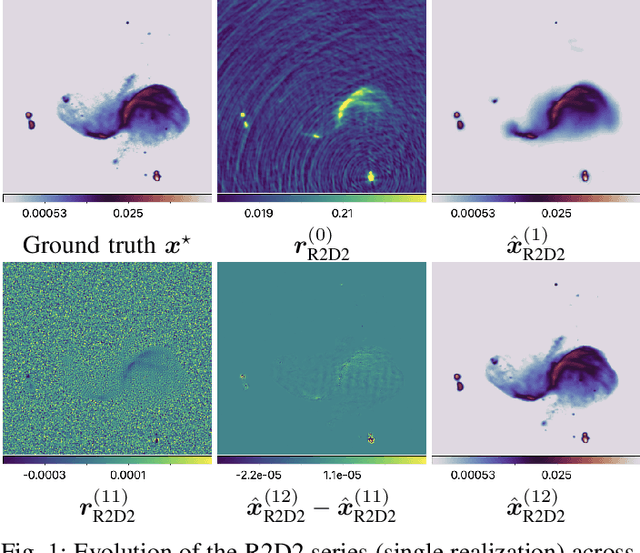
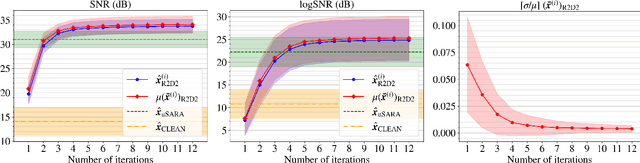
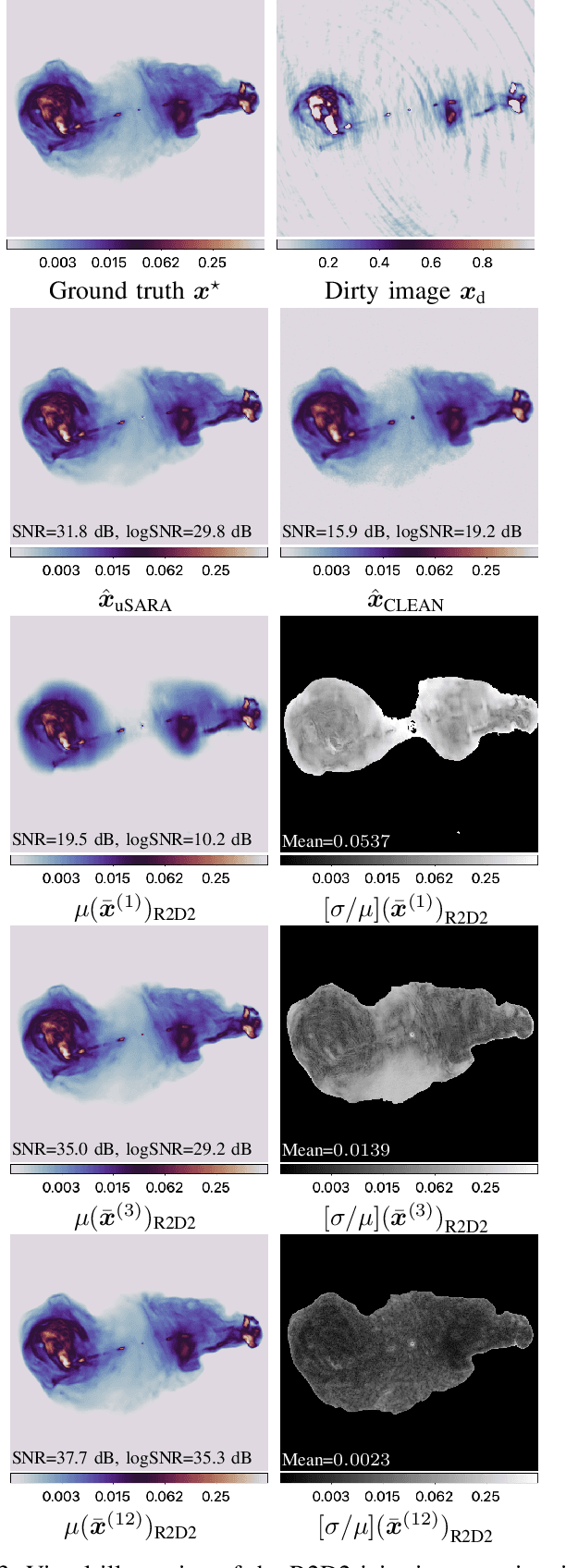

Abstract:The ``Residual-to-Residual DNN series for high-Dynamic range imaging'' (R2D2) approach was recently introduced for Radio-Interferometric (RI) imaging in astronomy. R2D2's reconstruction is formed as a series of residual images, iteratively estimated as outputs of Deep Neural Networks (DNNs) taking the previous iteration's image estimate and associated data residual as inputs. In this work, we investigate the robustness of the R2D2 image estimation process, by studying the uncertainty associated with its series of learned models. Adopting an ensemble averaging approach, multiple series can be trained, arising from different random DNN initializations of the training process at each iteration. The resulting multiple R2D2 instances can also be leveraged to generate ``R2D2 samples'', from which empirical mean and standard deviation endow the algorithm with a joint estimation and uncertainty quantification functionality. Focusing on RI imaging, and adopting a telescope-specific approach, multiple R2D2 instances were trained to encompass the most general observation setting of the Very Large Array (VLA). Simulations and real-data experiments confirm that: (i) R2D2's image estimation capability is superior to that of the state-of-the-art algorithms; (ii) its ultra-fast reconstruction capability (arising from series with only few DNNs) makes the computation of multiple reconstruction samples and of uncertainty maps practical even at large image dimension; (iii) it is characterized by a very low model uncertainty.
The R2D2 deep neural network series paradigm for fast precision imaging in radio astronomy
Mar 12, 2024Abstract:Radio-interferometric (RI) imaging entails solving high-resolution high-dynamic range inverse problems from large data volumes. Recent image reconstruction techniques grounded in optimization theory have demonstrated remarkable capability for imaging precision, well beyond CLEAN's capability. These range from advanced proximal algorithms propelled by handcrafted regularization operators, such as the SARA family, to hybrid plug-and-play (PnP) algorithms propelled by learned regularization denoisers, such as AIRI. Optimization and PnP structures are however highly iterative, which hinders their ability to handle the extreme data sizes expected from future instruments. To address this scalability challenge, we introduce a novel deep learning approach, dubbed ``Residual-to-Residual DNN series for high-Dynamic range imaging''. R2D2's reconstruction is formed as a series of residual images, iteratively estimated as outputs of Deep Neural Networks (DNNs) taking the previous iteration's image estimate and associated data residual as inputs. It thus takes a hybrid structure between a PnP algorithm and a learned version of the matching pursuit algorithm that underpins CLEAN. We present a comprehensive study of our approach, featuring its multiple incarnations distinguished by their DNN architectures. We provide a detailed description of its training process, targeting a telescope-specific approach. R2D2's capability to deliver high precision is demonstrated in simulation, across a variety of image and observation settings using the Very Large Array (VLA). Its reconstruction speed is also demonstrated: with only few iterations required to clean data residuals at dynamic ranges up to 100000, R2D2 opens the door to fast precision imaging. R2D2 codes are available in the BASPLib library on GitHub.
Plug-and-play imaging with model uncertainty quantification in radio astronomy
Dec 14, 2023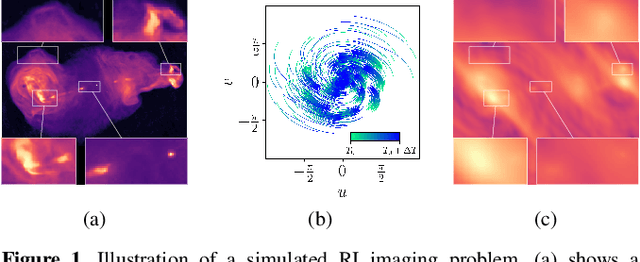

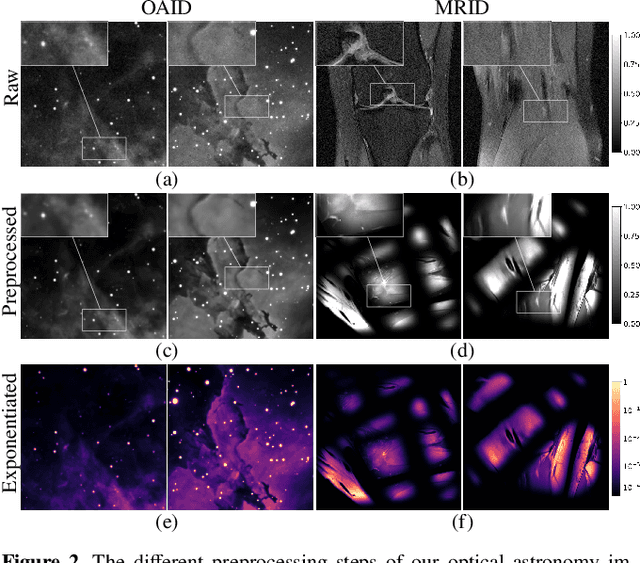
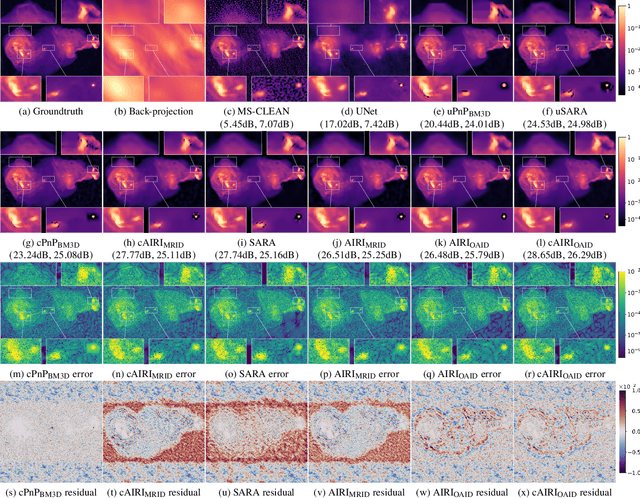
Abstract:Plug-and-Play (PnP) algorithms are appealing alternatives to proximal algorithms when solving inverse imaging problems. By learning a Deep Neural Network (DNN) behaving as a proximal operator, one waives the computational complexity of optimisation algorithms induced by sophisticated image priors, and the sub-optimality of handcrafted priors compared to DNNs. At the same time, these methods inherit the versatility of optimisation algorithms allowing the minimisation of a large class of objective functions. Such features are highly desirable in radio-interferometric (RI) imaging in astronomy, where the data size, the ill-posedness of the problem and the dynamic range of the target reconstruction are critical. In a previous work, we introduced a class of convergent PnP algorithms, dubbed AIRI, relying on a forward-backward algorithm, with a differentiable data-fidelity term and dynamic range-specific denoisers trained on highly pre-processed unrelated optical astronomy images. Here, we show that AIRI algorithms can benefit from a constrained data fidelity term at the mere cost of transferring to a primal-dual forward-backward algorithmic backbone. Moreover, we show that AIRI algorithms are robust to strong variations in the nature of the training dataset: denoisers trained on MRI images yield similar reconstructions to those trained on astronomical data. We additionally quantify the model uncertainty introduced by the randomness in the training process and suggest that AIRI algorithms are robust to model uncertainty. Finally, we propose an exhaustive comparison with methods from the radio-astronomical imaging literature and show the superiority of the proposed method over the current state-of-the-art.
Deep network series for large-scale high-dynamic range imaging
Oct 28, 2022



Abstract:We propose a new approach for large-scale high-dynamic range computational imaging. Deep Neural Networks (DNNs) trained end-to-end can solve linear inverse imaging problems almost instantaneously. While unfolded architectures provide necessary robustness to variations of the measurement setting, embedding large-scale measurement operators in DNN architectures is impractical. Alternative Plug-and-Play (PnP) approaches, where the denoising DNNs are blind to the measurement setting, have proven effective to address scalability and high-dynamic range challenges, but rely on highly iterative algorithms. We propose a residual DNN series approach, where the reconstructed image is built as a sum of residual images progressively increasing the dynamic range, and estimated iteratively by DNNs taking the back-projected data residual of the previous iteration as input. We demonstrate on simulations for radio-astronomical imaging that a series of only few terms provides a high-dynamic range reconstruction of similar quality to state-of-the-art PnP approaches, at a fraction of the cost.
Parallel faceted imaging in radio interferometry via proximal splitting (Faceted HyperSARA): II. Code and real data proof of concept
Sep 15, 2022
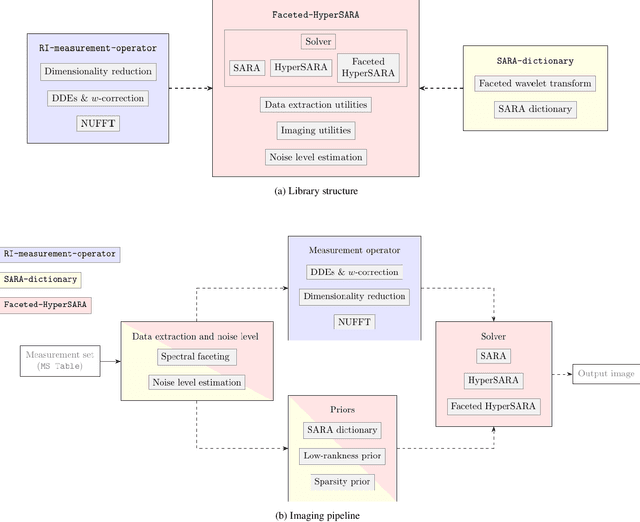
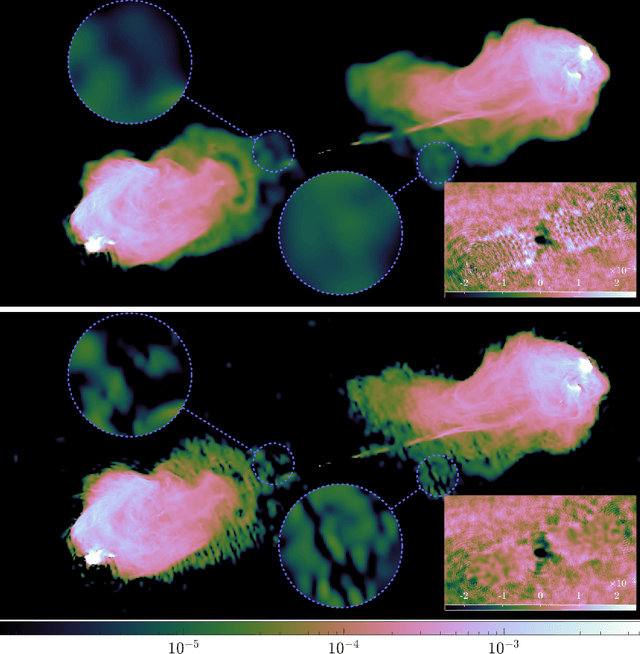
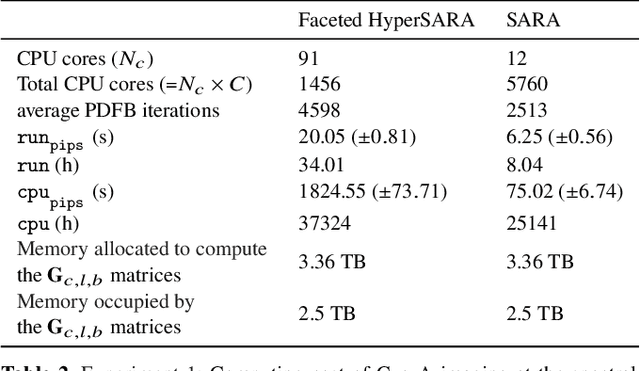
Abstract:In a companion paper, a faceted wideband imaging technique for radio interferometry, dubbed Faceted HyperSARA, has been introduced and validated on synthetic data. Building on the recent HyperSARA approach, Faceted HyperSARA leverages the splitting functionality inherent to the underlying primal-dual forward-backward algorithm to decompose the image reconstruction over multiple spatio-spectral facets. The approach allows complex regularization to be injected into the imaging process while providing additional parallelization flexibility compared to HyperSARA. The present paper introduces new algorithm functionalities to address real datasets, implemented as part of a fully fledged MATLAB imaging library made available on Github. A large scale proof-of-concept is proposed to validate Faceted HyperSARA in a new data and parameter scale regime, compared to the state-of-the-art. The reconstruction of a 15 GB wideband image of Cyg A from 7.4 GB of VLA data is considered, utilizing 1440 CPU cores on a HPC system for about 9 hours. The conducted experiments illustrate the reconstruction performance of the proposed approach on real data, exploiting new functionalities to set, both an accurate model of the measurement operator accounting for known direction-dependent effects (DDEs), and an effective noise level accounting for imperfect calibration. They also demonstrate that, when combined with a further dimensionality reduction functionality, Faceted HyperSARA enables the recovery of a 3.6 GB image of Cyg A from the same data using only 91 CPU cores for 39 hours. In this setting, the proposed approach is shown to provide a superior reconstruction quality compared to the state-of-the-art wideband CLEAN-based algorithm of the WSClean software.
Image reconstruction algorithms in radio interferometry: from handcrafted to learned denoisers
Feb 25, 2022
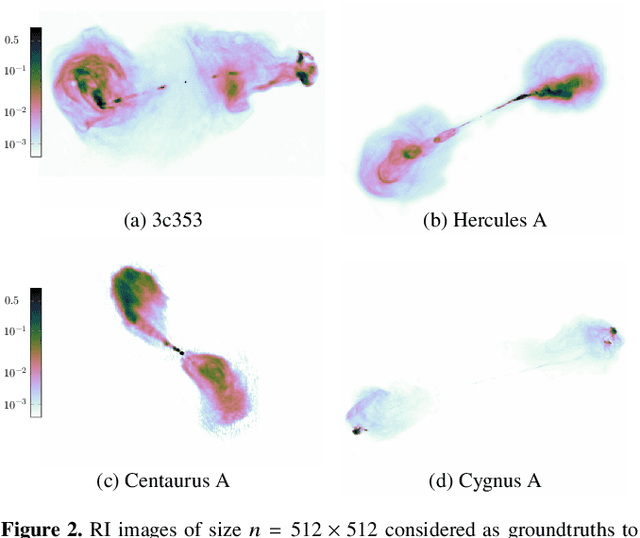
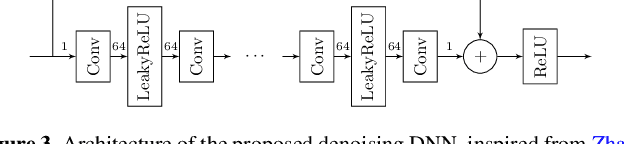
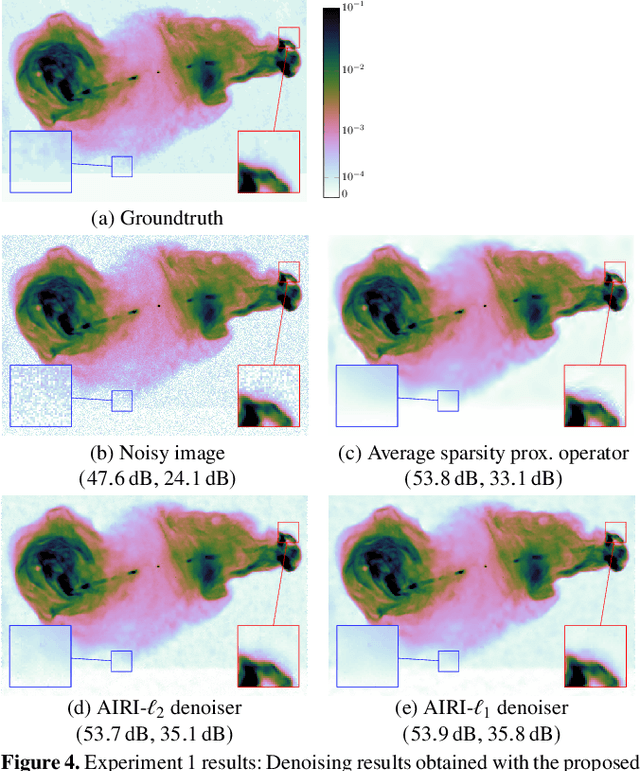
Abstract:We introduce a new class of iterative image reconstruction algorithms for radio interferometry, at the interface of convex optimization and deep learning, inspired by plug-and-play methods. The approach consists in learning a prior image model by training a deep neural network (DNN) as a denoiser, and substituting it for the handcrafted proximal regularization operator of an optimization algorithm. The proposed AIRI ("AI for Regularization in Radio-Interferometric Imaging") framework, for imaging complex intensity structure with diffuse and faint emission, inherits the robustness and interpretability of optimization, and the learning power and speed of networks. Our approach relies on three steps. Firstly, we design a low dynamic range database for supervised training from optical intensity images. Secondly, we train a DNN denoiser with basic architecture ensuring positivity of the output image, at a noise level inferred from the signal-to-noise ratio of the data. We use either $\ell_2$ or $\ell_1$ training losses, enhanced with a nonexpansiveness term ensuring algorithm convergence, and including on-the-fly database dynamic range enhancement via exponentiation. Thirdly, we plug the learned denoiser into the forward-backward optimization algorithm, resulting in a simple iterative structure alternating a denoising step with a gradient-descent data-fidelity step. The resulting AIRI-$\ell_2$ and AIRI-$\ell_1$ were validated against CLEAN and optimization algorithms of the SARA family, propelled by the "average sparsity" proximal regularization operator. Simulation results show that these first AIRI incarnations are competitive in imaging quality with SARA and its unconstrained forward-backward-based version uSARA, while providing significant acceleration. CLEAN remains faster but offers lower reconstruction quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge