A Hierarchical Likelihood Model for Non-linear Inverse Problems under Additive and Multiplicative Noise

Ill-posed inverse problems are encountered in numerous applications, possibly characterized by a highly non-linear forward model, both additive and multiplicative sources of noise, and censored data. In the absence of ground truth, uncertainty quantification is crucial to assess estimation reliability. This motivates the use of a Bayesian model and stochastic inference methods such as Markov Chain Monte Carlo algorithms. Problems combining all these challenges often lead to a complex and potentially multimodal posterior distribution, difficult to handle in practice. Approximate approaches have been proposed in the literature by either neglecting a source of noise or by using a tractable approximation of the likelihood function. These approaches either lead to an inaccurate model, or may require a complex calibration of the approximate likelihood. This paper proposes to tackle such problems with a general hierarchical Bayesian model and an efficient MCMC algorithm. The proposed formulation bypasses the need for calibrating the hyperparameters of an approximate model and is more versatile. The proposed method is assessed on a challenging scenario encountered in astronomy using synthetic data, in a variety of noise and censoring configurations. Comparisons are conducted against two baselines and a state-of-the-art method applicable in this context. The proposed approach is general and yields state-of-the-art results in terms of point-wise estimates and computing costs, with superior predictive performance. Results in the supplementary material further complete this comprehensive and rigorous model study. This work can serve as a guide for practitioners to select the best likelihood model according to their specific application.

Denoising bivariate signals via smoothing and polarization priors

We propose two formulations to leverage the geometric properties of bivariate signals for dealing with the denoising problem. In doing so, we use the instantaneous Stokes parameters to incorporate the polarization state of the signal. While the first formulation exploits the statistics of the Stokes representation in a Bayesian setting, the second uses a kernel regression formulation to impose locally smooth time-varying polarization properties. In turn, we obtain two formulations that allow us to use both signal and polarization domain regularization for denoising a bivariate signal. The solutions to them exploit the polarization information efficiently as demonstrated in the numerical simulations

A distributed Gibbs Sampler with Hypergraph Structure for High-Dimensional Inverse Problems

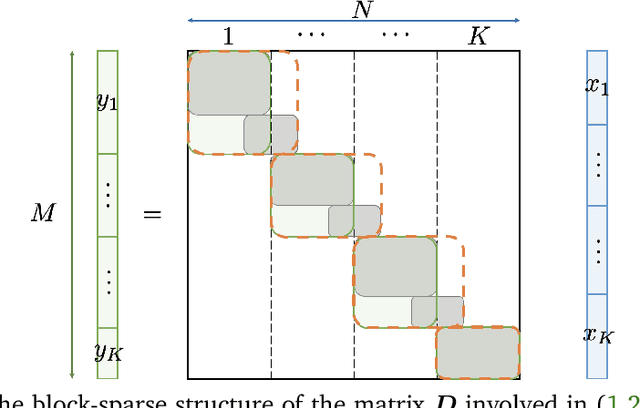
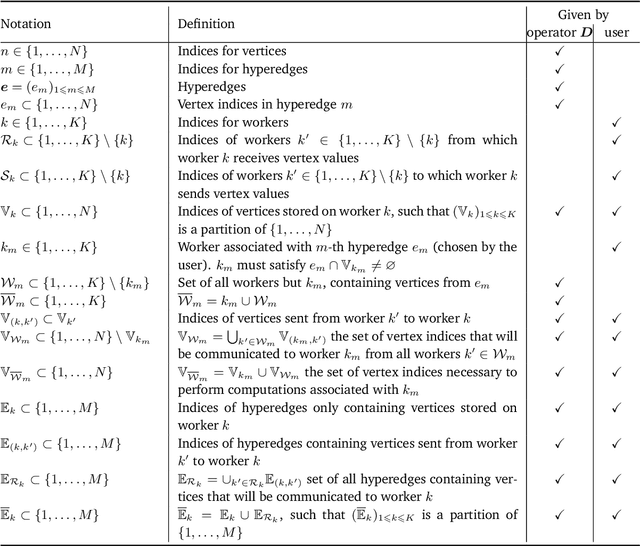
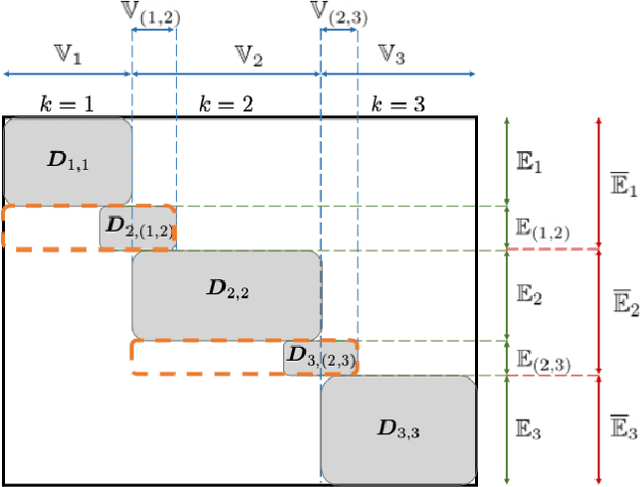
Sampling-based algorithms are classical approaches to perform Bayesian inference in inverse problems. They provide estimators with the associated credibility intervals to quantify the uncertainty on the estimators. Although these methods hardly scale to high dimensional problems, they have recently been paired with optimization techniques, such as proximal and splitting approaches, to address this issue. Such approaches pave the way to distributed samplers, splitting computations to make inference more scalable and faster. We introduce a distributed Gibbs sampler to efficiently solve such problems, considering posterior distributions with multiple smooth and non-smooth functions composed with linear operators. The proposed approach leverages a recent approximate augmentation technique reminiscent of primal-dual optimization methods. It is further combined with a block-coordinate approach to split the primal and dual variables into blocks, leading to a distributed block-coordinate Gibbs sampler. The resulting algorithm exploits the hypergraph structure of the involved linear operators to efficiently distribute the variables over multiple workers under controlled communication costs. It accommodates several distributed architectures, such as the Single Program Multiple Data and client-server architectures. Experiments on a large image deblurring problem show the performance of the proposed approach to produce high quality estimates with credibility intervals in a small amount of time.

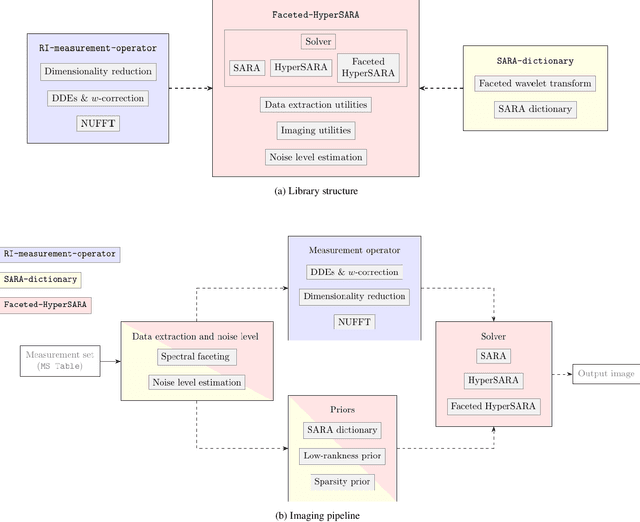
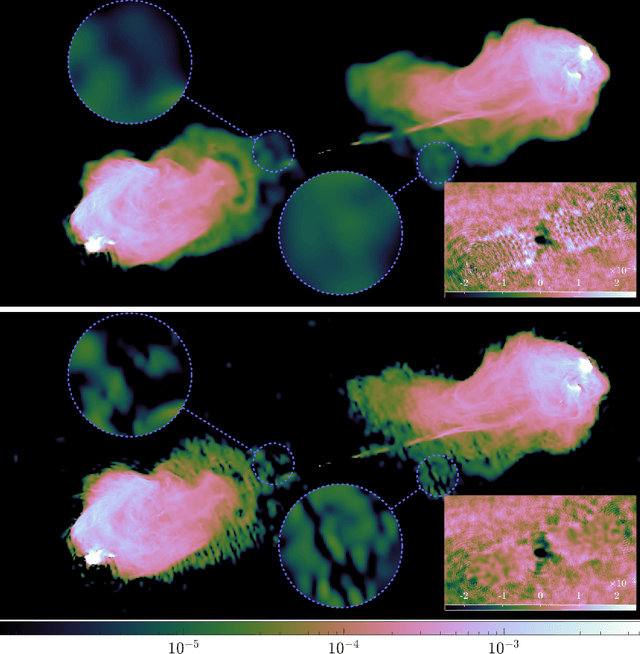
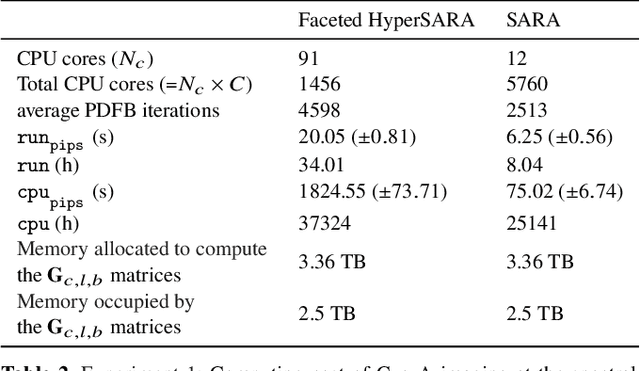
Parallel faceted imaging in radio interferometry via proximal splitting (Faceted HyperSARA): II. Code and real data proof of concept

In a companion paper, a faceted wideband imaging technique for radio interferometry, dubbed Faceted HyperSARA, has been introduced and validated on synthetic data. Building on the recent HyperSARA approach, Faceted HyperSARA leverages the splitting functionality inherent to the underlying primal-dual forward-backward algorithm to decompose the image reconstruction over multiple spatio-spectral facets. The approach allows complex regularization to be injected into the imaging process while providing additional parallelization flexibility compared to HyperSARA. The present paper introduces new algorithm functionalities to address real datasets, implemented as part of a fully fledged MATLAB imaging library made available on Github. A large scale proof-of-concept is proposed to validate Faceted HyperSARA in a new data and parameter scale regime, compared to the state-of-the-art. The reconstruction of a 15 GB wideband image of Cyg A from 7.4 GB of VLA data is considered, utilizing 1440 CPU cores on a HPC system for about 9 hours. The conducted experiments illustrate the reconstruction performance of the proposed approach on real data, exploiting new functionalities to set, both an accurate model of the measurement operator accounting for known direction-dependent effects (DDEs), and an effective noise level accounting for imperfect calibration. They also demonstrate that, when combined with a further dimensionality reduction functionality, Faceted HyperSARA enables the recovery of a 3.6 GB image of Cyg A from the same data using only 91 CPU cores for 39 hours. In this setting, the proposed approach is shown to provide a superior reconstruction quality compared to the state-of-the-art wideband CLEAN-based algorithm of the WSClean software.

Online Unmixing of Multitemporal Hyperspectral Images accounting for Spectral Variability

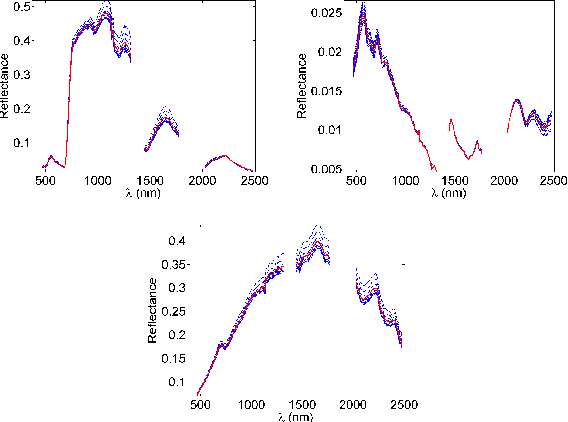
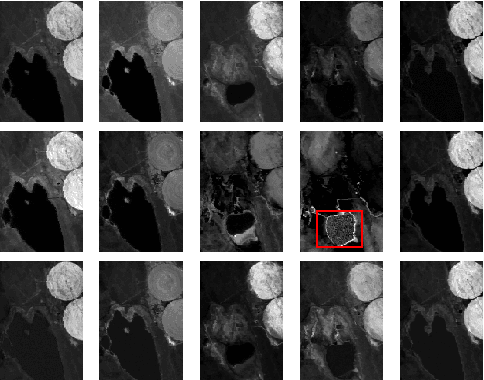
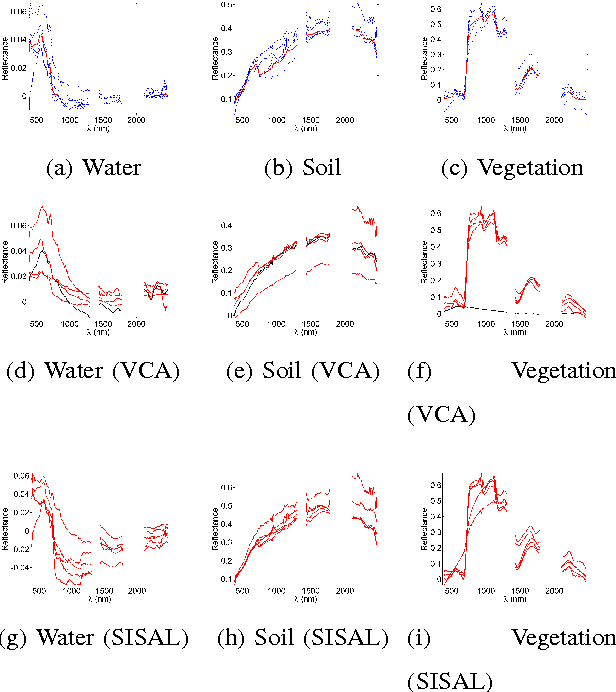
Hyperspectral unmixing is aimed at identifying the reference spectral signatures composing an hyperspectral image and their relative abundance fractions in each pixel. In practice, the identified signatures may vary spectrally from an image to another due to varying acquisition conditions, thus inducing possibly significant estimation errors. Against this background, hyperspectral unmixing of several images acquired over the same area is of considerable interest. Indeed, such an analysis enables the endmembers of the scene to be tracked and the corresponding endmember variability to be characterized. Sequential endmember estimation from a set of hyperspectral images is expected to provide improved performance when compared to methods analyzing the images independently. However, the significant size of hyperspectral data precludes the use of batch procedures to jointly estimate the mixture parameters of a sequence of hyperspectral images. Provided that each elementary component is present in at least one image of the sequence, we propose to perform an online hyperspectral unmixing accounting for temporal endmember variability. The online hyperspectral unmixing is formulated as a two-stage stochastic program, which can be solved using a stochastic approximation. The performance of the proposed method is evaluated on synthetic and real data. A comparison with independent unmixing algorithms finally illustrates the interest of the proposed strategy.