Analysis and Synthesis Denoisers for Forward-Backward Plug-and-Play Algorithms

In this work we study the behavior of the forward-backward (FB) algorithm when the proximity operator is replaced by a sub-iterative procedure to approximate a Gaussian denoiser, in a Plug-and-Play (PnP) fashion. In particular, we consider both analysis and synthesis Gaussian denoisers within a dictionary framework, obtained by unrolling dual-FB iterations or FB iterations, respectively. We analyze the associated minimization problems as well as the asymptotic behavior of the resulting FB-PnP iterations. In particular, we show that the synthesis Gaussian denoising problem can be viewed as a proximity operator. For each case, analysis and synthesis, we show that the FB-PnP algorithms solve the same problem whether we use only one or an infinite number of sub-iteration to solve the denoising problem at each iteration. To this aim, we show that each "one sub-iteration" strategy within the FB-PnP can be interpreted as a primal-dual algorithm when a warm-restart strategy is used. We further present similar results when using a Moreau-Yosida smoothing of the global problem, for an arbitrary number of sub-iterations. Finally, we provide numerical simulations to illustrate our theoretical results. In particular we first consider a toy compressive sensing example, as well as an image restoration problem in a deep dictionary framework.

A lifted Bregman strategy for training unfolded proximal neural network Gaussian denoisers

Unfolded proximal neural networks (PNNs) form a family of methods that combines deep learning and proximal optimization approaches. They consist in designing a neural network for a specific task by unrolling a proximal algorithm for a fixed number of iterations, where linearities can be learned from prior training procedure. PNNs have shown to be more robust than traditional deep learning approaches while reaching at least as good performances, in particular in computational imaging. However, training PNNs still depends on the efficiency of available training algorithms. In this work, we propose a lifted training formulation based on Bregman distances for unfolded PNNs. Leveraging the deterministic mini-batch block-coordinate forward-backward method, we design a bespoke computational strategy beyond traditional back-propagation methods for solving the resulting learning problem efficiently. We assess the behaviour of the proposed training approach for PNNs through numerical simulations on image denoising, considering a denoising PNN whose structure is based on dual proximal-gradient iterations.

Learning truly monotone operators with applications to nonlinear inverse problems

This article introduces a novel approach to learning monotone neural networks through a newly defined penalization loss. The proposed method is particularly effective in solving classes of variational problems, specifically monotone inclusion problems, commonly encountered in image processing tasks. The Forward-Backward-Forward (FBF) algorithm is employed to address these problems, offering a solution even when the Lipschitz constant of the neural network is unknown. Notably, the FBF algorithm provides convergence guarantees under the condition that the learned operator is monotone. Building on plug-and-play methodologies, our objective is to apply these newly learned operators to solving non-linear inverse problems. To achieve this, we initially formulate the problem as a variational inclusion problem. Subsequently, we train a monotone neural network to approximate an operator that may not inherently be monotone. Leveraging the FBF algorithm, we then show simulation examples where the non-linear inverse problem is successfully solved.

PNN: From proximal algorithms to robust unfolded image denoising networks and Plug-and-Play methods

A common approach to solve inverse imaging problems relies on finding a maximum a posteriori (MAP) estimate of the original unknown image, by solving a minimization problem. In thiscontext, iterative proximal algorithms are widely used, enabling to handle non-smooth functions and linear operators. Recently, these algorithms have been paired with deep learning strategies, to further improve the estimate quality. In particular, proximal neural networks (PNNs) have been introduced, obtained by unrolling a proximal algorithm as for finding a MAP estimate, but over a fixed number of iterations, with learned linear operators and parameters. As PNNs are based on optimization theory, they are very flexible, and can be adapted to any image restoration task, as soon as a proximal algorithm can solve it. They further have much lighter architectures than traditional networks. In this article we propose a unified framework to build PNNs for the Gaussian denoising task, based on both the dual-FB and the primal-dual Chambolle-Pock algorithms. We further show that accelerated inertial versions of these algorithms enable skip connections in the associated NN layers. We propose different learning strategies for our PNN framework, and investigate their robustness (Lipschitz property) and denoising efficiency. Finally, we assess the robustness of our PNNs when plugged in a forward-backward algorithm for an image deblurring problem.

A primal-dual data-driven method for computational optical imaging with a photonic lantern

Optical fibres aim to image in-vivo biological processes. In this context, high spatial resolution and stability to fibre movements are key to enable decision-making processes (e.g., for microendoscopy). Recently, a single-pixel imaging technique based on a multicore fibre photonic lantern has been designed, named computational optical imaging using a lantern (COIL). A proximal algorithm based on a sparsity prior, dubbed SARA-COIL, has been further proposed to enable image reconstructions for high resolution COIL microendoscopy. In this work, we develop a data-driven approach for COIL. We replace the sparsity prior in the proximal algorithm by a learned denoiser, leading to a plug-and-play (PnP) algorithm. We use recent results in learning theory to train a network with desirable Lipschitz properties. We show that the resulting primal-dual PnP algorithm converges to a solution to a monotone inclusion problem. Our simulations highlight that the proposed data-driven approach improves the reconstruction quality over variational SARA-COIL method on both simulated and real data.

A distributed Gibbs Sampler with Hypergraph Structure for High-Dimensional Inverse Problems

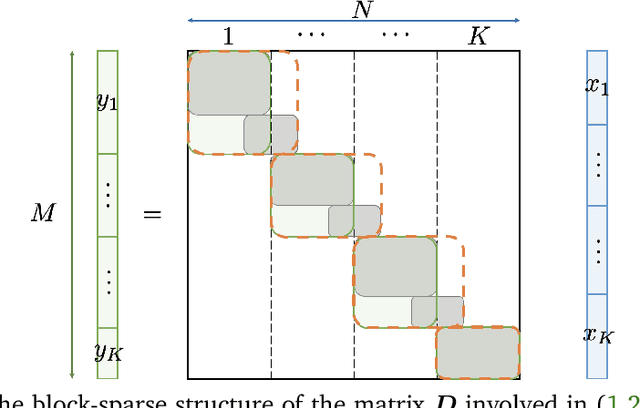
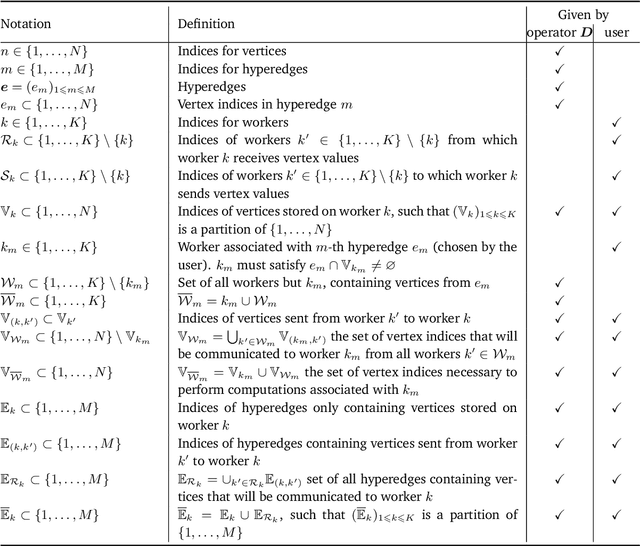
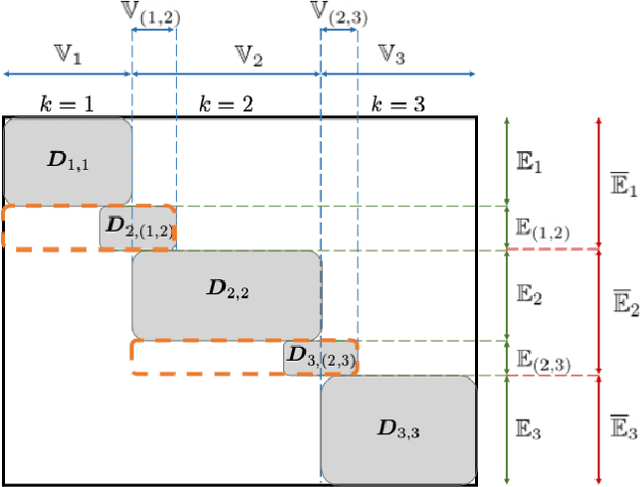
Sampling-based algorithms are classical approaches to perform Bayesian inference in inverse problems. They provide estimators with the associated credibility intervals to quantify the uncertainty on the estimators. Although these methods hardly scale to high dimensional problems, they have recently been paired with optimization techniques, such as proximal and splitting approaches, to address this issue. Such approaches pave the way to distributed samplers, splitting computations to make inference more scalable and faster. We introduce a distributed Gibbs sampler to efficiently solve such problems, considering posterior distributions with multiple smooth and non-smooth functions composed with linear operators. The proposed approach leverages a recent approximate augmentation technique reminiscent of primal-dual optimization methods. It is further combined with a block-coordinate approach to split the primal and dual variables into blocks, leading to a distributed block-coordinate Gibbs sampler. The resulting algorithm exploits the hypergraph structure of the involved linear operators to efficiently distribute the variables over multiple workers under controlled communication costs. It accommodates several distributed architectures, such as the Single Program Multiple Data and client-server architectures. Experiments on a large image deblurring problem show the performance of the proposed approach to produce high quality estimates with credibility intervals in a small amount of time.

Learning Maximally Monotone Operators for Image Recovery

We introduce a new paradigm for solving regularized variational problems. These are typically formulated to address ill-posed inverse problems encountered in signal and image processing. The objective function is traditionally defined by adding a regularization function to a data fit term, which is subsequently minimized by using iterative optimization algorithms. Recently, several works have proposed to replace the operator related to the regularization by a more sophisticated denoiser. These approaches, known as plug-and-play (PnP) methods, have shown excellent performance. Although it has been noticed that, under nonexpansiveness assumptions on the denoisers, the convergence of the resulting algorithm is guaranteed, little is known about characterizing the asymptotically delivered solution. In the current article, we propose to address this limitation. More specifically, instead of employing a functional regularization, we perform an operator regularization, where a maximally monotone operator (MMO) is learned in a supervised manner. This formulation is flexible as it allows the solution to be characterized through a broad range of variational inequalities, and it includes convex regularizations as special cases. From an algorithmic standpoint, the proposed approach consists in replacing the resolvent of the MMO by a neural network (NN). We provide a universal approximation theorem proving that nonexpansive NNs provide suitable models for the resolvent of a wide class of MMOs. The proposed approach thus provides a sound theoretical framework for analyzing the asymptotic behavior of first-order PnP algorithms. In addition, we propose a numerical strategy to train NNs corresponding to resolvents of MMOs. We apply our approach to image restoration problems and demonstrate its validity in terms of both convergence and quality.