Phare: A Safety Probe for Large Language Models

Ensuring the safety of large language models (LLMs) is critical for responsible deployment, yet existing evaluations often prioritize performance over identifying failure modes. We introduce Phare, a multilingual diagnostic framework to probe and evaluate LLM behavior across three critical dimensions: hallucination and reliability, social biases, and harmful content generation. Our evaluation of 17 state-of-the-art LLMs reveals patterns of systematic vulnerabilities across all safety dimensions, including sycophancy, prompt sensitivity, and stereotype reproduction. By highlighting these specific failure modes rather than simply ranking models, Phare provides researchers and practitioners with actionable insights to build more robust, aligned, and trustworthy language systems.

Analysis and Synthesis Denoisers for Forward-Backward Plug-and-Play Algorithms

In this work we study the behavior of the forward-backward (FB) algorithm when the proximity operator is replaced by a sub-iterative procedure to approximate a Gaussian denoiser, in a Plug-and-Play (PnP) fashion. In particular, we consider both analysis and synthesis Gaussian denoisers within a dictionary framework, obtained by unrolling dual-FB iterations or FB iterations, respectively. We analyze the associated minimization problems as well as the asymptotic behavior of the resulting FB-PnP iterations. In particular, we show that the synthesis Gaussian denoising problem can be viewed as a proximity operator. For each case, analysis and synthesis, we show that the FB-PnP algorithms solve the same problem whether we use only one or an infinite number of sub-iteration to solve the denoising problem at each iteration. To this aim, we show that each "one sub-iteration" strategy within the FB-PnP can be interpreted as a primal-dual algorithm when a warm-restart strategy is used. We further present similar results when using a Moreau-Yosida smoothing of the global problem, for an arbitrary number of sub-iterations. Finally, we provide numerical simulations to illustrate our theoretical results. In particular we first consider a toy compressive sensing example, as well as an image restoration problem in a deep dictionary framework.

Sliced-Wasserstein on Symmetric Positive Definite Matrices for M/EEG Signals

When dealing with electro or magnetoencephalography records, many supervised prediction tasks are solved by working with covariance matrices to summarize the signals. Learning with these matrices requires using Riemanian geometry to account for their structure. In this paper, we propose a new method to deal with distributions of covariance matrices and demonstrate its computational efficiency on M/EEG multivariate time series. More specifically, we define a Sliced-Wasserstein distance between measures of symmetric positive definite matrices that comes with strong theoretical guarantees. Then, we take advantage of its properties and kernel methods to apply this distance to brain-age prediction from MEG data and compare it to state-of-the-art algorithms based on Riemannian geometry. Finally, we show that it is an efficient surrogate to the Wasserstein distance in domain adaptation for Brain Computer Interface applications.

Dictionary and prior learning with unrolled algorithms for unsupervised inverse problems

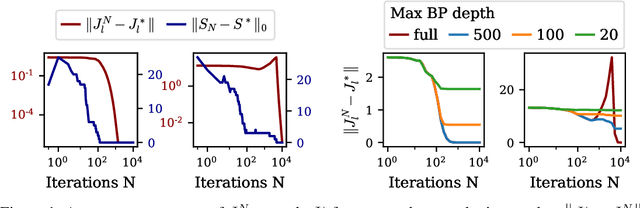
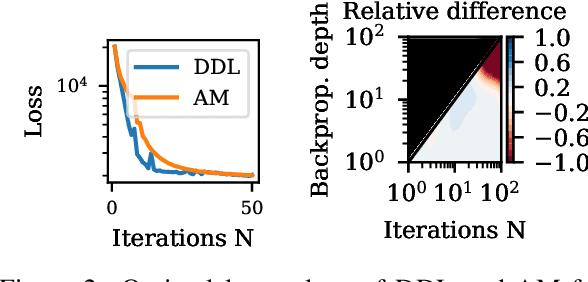
Inverse problems consist in recovering a signal given noisy observations. One classical resolution approach is to leverage sparsity and integrate prior knowledge of the signal to the reconstruction algorithm to get a plausible solution. Still, this prior might not be sufficiently adapted to the data. In this work, we study Dictionary and Prior learning from degraded measurements as a bi-level problem, and we take advantage of unrolled algorithms to solve approximate formulations of Synthesis and Analysis. We provide an empirical and theoretical analysis of automatic differentiation for Dictionary Learning to understand better the pros and cons of unrolling in this context. We find that unrolled algorithms speed up the recovery process for a small number of iterations by improving the gradient estimation. Then we compare Analysis and Synthesis by evaluating the performance of unrolled algorithms for inverse problems, without access to any ground truth data for several classes of dictionaries and priors. While Analysis can achieve good results,Synthesis is more robust and performs better. Finally, we illustrate our method on pattern and structure learning tasks from degraded measurements.