Aitchison Geometry on the Simplex for Uncertainty Quantification in Bayesian Hyperspectral Image Unmixing

Most algorithms for hyperspectral image unmixing produce point estimates of fractional abundances of the materials to be separated. However, in the absence of reliable ground truth, the ability to perform abundance uncertainty quantification (UQ) should be an important feature of algorithms, e.g. to evaluate how hard the unmixing problem is and how much the results should be trusted. The usual modeling assumptions in Bayesian models for unmixing rely heavily on the Euclidean geometry of the simplex and typically disregard spatial information. In addition, to our knowledge, abundance UQ is close to nonexistent. In this paper, we propose to leverage Aitchinson geometry from the compositional data analysis literature to provide practitioners with alternative tools for modeling prior abundance distributions. In particular we show how to design simplex-valued Gaussian Process priors using this geometry. Then we link Aitchinson geometry to constrained sampling algorithms in the literature, and propose UQ diagnostics that comply with the constraints on abundance vectors. We illustrate these concepts on real and simulated data.

Static and auto-regressive neural emulation of phytoplankton biomass dynamics from physical predictors in the global ocean

Phytoplankton is the basis of marine food webs, driving both ecological processes and global biogeochemical cycles. Despite their ecological and climatic significance, accurately simulating phytoplankton dynamics remains a major challenge for biogeochemical numerical models due to limited parameterizations, sparse observational data, and the complexity of oceanic processes. Here, we explore how deep learning models can be used to address these limitations predicting the spatio-temporal distribution of phytoplankton biomass in the global ocean based on satellite observations and environmental conditions. First, we investigate several deep learning architectures. Among the tested models, the UNet architecture stands out for its ability to reproduce the seasonal and interannual patterns of phytoplankton biomass more accurately than other models like CNNs, ConvLSTM, and 4CastNet. When using one to two months of environmental data as input, UNet performs better, although it tends to underestimate the amplitude of low-frequency changes in phytoplankton biomass. Thus, to improve predictions over time, an auto-regressive version of UNet was also tested, where the model uses its own previous predictions to forecast future conditions. This approach works well for short-term forecasts (up to five months), though its performance decreases for longer time scales. Overall, our study shows that combining ocean physical predictors with deep learning allows for reconstruction and short-term prediction of phytoplankton dynamics. These models could become powerful tools for monitoring ocean health and supporting marine ecosystem management, especially in the context of climate change.

Discovering Data Manifold Geometry via Non-Contracting Flows

We introduce an unsupervised approach for constructing a global reference system by learning, in the ambient space, vector fields that span the tangent spaces of an unknown data manifold. In contrast to isometric objectives, which implicitly assume manifold flatness, our method learns tangent vector fields whose flows transport all samples to a common, learnable reference point. The resulting arc-lengths along these flows define interpretable intrinsic coordinates tied to a shared global frame. To prevent degenerate collapse, we enforce a non-shrinking constraint and derive a scalable, integration-free objective inspired by flow matching. Within our theoretical framework, we prove that minimizing the proposed objective recovers a global coordinate chart when one exists. Empirically, we obtain correct tangent alignment and coherent global coordinate structure on synthetic manifolds. We also demonstrate the scalability of our method on CIFAR-10, where the learned coordinates achieve competitive downstream classification performance.

Busemann Functions in the Wasserstein Space: Existence, Closed-Forms, and Applications to Slicing

The Busemann function has recently found much interest in a variety of geometric machine learning problems, as it naturally defines projections onto geodesic rays of Riemannian manifolds and generalizes the notion of hyperplanes. As several sources of data can be conveniently modeled as probability distributions, it is natural to study this function in the Wasserstein space, which carries a rich formal Riemannian structure induced by Optimal Transport metrics. In this work, we investigate the existence and computation of Busemann functions in Wasserstein space, which admits geodesic rays. We establish closed-form expressions in two important cases: one-dimensional distributions and Gaussian measures. These results enable explicit projection schemes for probability distributions on $\mathbb{R}$, which in turn allow us to define novel Sliced-Wasserstein distances over Gaussian mixtures and labeled datasets. We demonstrate the efficiency of those original schemes on synthetic datasets as well as transfer learning problems.

Anomalous Samples for Few-Shot Anomaly Detection

Several anomaly detection and classification methods rely on large amounts of non-anomalous or "normal" samples under the assump- tion that anomalous data is typically harder to acquire. This hypothesis becomes questionable in Few-Shot settings, where as little as one anno- tated sample can make a significant difference. In this paper, we tackle the question of utilizing anomalous samples in training a model for bi- nary anomaly classification. We propose a methodology that incorporates anomalous samples in a multi-score anomaly detection score leveraging recent Zero-Shot and memory-based techniques. We compare the utility of anomalous samples to that of regular samples and study the benefits and limitations of each. In addition, we propose an augmentation-based validation technique to optimize the aggregation of the different anomaly scores and demonstrate its effectiveness on popular industrial anomaly detection datasets.

Object-Centric Cropping for Visual Few-Shot Classification

In the domain of Few-Shot Image Classification, operating with as little as one example per class, the presence of image ambiguities stemming from multiple objects or complex backgrounds can significantly deteriorate performance. Our research demonstrates that incorporating additional information about the local positioning of an object within its image markedly enhances classification across established benchmarks. More importantly, we show that a significant fraction of the improvement can be achieved through the use of the Segment Anything Model, requiring only a pixel of the object of interest to be pointed out, or by employing fully unsupervised foreground object extraction methods.

Augmented Invertible Koopman Autoencoder for long-term time series forecasting

Following the introduction of Dynamic Mode Decomposition and its numerous extensions, many neural autoencoder-based implementations of the Koopman operator have recently been proposed. This class of methods appears to be of interest for modeling dynamical systems, either through direct long-term prediction of the evolution of the state or as a powerful embedding for downstream methods. In particular, a recent line of work has developed invertible Koopman autoencoders (IKAEs), which provide an exact reconstruction of the input state thanks to their analytically invertible encoder, based on coupling layer normalizing flow models. We identify that the conservation of the dimension imposed by the normalizing flows is a limitation for the IKAE models, and thus we propose to augment the latent state with a second, non-invertible encoder network. This results in our new model: the Augmented Invertible Koopman AutoEncoder (AIKAE). We demonstrate the relevance of the AIKAE through a series of long-term time series forecasting experiments, on satellite image time series as well as on a benchmark involving predictions based on a large lookback window of observations.

FlowKac: An Efficient Neural Fokker-Planck solver using Temporal Normalizing flows and the Feynman Kac-Formula

Solving the Fokker-Planck equation for high-dimensional complex dynamical systems remains a pivotal yet challenging task due to the intractability of analytical solutions and the limitations of traditional numerical methods. In this work, we present FlowKac, a novel approach that reformulates the Fokker-Planck equation using the Feynman-Kac formula, allowing to query the solution at a given point via the expected values of stochastic paths. A key innovation of FlowKac lies in its adaptive stochastic sampling scheme which significantly reduces the computational complexity while maintaining high accuracy. This sampling technique, coupled with a time-indexed normalizing flow, designed for capturing time-evolving probability densities, enables robust sampling of collocation points, resulting in a flexible and mesh-free solver. This formulation mitigates the curse of dimensionality and enhances computational efficiency and accuracy, which is particularly crucial for applications that inherently require dimensions beyond the conventional three. We validate the robustness and scalability of our method through various experiments on a range of stochastic differential equations, demonstrating significant improvements over existing techniques.

Land Surface Temperature Super-Resolution with a Scale-Invariance-Free Neural Approach: Application to MODIS

Due to the trade-off between the temporal and spatial resolution of thermal spaceborne sensors, super-resolution methods have been developed to provide fine-scale Land SurfaceTemperature (LST) maps. Most of them are trained at low resolution but applied at fine resolution, and so they require a scale-invariance hypothesis that is not always adapted. Themain contribution of this work is the introduction of a Scale-Invariance-Free approach for training Neural Network (NN) models, and the implementation of two NN models, calledScale-Invariance-Free Convolutional Neural Network for Super-Resolution (SIF-CNN-SR) for the super-resolution of MODIS LST products. The Scale-Invariance-Free approach consists ontraining the models in order to provide LST maps at high spatial resolution that recover the initial LST when they are degraded at low resolution and that contain fine-scale texturesinformed by the high resolution NDVI. The second contribution of this work is the release of a test database with ASTER LST images concomitant with MODIS ones that can be usedfor evaluation of super-resolution algorithms. We compare the two proposed models, SIF-CNN-SR1 and SIF-CNN-SR2, with four state-of-the-art methods, Bicubic, DMS, ATPRK, Tsharp,and a CNN sharing the same architecture as SIF-CNN-SR but trained under the scale-invariance hypothesis. We show that SIF-CNN-SR1 outperforms the state-of-the-art methods and the other two CNN models as evaluated with LPIPS and Fourier space metrics focusing on the analysis of textures. These results and the available ASTER-MODIS database for evaluation are promising for future studies on super-resolution of LST.

Koopman Ensembles for Probabilistic Time Series Forecasting

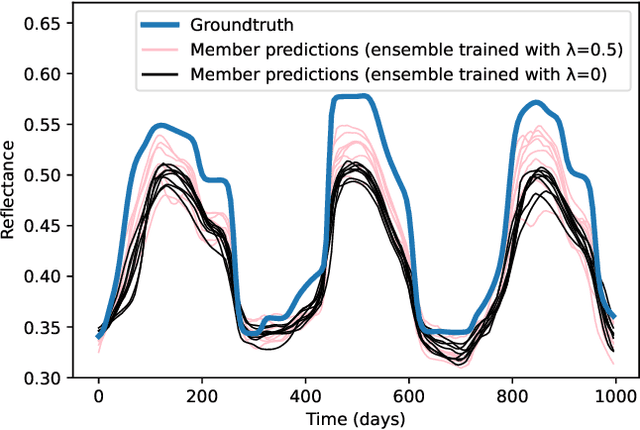
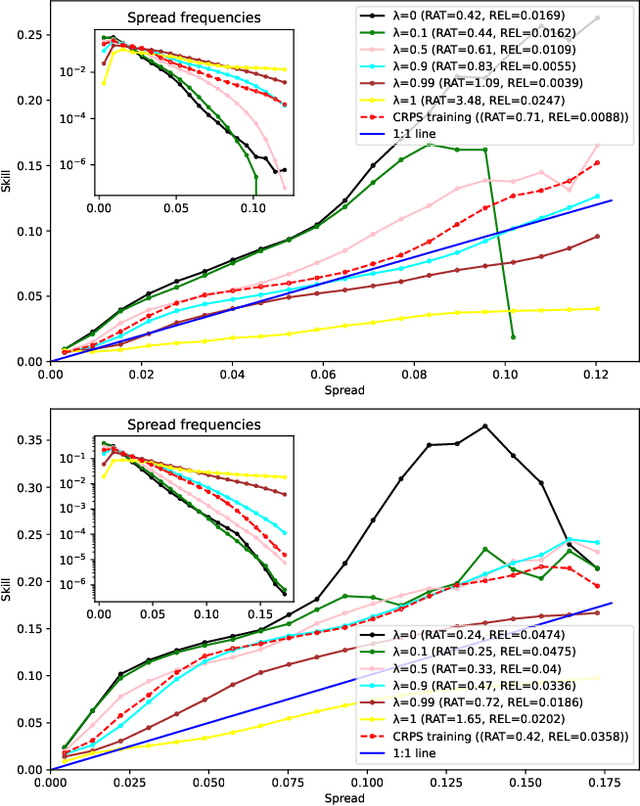
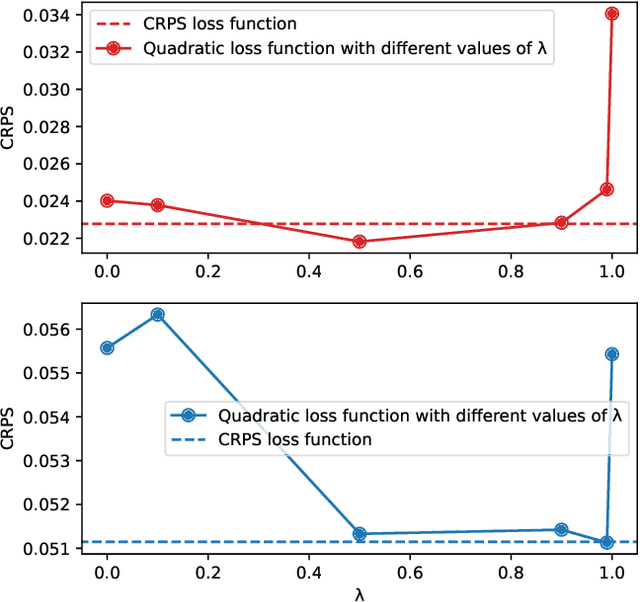
In the context of an increasing popularity of data-driven models to represent dynamical systems, many machine learning-based implementations of the Koopman operator have recently been proposed. However, the vast majority of those works are limited to deterministic predictions, while the knowledge of uncertainty is critical in fields like meteorology and climatology. In this work, we investigate the training of ensembles of models to produce stochastic outputs. We show through experiments on real remote sensing image time series that ensembles of independently trained models are highly overconfident and that using a training criterion that explicitly encourages the members to produce predictions with high inter-model variances greatly improves the uncertainty quantification of the ensembles.