FlowKac: An Efficient Neural Fokker-Planck solver using Temporal Normalizing flows and the Feynman Kac-Formula

Solving the Fokker-Planck equation for high-dimensional complex dynamical systems remains a pivotal yet challenging task due to the intractability of analytical solutions and the limitations of traditional numerical methods. In this work, we present FlowKac, a novel approach that reformulates the Fokker-Planck equation using the Feynman-Kac formula, allowing to query the solution at a given point via the expected values of stochastic paths. A key innovation of FlowKac lies in its adaptive stochastic sampling scheme which significantly reduces the computational complexity while maintaining high accuracy. This sampling technique, coupled with a time-indexed normalizing flow, designed for capturing time-evolving probability densities, enables robust sampling of collocation points, resulting in a flexible and mesh-free solver. This formulation mitigates the curse of dimensionality and enhances computational efficiency and accuracy, which is particularly crucial for applications that inherently require dimensions beyond the conventional three. We validate the robustness and scalability of our method through various experiments on a range of stochastic differential equations, demonstrating significant improvements over existing techniques.

Time-changed normalizing flows for accurate SDE modeling

The generative paradigm has become increasingly important in machine learning and deep learning models. Among popular generative models are normalizing flows, which enable exact likelihood estimation by transforming a base distribution through diffeomorphic transformations. Extending the normalizing flow framework to handle time-indexed flows gave dynamic normalizing flows, a powerful tool to model time series, stochastic processes, and neural stochastic differential equations (SDEs). In this work, we propose a novel variant of dynamic normalizing flows, a Time Changed Normalizing Flow (TCNF), based on time deformation of a Brownian motion which constitutes a versatile and extensive family of Gaussian processes. This approach enables us to effectively model some SDEs, that cannot be modeled otherwise, including standard ones such as the well-known Ornstein-Uhlenbeck process, and generalizes prior methodologies, leading to improved results and better inference and prediction capability.

Geometry-preserving lie group integrators for differential equations on the manifold of symmetric positive definite matrices

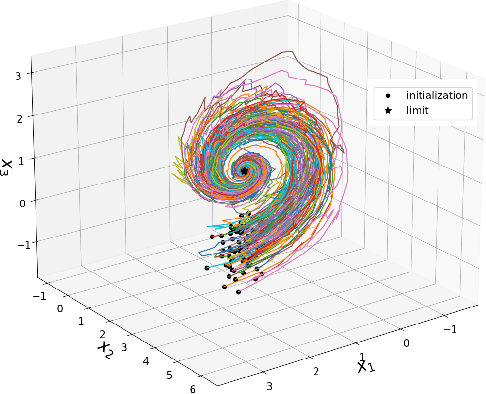
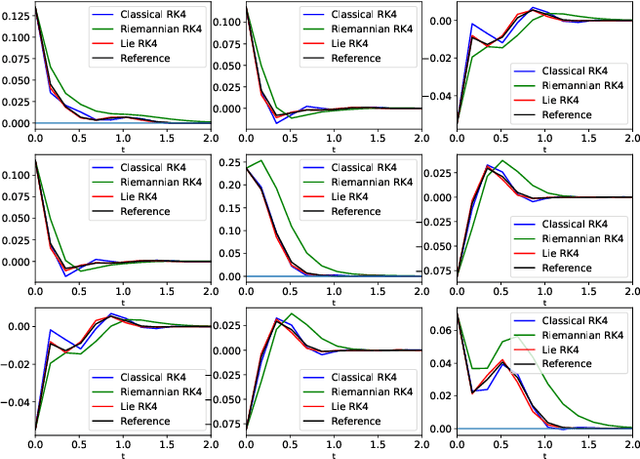
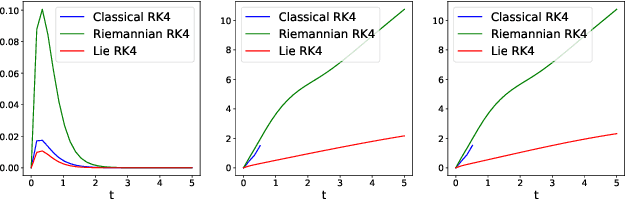
In many applications, one encounters signals that lie on manifolds rather than a Euclidean space. In particular, covariance matrices are examples of ubiquitous mathematical objects that have a non Euclidean structure. The application of Euclidean methods to integrate differential equations lying on such objects does not respect the geometry of the manifold, which can cause many numerical issues. In this paper, we propose to use Lie group methods to define geometry-preserving numerical integration schemes on the manifold of symmetric positive definite matrices. These can be applied to a number of differential equations on covariance matrices of practical interest. We show that they are more stable and robust than other classical or naive integration schemes on an example.