Online Learning of Weakly Coupled MDP Policies for Load Balancing and Auto Scaling

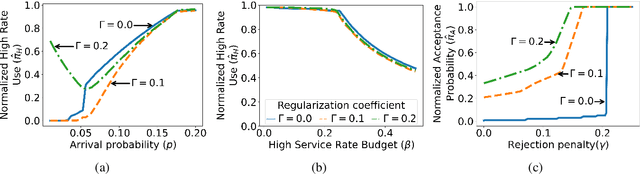
Load balancing and auto scaling are at the core of scalable, contemporary systems, addressing dynamic resource allocation and service rate adjustments in response to workload changes. This paper introduces a novel model and algorithms for tuning load balancers coupled with auto scalers, considering bursty traffic arriving at finite queues. We begin by presenting the problem as a weakly coupled Markov Decision Processes (MDP), solvable via a linear program (LP). However, as the number of control variables of such LP grows combinatorially, we introduce a more tractable relaxed LP formulation, and extend it to tackle the problem of online parameter learning and policy optimization using a two-timescale algorithm based on the LP Lagrangian.

A Practical Approach to Novel Class Discovery in Tabular Data

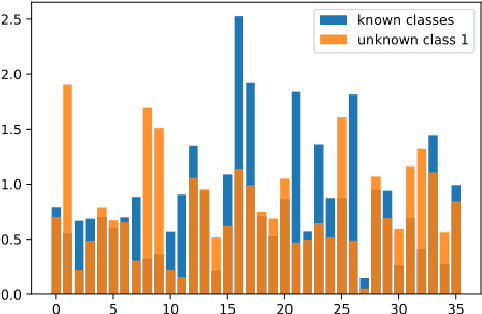
The problem of Novel Class Discovery (NCD) consists in extracting knowledge from a labeled set of known classes to accurately partition an unlabeled set of novel classes. While NCD has recently received a lot of attention from the community, it is often solved on computer vision problems and under unrealistic conditions. In particular, the number of novel classes is usually assumed to be known in advance, and their labels are sometimes used to tune hyperparameters. Methods that rely on these assumptions are not applicable in real-world scenarios. In this work, we focus on solving NCD in tabular data when no prior knowledge of the novel classes is available. To this end, we propose to tune the hyperparameters of NCD methods by adapting the $k$-fold cross-validation process and hiding some of the known classes in each fold. Since we have found that methods with too many hyperparameters are likely to overfit these hidden classes, we define a simple deep NCD model. This method is composed of only the essential elements necessary for the NCD problem and performs impressively well under realistic conditions. Furthermore, we find that the latent space of this method can be used to reliably estimate the number of novel classes. Additionally, we adapt two unsupervised clustering algorithms ($k$-means and Spectral Clustering) to leverage the knowledge of the known classes. Extensive experiments are conducted on 7 tabular datasets and demonstrate the effectiveness of the proposed method and hyperparameter tuning process, and show that the NCD problem can be solved without relying on knowledge from the novel classes.

An Interactive Interface for Novel Class Discovery in Tabular Data

Novel Class Discovery (NCD) is the problem of trying to discover novel classes in an unlabeled set, given a labeled set of different but related classes. The majority of NCD methods proposed so far only deal with image data, despite tabular data being among the most widely used type of data in practical applications. To interpret the results of clustering or NCD algorithms, data scientists need to understand the domain- and application-specific attributes of tabular data. This task is difficult and can often only be performed by a domain expert. Therefore, this interface allows a domain expert to easily run state-of-the-art algorithms for NCD in tabular data. With minimal knowledge in data science, interpretable results can be generated.

Online Learning with Adversaries: A Differential Inclusion Analysis

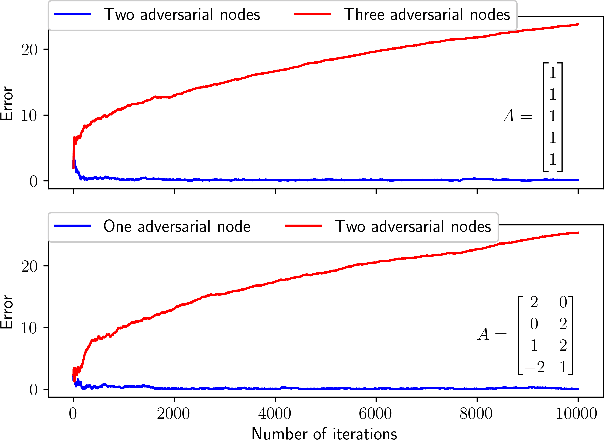
We consider the measurement model $Y = AX,$ where $X$ and, hence, $Y$ are random variables and $A$ is an a priori known tall matrix. At each time instance, a sample of one of $Y$'s coordinates is available, and the goal is to estimate $\mu := \mathbb{E}[X]$ via these samples. However, the challenge is that a small but unknown subset of $Y$'s coordinates are controlled by adversaries with infinite power: they can return any real number each time they are queried for a sample. For such an adversarial setting, we propose the first asynchronous online algorithm that converges to $\mu$ almost surely. We prove this result using a novel differential inclusion based two-timescale analysis. Two key highlights of our proof include: (a) the use of a novel Lyapunov function for showing that $\mu$ is the unique global attractor for our algorithm's limiting dynamics, and (b) the use of martingale and stopping time theory to show that our algorithm's iterates are almost surely bounded.

Novel Class Discovery: an Introduction and Key Concepts

Novel Class Discovery (NCD) is a growing field where we are given during training a labeled set of known classes and an unlabeled set of different classes that must be discovered. In recent years, many methods have been proposed to address this problem, and the field has begun to mature. In this paper, we provide a comprehensive survey of the state-of-the-art NCD methods. We start by formally defining the NCD problem and introducing important notions. We then give an overview of the different families of approaches, organized by the way they transfer knowledge from the labeled set to the unlabeled set. We find that they either learn in two stages, by first extracting knowledge from the labeled data only and then applying it to the unlabeled data, or in one stage by conjointly learning on both sets. For each family, we describe their general principle and detail a few representative methods. Then, we briefly introduce some new related tasks inspired by the increasing number of NCD works. We also present some common tools and techniques used in NCD, such as pseudo labeling, self-supervised learning and contrastive learning. Finally, to help readers unfamiliar with the NCD problem differentiate it from other closely related domains, we summarize some of the closest areas of research and discuss their main differences.

Découvrir de nouvelles classes dans des données tabulaires

In Novel Class Discovery (NCD), the goal is to find new classes in an unlabeled set given a labeled set of known but different classes. While NCD has recently gained attention from the community, no framework has yet been proposed for heterogeneous tabular data, despite being a very common representation of data. In this paper, we propose TabularNCD, a new method for discovering novel classes in tabular data. We show a way to extract knowledge from already known classes to guide the discovery process of novel classes in the context of tabular data which contains heterogeneous variables. A part of this process is done by a new method for defining pseudo labels, and we follow recent findings in Multi-Task Learning to optimize a joint objective function. Our method demonstrates that NCD is not only applicable to images but also to heterogeneous tabular data.

Geometry-preserving lie group integrators for differential equations on the manifold of symmetric positive definite matrices

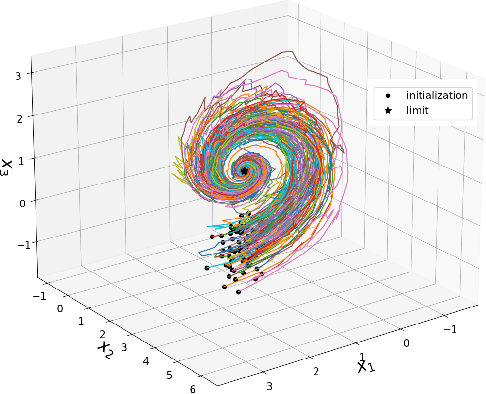
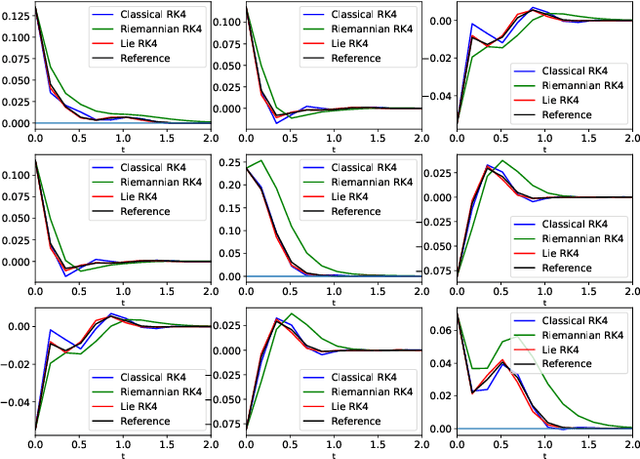
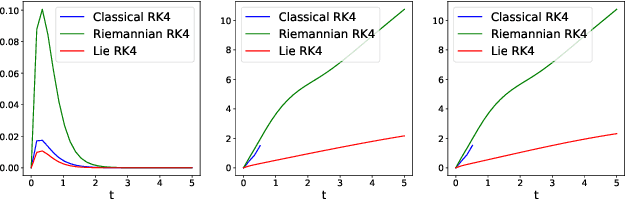
In many applications, one encounters signals that lie on manifolds rather than a Euclidean space. In particular, covariance matrices are examples of ubiquitous mathematical objects that have a non Euclidean structure. The application of Euclidean methods to integrate differential equations lying on such objects does not respect the geometry of the manifold, which can cause many numerical issues. In this paper, we propose to use Lie group methods to define geometry-preserving numerical integration schemes on the manifold of symmetric positive definite matrices. These can be applied to a number of differential equations on covariance matrices of practical interest. We show that they are more stable and robust than other classical or naive integration schemes on an example.

Online Multi-Agent Decentralized Byzantine-robust Gradient Estimation

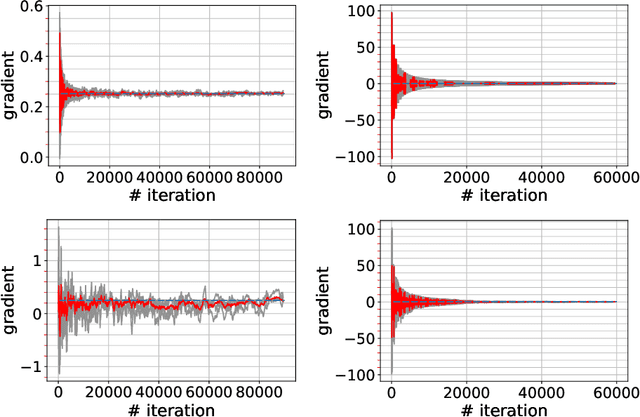
In this paper, we propose an iterative scheme for distributed Byzantineresilient estimation of a gradient associated with a black-box model. Our algorithm is based on simultaneous perturbation, secure state estimation and two-timescale stochastic approximations. We also show the performance of our algorithm through numerical experiments.

A Method for Discovering Novel Classes in Tabular Data

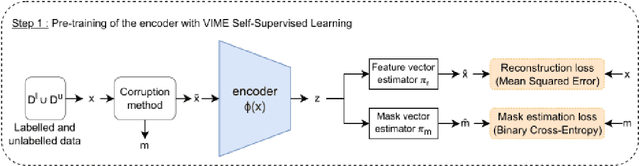
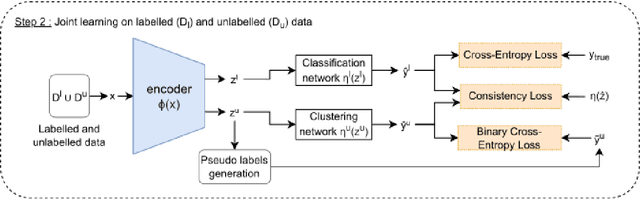
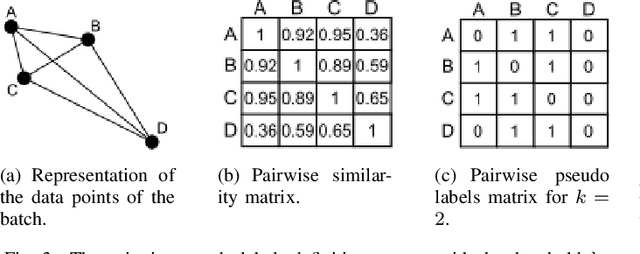
In Novel Class Discovery (NCD), the goal is to find new classes in an unlabeled set given a labeled set of known but different classes. While NCD has recently gained attention from the community, no framework has yet been proposed for heterogeneous tabular data, despite being a very common representation of data. In this paper, we propose TabularNCD, a new method for discovering novel classes in tabular data. We show a way to extract knowledge from already known classes to guide the discovery process of novel classes in the context of tabular data which contains heterogeneous variables. A part of this process is done by a new method for defining pseudo labels, and we follow recent findings in Multi-Task Learning to optimize a joint objective function. Our method demonstrates that NCD is not only applicable to images but also to heterogeneous tabular data. Extensive experiments are conducted to evaluate our method and demonstrate its effectiveness against 3 competitors on 7 diverse public classification datasets.

Opinion shaping in social networks using reinforcement learning

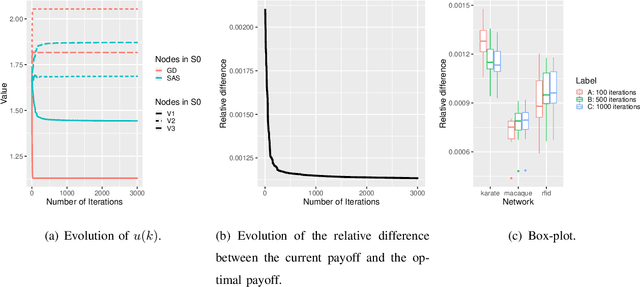
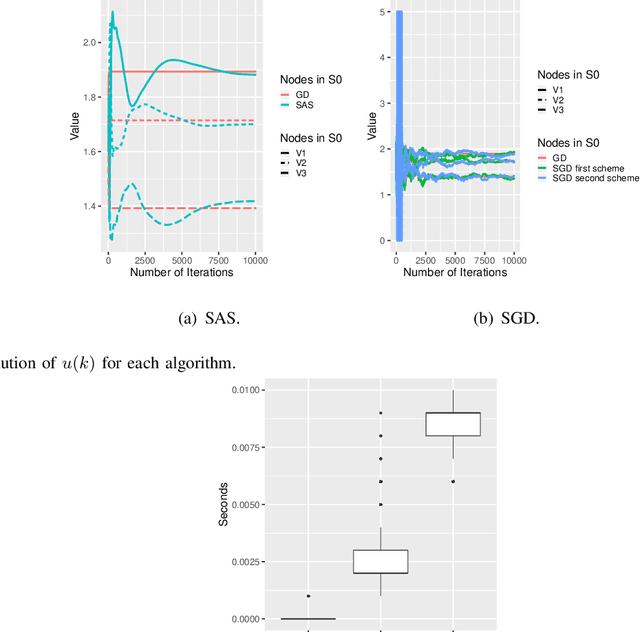
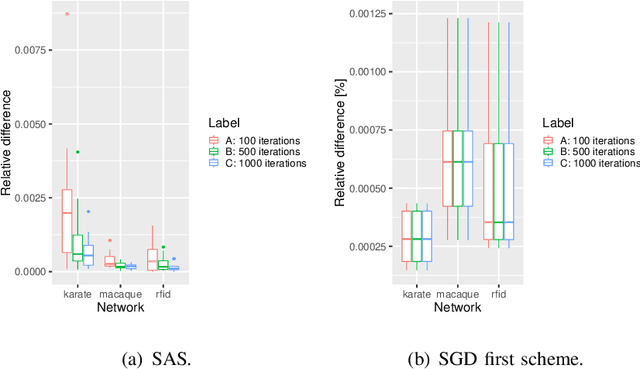
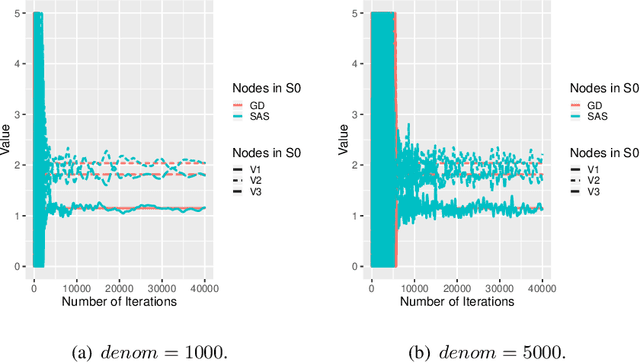
In this paper, we study how to shape opinions in social networks when the matrix of interactions is unknown. We consider classical opinion dynamics with some stubborn agents and the possibility of continuously influencing the opinions of a few selected agents, albeit under resource constraints. We map the opinion dynamics to a value iteration scheme for policy evaluation for a specific stochastic shortest path problem. This leads to a representation of the opinion vector as an approximate value function for a stochastic shortest path problem with some non-classical constraints. We suggest two possible ways of influencing agents. One leads to a convex optimization problem and the other to a non-convex one. Firstly, for both problems, we propose two different online two-time scale reinforcement learning schemes that converge to the optimal solution of each problem. Secondly, we suggest stochastic gradient descent schemes and compare these classes of algorithms with the two-time scale reinforcement learning schemes. Thirdly, we also derive another algorithm designed to tackle the curse of dimensionality one faces when all agents are observed. Numerical studies are provided to illustrate the convergence and efficiency of our algorithms.