Reliable Policy Iteration: Performance Robustness Across Architecture and Environment Perturbations

In a recent work, we proposed Reliable Policy Iteration (RPI), that restores policy iteration's monotonicity-of-value-estimates property to the function approximation setting. Here, we assess the robustness of RPI's empirical performance on two classical control tasks -- CartPole and Inverted Pendulum -- under changes to neural network and environmental parameters. Relative to DQN, Double DQN, DDPG, TD3, and PPO, RPI reaches near-optimal performance early and sustains this policy as training proceeds. Because deep RL methods are often hampered by sample inefficiency, training instability, and hyperparameter sensitivity, our results highlight RPI's promise as a more reliable alternative.

Reinforcement Learning with Quasi-Hyperbolic Discounting

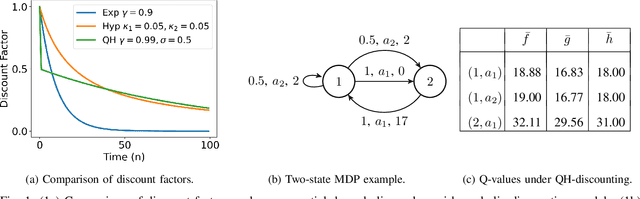
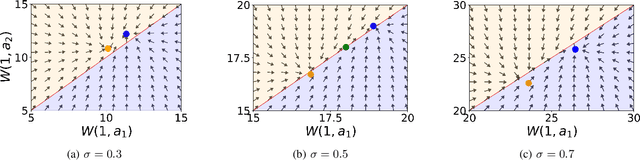
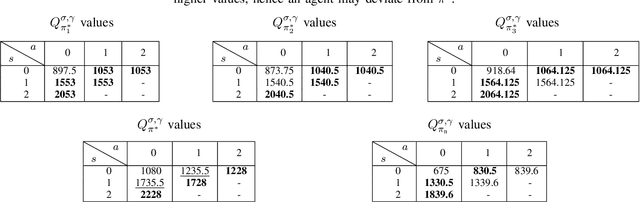
Reinforcement learning has traditionally been studied with exponential discounting or the average reward setup, mainly due to their mathematical tractability. However, such frameworks fall short of accurately capturing human behavior, which has a bias towards immediate gratification. Quasi-Hyperbolic (QH) discounting is a simple alternative for modeling this bias. Unlike in traditional discounting, though, the optimal QH-policy, starting from some time $t_1,$ can be different to the one starting from $t_2.$ Hence, the future self of an agent, if it is naive or impatient, can deviate from the policy that is optimal at the start, leading to sub-optimal overall returns. To prevent this behavior, an alternative is to work with a policy anchored in a Markov Perfect Equilibrium (MPE). In this work, we propose the first model-free algorithm for finding an MPE. Using a two-timescale analysis, we show that, if our algorithm converges, then the limit must be an MPE. We also validate this claim numerically for the standard inventory system with stochastic demands. Our work significantly advances the practical application of reinforcement learning.

Online Learning of Weakly Coupled MDP Policies for Load Balancing and Auto Scaling

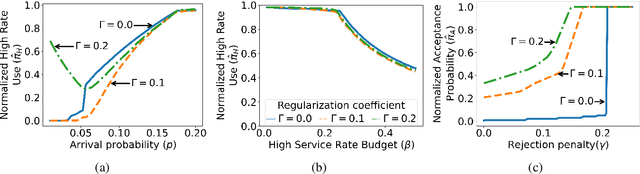
Load balancing and auto scaling are at the core of scalable, contemporary systems, addressing dynamic resource allocation and service rate adjustments in response to workload changes. This paper introduces a novel model and algorithms for tuning load balancers coupled with auto scalers, considering bursty traffic arriving at finite queues. We begin by presenting the problem as a weakly coupled Markov Decision Processes (MDP), solvable via a linear program (LP). However, as the number of control variables of such LP grows combinatorially, we introduce a more tractable relaxed LP formulation, and extend it to tackle the problem of online parameter learning and policy optimization using a two-timescale algorithm based on the LP Lagrangian.