Early Classification of Time Series in Non-Stationary Cost Regimes

Early Classification of Time Series (ECTS) addresses decision-making problems in which predictions must be made as early as possible while maintaining high accuracy. Most existing ECTS methods assume that the time-dependent decision costs governing the learning objective are known, fixed, and correctly specified. In practice, however, these costs are often uncertain and may change over time, leading to mismatches between training-time and deployment-time objectives. In this paper, we study ECTS under two practically relevant forms of cost non-stationarity: drift in the balance between misclassification and decision delay costs, and stochastic realizations of decision costs that deviate from the nominal training-time model. To address these challenges, we revisit representative ECTS approaches and adapt them to an online learning setting. Focusing on separable methods, we update only the triggering model during deployment, while keeping the classifier fixed. We propose several online adaptations and baselines, including bandit-based and RL-based approaches, and conduct controlled experiments on synthetic data to systematically evaluate robustness under cost non-stationarity. Our results demonstrate that online learning can effectively improve the robustness of ECTS methods to cost drift, with RL-based strategies exhibiting strong and stable performance across varying cost regimes.

Temporal Sepsis Modeling: a Fully Interpretable Relational Way

Sepsis remains one of the most complex and heterogeneous syndromes in intensive care, characterized by diverse physiological trajectories and variable responses to treatment. While deep learning models perform well in the early prediction of sepsis, they often lack interpretability and ignore latent patient sub-phenotypes. In this work, we propose a machine learning framework by opening up a new avenue for addressing this issue: a relational approach. Temporal data from electronic medical records (EMRs) are viewed as multivariate patient logs and represented in a relational data schema. Then, a propositionalisation technique (based on classic aggregation/selection functions from the field of relational data) is applied to construct interpretable features to "flatten" the data. Finally, the flattened data is classified using a selective naive Bayesian classifier. Experimental validation demonstrates the relevance of the suggested approach as well as its extreme interpretability. The interpretation is fourfold: univariate, global, local, and counterfactual.

On Forgetting and Stability of Score-based Generative models

Understanding the stability and long-time behavior of generative models is a fundamental problem in modern machine learning. This paper provides quantitative bounds on the sampling error of score-based generative models by leveraging stability and forgetting properties of the Markov chain associated with the reverse-time dynamics. Under weak assumptions, we provide the two structural properties to ensure the propagation of initialization and discretization errors of the backward process: a Lyapunov drift condition and a Doeblin-type minorization condition. A practical consequence is quantitative stability of the sampling procedure, as the reverse diffusion dynamics induces a contraction mechanism along the sampling trajectory. Our results clarify the role of stochastic dynamics in score-based models and provide a principled framework for analyzing propagation of errors in such approaches.

Deep Reinforcement Learning based Triggering Function for Early Classifiers of Time Series

Early Classification of Time Series (ECTS) has been recognized as an important problem in many areas where decisions have to be taken as soon as possible, before the full data availability, while time pressure increases. Numerous ECTS approaches have been proposed, based on different triggering functions, each taking into account various pieces of information related to the incoming time series and/or the output of a classifier. Although their performances have been empirically compared in the literature, no studies have been carried out on the optimality of these triggering functions that involve ``man-tailored'' decision rules. Based on the same information, could there be better triggering functions? This paper presents one way to investigate this question by showing first how to translate ECTS problems into Reinforcement Learning (RL) ones, where the very same information is used in the state space. A thorough comparison of the performance obtained by ``handmade'' approaches and their ``RL-based'' counterparts has been carried out. A second question investigated in this paper is whether a different combination of information, defining the state space in RL systems, can achieve even better performance. Experiments show that the system we describe, called \textsc{Alert}, significantly outperforms its state-of-the-art competitors on a large number of datasets.

Unsupervised Feature Construction for Anomaly Detection in Time Series -- An Evaluation

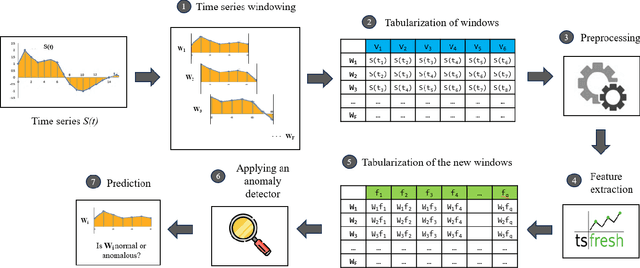
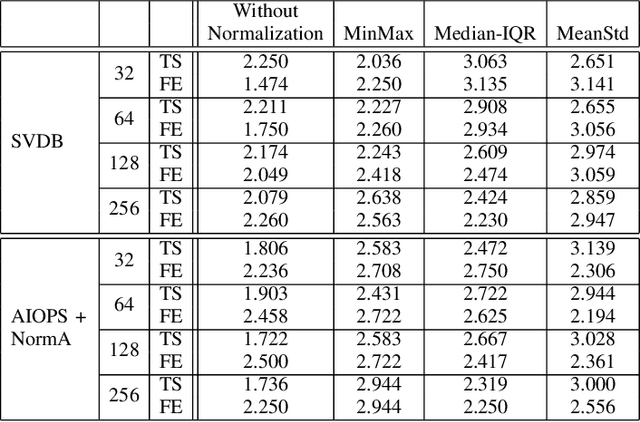
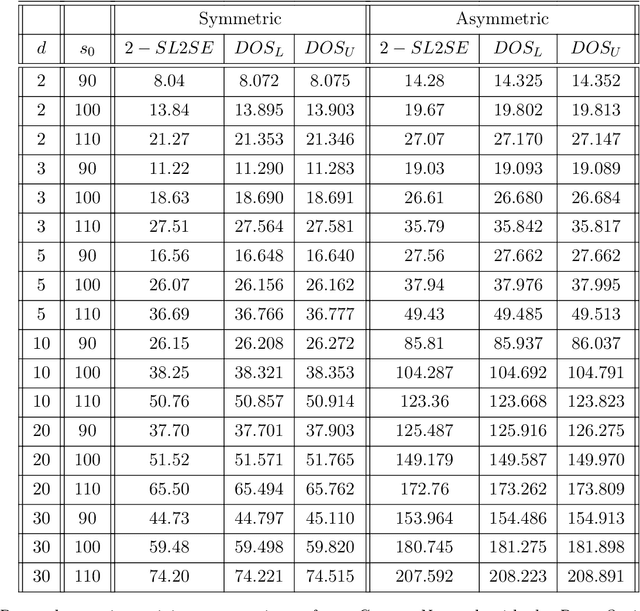
To detect anomalies with precision and without prior knowledge in time series, is it better to build a detector from the initial temporal representation, or to compute a new (tabular) representation using an existing automatic variable construction library? In this article, we address this question by conducting an in-depth experimental study for two popular detectors (Isolation Forest and Local Outlier Factor). The obtained results, for 5 different datasets, show that the new representation, computed using the tsfresh library, allows Isolation Forest to significantly improve its performance.

A new Input Convex Neural Network with application to options pricing

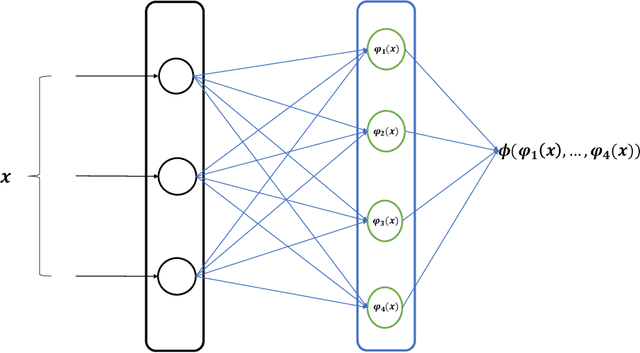
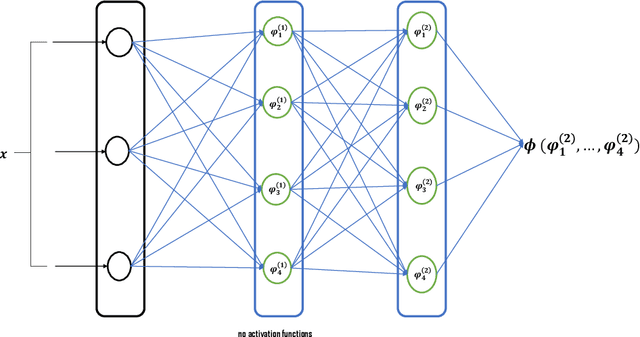
We introduce a new class of neural networks designed to be convex functions of their inputs, leveraging the principle that any convex function can be represented as the supremum of the affine functions it dominates. These neural networks, inherently convex with respect to their inputs, are particularly well-suited for approximating the prices of options with convex payoffs. We detail the architecture of this, and establish theoretical convergence bounds that validate its approximation capabilities. We also introduce a \emph{scrambling} phase to improve the training of these networks. Finally, we demonstrate numerically the effectiveness of these networks in estimating prices for three types of options with convex payoffs: Basket, Bermudan, and Swing options.

Mislabeled examples detection viewed as probing machine learning models: concepts, survey and extensive benchmark

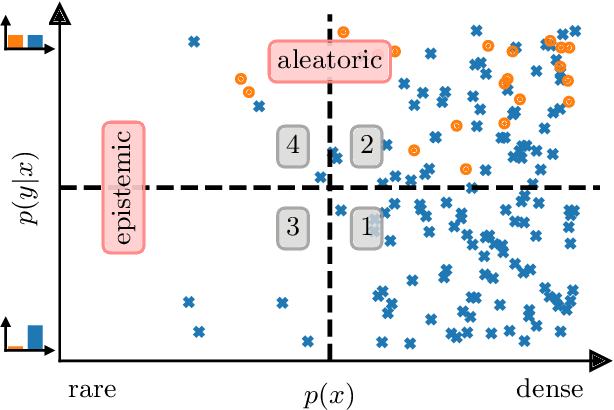
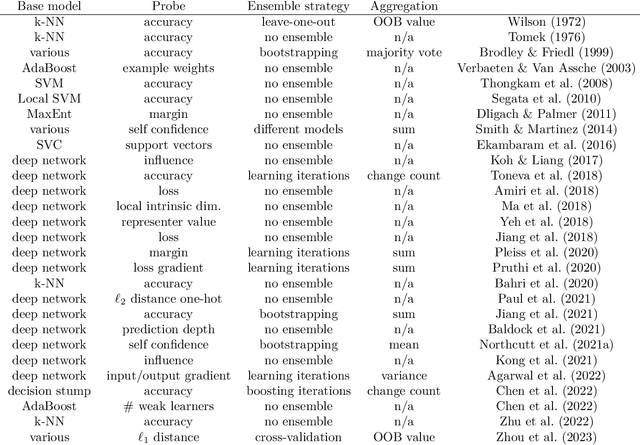
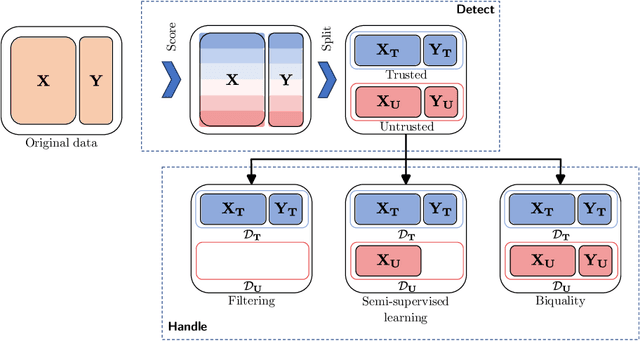
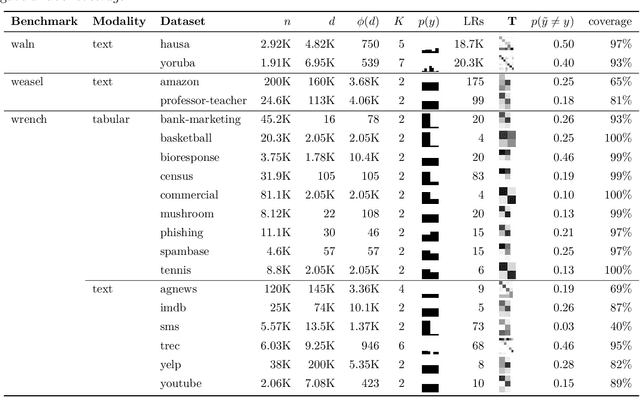
Mislabeled examples are ubiquitous in real-world machine learning datasets, advocating the development of techniques for automatic detection. We show that most mislabeled detection methods can be viewed as probing trained machine learning models using a few core principles. We formalize a modular framework that encompasses these methods, parameterized by only 4 building blocks, as well as a Python library that demonstrates that these principles can actually be implemented. The focus is on classifier-agnostic concepts, with an emphasis on adapting methods developed for deep learning models to non-deep classifiers for tabular data. We benchmark existing methods on (artificial) Completely At Random (NCAR) as well as (realistic) Not At Random (NNAR) labeling noise from a variety of tasks with imperfect labeling rules. This benchmark provides new insights as well as limitations of existing methods in this setup.

DEMAU: Decompose, Explore, Model and Analyse Uncertainties

Recent research in machine learning has given rise to a flourishing literature on the quantification and decomposition of model uncertainty. This information can be very useful during interactions with the learner, such as in active learning or adaptive learning, and especially in uncertainty sampling. To allow a simple representation of these total, epistemic (reducible) and aleatoric (irreducible) uncertainties, we offer DEMAU, an open-source educational, exploratory and analytical tool allowing to visualize and explore several types of uncertainty for classification models in machine learning.

ml_edm package: a Python toolkit for Machine Learning based Early Decision Making

\texttt{ml\_edm} is a Python 3 library, designed for early decision making of any learning tasks involving temporal/sequential data. The package is also modular, providing researchers an easy way to implement their own triggering strategy for classification, regression or any machine learning task. As of now, many Early Classification of Time Series (ECTS) state-of-the-art algorithms, are efficiently implemented in the library leveraging parallel computation. The syntax follows the one introduce in \texttt{scikit-learn}, making estimators and pipelines compatible with \texttt{ml\_edm}. This software is distributed over the BSD-3-Clause license, source code can be found at \url{https://github.com/ML-EDM/ml_edm}.

Early Classification of Time Series: Taxonomy and Benchmark

In many situations, the measurements of a studied phenomenon are provided sequentially, and the prediction of its class needs to be made as early as possible so as not to incur too high a time penalty, but not too early and risk paying the cost of misclassification. This problem has been particularly studied in the case of time series, and is known as Early Classification of Time Series (ECTS). Although it has been the subject of a growing body of literature, there is still a lack of a systematic, shared evaluation protocol to compare the relative merits of the various existing methods. This document begins by situating these methods within a principle-based taxonomy. It defines dimensions for organizing their evaluation, and then reports the results of a very extensive set of experiments along these dimensions involving nine state-of-the art ECTS algorithms. In addition, these and other experiments can be carried out using an open-source library in which most of the existing ECTS algorithms have been implemented (see \url{https://github.com/ML-EDM/ml_edm}).