A new Input Convex Neural Network with application to options pricing

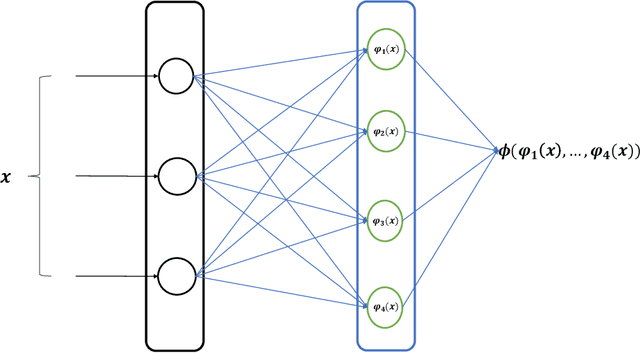
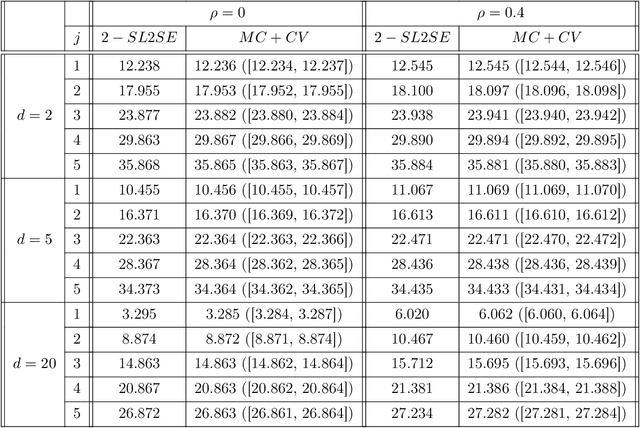
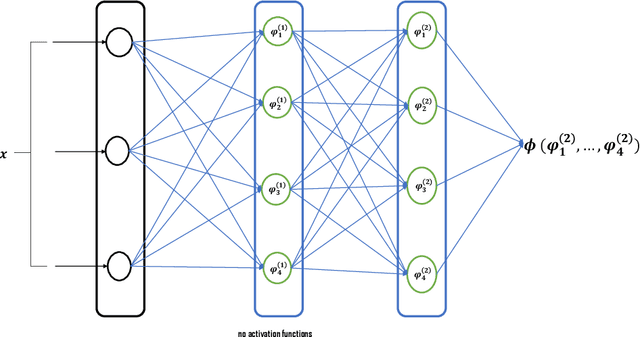
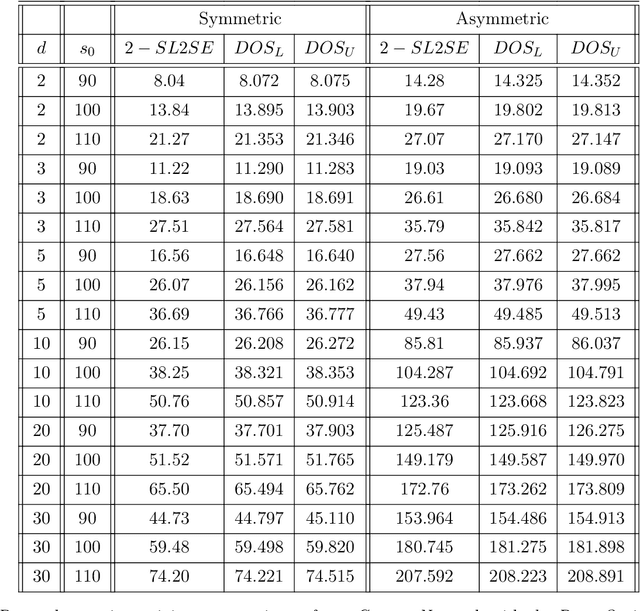
We introduce a new class of neural networks designed to be convex functions of their inputs, leveraging the principle that any convex function can be represented as the supremum of the affine functions it dominates. These neural networks, inherently convex with respect to their inputs, are particularly well-suited for approximating the prices of options with convex payoffs. We detail the architecture of this, and establish theoretical convergence bounds that validate its approximation capabilities. We also introduce a \emph{scrambling} phase to improve the training of these networks. Finally, we demonstrate numerically the effectiveness of these networks in estimating prices for three types of options with convex payoffs: Basket, Bermudan, and Swing options.

Deep multitask neural networks for solving some stochastic optimal control problems

Most existing neural network-based approaches for solving stochastic optimal control problems using the associated backward dynamic programming principle rely on the ability to simulate the underlying state variables. However, in some problems, this simulation is infeasible, leading to the discretization of state variable space and the need to train one neural network for each data point. This approach becomes computationally inefficient when dealing with large state variable spaces. In this paper, we consider a class of this type of stochastic optimal control problems and introduce an effective solution employing multitask neural networks. To train our multitask neural network, we introduce a novel scheme that dynamically balances the learning across tasks. Through numerical experiments on real-world derivatives pricing problems, we prove that our method outperforms state-of-the-art approaches.