A new Input Convex Neural Network with application to options pricing

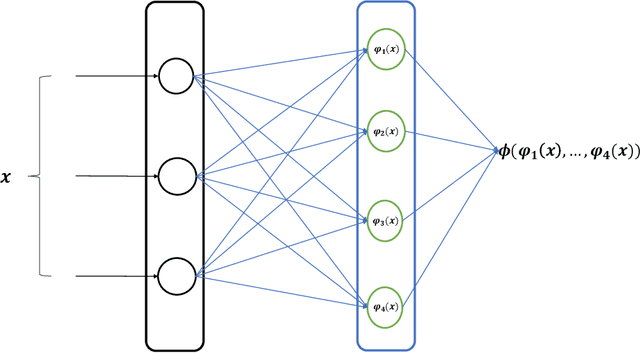
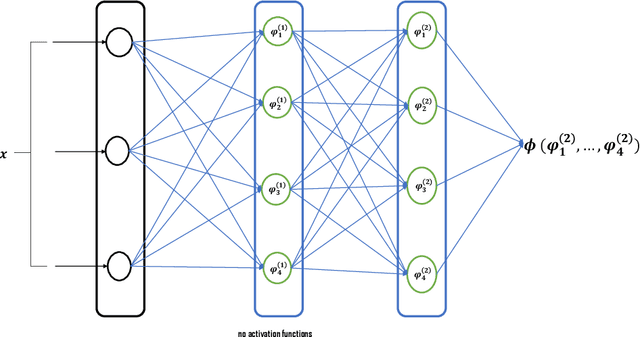
We introduce a new class of neural networks designed to be convex functions of their inputs, leveraging the principle that any convex function can be represented as the supremum of the affine functions it dominates. These neural networks, inherently convex with respect to their inputs, are particularly well-suited for approximating the prices of options with convex payoffs. We detail the architecture of this, and establish theoretical convergence bounds that validate its approximation capabilities. We also introduce a \emph{scrambling} phase to improve the training of these networks. Finally, we demonstrate numerically the effectiveness of these networks in estimating prices for three types of options with convex payoffs: Basket, Bermudan, and Swing options.

Policy Gradient Optimal Correlation Search for Variance Reduction in Monte Carlo simulation and Maximum Optimal Transport

We propose a new algorithm for variance reduction when estimating $f(X_T)$ where $X$ is the solution to some stochastic differential equation and $f$ is a test function. The new estimator is $(f(X^1_T) + f(X^2_T))/2$, where $X^1$ and $X^2$ have same marginal law as $X$ but are pathwise correlated so that to reduce the variance. The optimal correlation function $\rho$ is approximated by a deep neural network and is calibrated along the trajectories of $(X^1, X^2)$ by policy gradient and reinforcement learning techniques. Finding an optimal coupling given marginal laws has links with maximum optimal transport.

Performance of a Markovian neural network versus dynamic programming on a fishing control problem

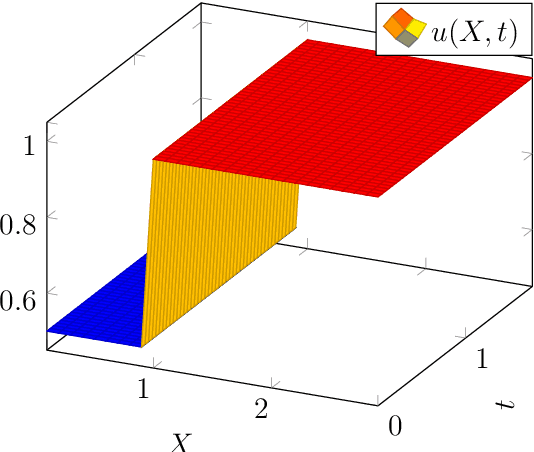
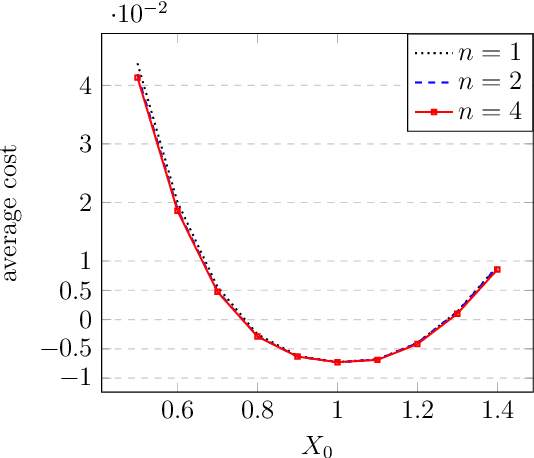
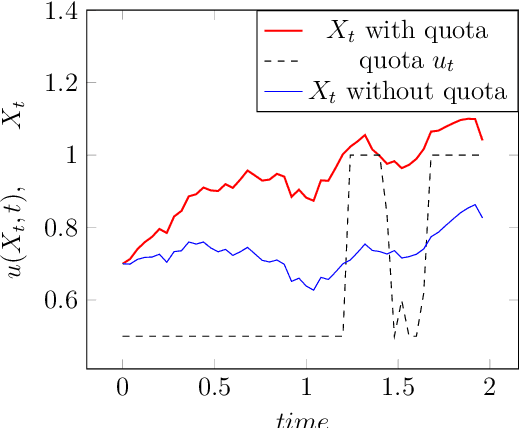
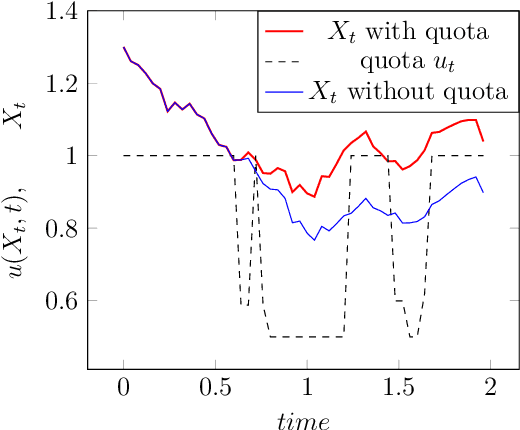
Fishing quotas are unpleasant but efficient to control the productivity of a fishing site. A popular model has a stochastic differential equation for the biomass on which a stochastic dynamic programming or a Hamilton-Jacobi-Bellman algorithm can be used to find the stochastic control -- the fishing quota. We compare the solutions obtained by dynamic programming against those obtained with a neural network which preserves the Markov property of the solution. The method is extended to a similar multi species model to check its robustness in high dimension.