On Forgetting and Stability of Score-based Generative models

Understanding the stability and long-time behavior of generative models is a fundamental problem in modern machine learning. This paper provides quantitative bounds on the sampling error of score-based generative models by leveraging stability and forgetting properties of the Markov chain associated with the reverse-time dynamics. Under weak assumptions, we provide the two structural properties to ensure the propagation of initialization and discretization errors of the backward process: a Lyapunov drift condition and a Doeblin-type minorization condition. A practical consequence is quantitative stability of the sampling procedure, as the reverse diffusion dynamics induces a contraction mechanism along the sampling trajectory. Our results clarify the role of stochastic dynamics in score-based models and provide a principled framework for analyzing propagation of errors in such approaches.

An analysis of the noise schedule for score-based generative models

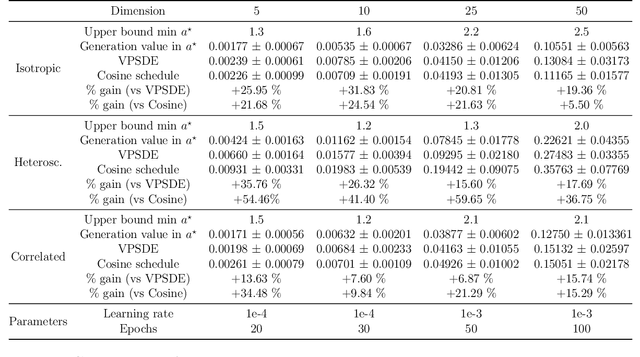
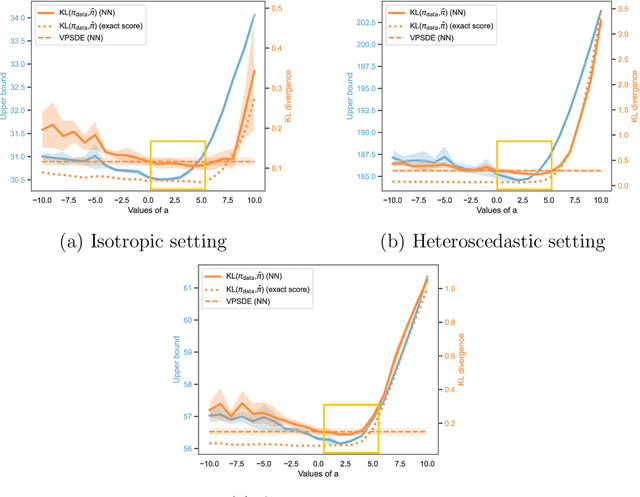
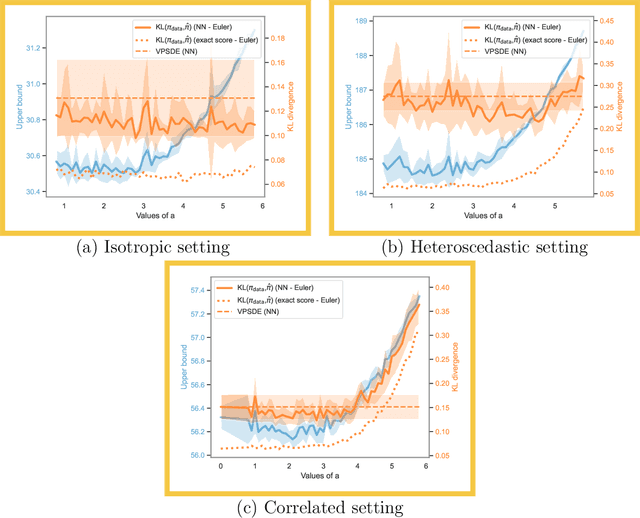
Score-based generative models (SGMs) aim at estimating a target data distribution by learning score functions using only noise-perturbed samples from the target. Recent literature has focused extensively on assessing the error between the target and estimated distributions, gauging the generative quality through the Kullback-Leibler (KL) divergence and Wasserstein distances. All existing results have been obtained so far for time-homogeneous speed of the noise schedule. Under mild assumptions on the data distribution, we establish an upper bound for the KL divergence between the target and the estimated distributions, explicitly depending on any time-dependent noise schedule. Assuming that the score is Lipschitz continuous, we provide an improved error bound in Wasserstein distance, taking advantage of favourable underlying contraction mechanisms. We also propose an algorithm to automatically tune the noise schedule using the proposed upper bound. We illustrate empirically the performance of the noise schedule optimization in comparison to standard choices in the literature.