Theoretical Convergence Guarantees for Variational Autoencoders

Variational Autoencoders (VAE) are popular generative models used to sample from complex data distributions. Despite their empirical success in various machine learning tasks, significant gaps remain in understanding their theoretical properties, particularly regarding convergence guarantees. This paper aims to bridge that gap by providing non-asymptotic convergence guarantees for VAE trained using both Stochastic Gradient Descent and Adam algorithms.We derive a convergence rate of $\mathcal{O}(\log n / \sqrt{n})$, where $n$ is the number of iterations of the optimization algorithm, with explicit dependencies on the batch size, the number of variational samples, and other key hyperparameters. Our theoretical analysis applies to both Linear VAE and Deep Gaussian VAE, as well as several VAE variants, including $\beta$-VAE and IWAE. Additionally, we empirically illustrate the impact of hyperparameters on convergence, offering new insights into the theoretical understanding of VAE training.

Tree-based variational inference for Poisson log-normal models

When studying ecosystems, hierarchical trees are often used to organize entities based on proximity criteria, such as the taxonomy in microbiology, social classes in geography, or product types in retail businesses, offering valuable insights into entity relationships. Despite their significance, current count-data models do not leverage this structured information. In particular, the widely used Poisson log-normal (PLN) model, known for its ability to model interactions between entities from count data, lacks the possibility to incorporate such hierarchical tree structures, limiting its applicability in domains characterized by such complexities. To address this matter, we introduce the PLN-Tree model as an extension of the PLN model, specifically designed for modeling hierarchical count data. By integrating structured variational inference techniques, we propose an adapted training procedure and establish identifiability results, enhancisng both theoretical foundations and practical interpretability. Additionally, we extend our framework to classification tasks as a preprocessing pipeline, showcasing its versatility. Experimental evaluations on synthetic datasets as well as real-world microbiome data demonstrate the superior performance of the PLN-Tree model in capturing hierarchical dependencies and providing valuable insights into complex data structures, showing the practical interest of knowledge graphs like the taxonomy in ecosystems modeling.

Variational quantization for state space models

Forecasting tasks using large datasets gathering thousands of heterogeneous time series is a crucial statistical problem in numerous sectors. The main challenge is to model a rich variety of time series, leverage any available external signals and provide sharp predictions with statistical guarantees. In this work, we propose a new forecasting model that combines discrete state space hidden Markov models with recent neural network architectures and training procedures inspired by vector quantized variational autoencoders. We introduce a variational discrete posterior distribution of the latent states given the observations and a two-stage training procedure to alternatively train the parameters of the latent states and of the emission distributions. By learning a collection of emission laws and temporarily activating them depending on the hidden process dynamics, the proposed method allows to explore large datasets and leverage available external signals. We assess the performance of the proposed method using several datasets and show that it outperforms other state-of-the-art solutions.

Diffusion posterior sampling for simulation-based inference in tall data settings

Determining which parameters of a non-linear model could best describe a set of experimental data is a fundamental problem in science and it has gained much traction lately with the rise of complex large-scale simulators (a.k.a. black-box simulators). The likelihood of such models is typically intractable, which is why classical MCMC methods can not be used. Simulation-based inference (SBI) stands out in this context by only requiring a dataset of simulations to train deep generative models capable of approximating the posterior distribution that relates input parameters to a given observation. In this work, we consider a tall data extension in which multiple observations are available and one wishes to leverage their shared information to better infer the parameters of the model. The method we propose is built upon recent developments from the flourishing score-based diffusion literature and allows us to estimate the tall data posterior distribution simply using information from the score network trained on individual observations. We compare our method to recently proposed competing approaches on various numerical experiments and demonstrate its superiority in terms of numerical stability and computational cost.

An analysis of the noise schedule for score-based generative models

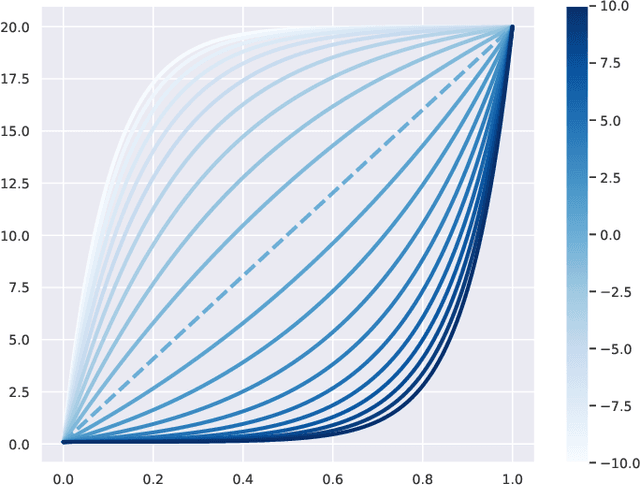
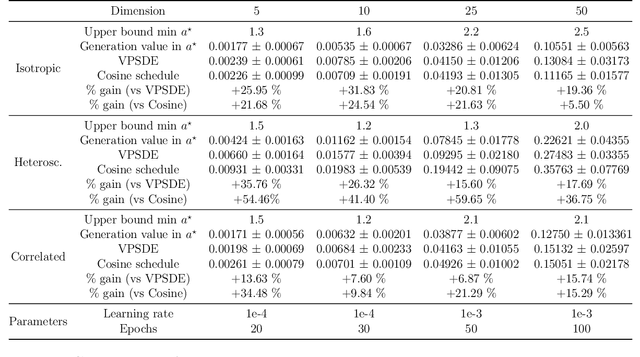
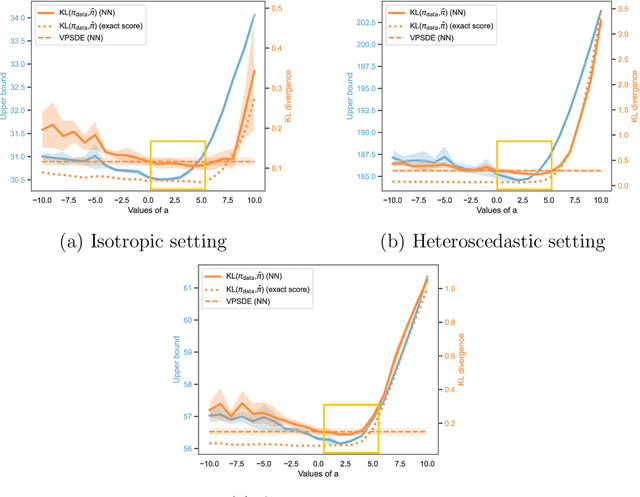
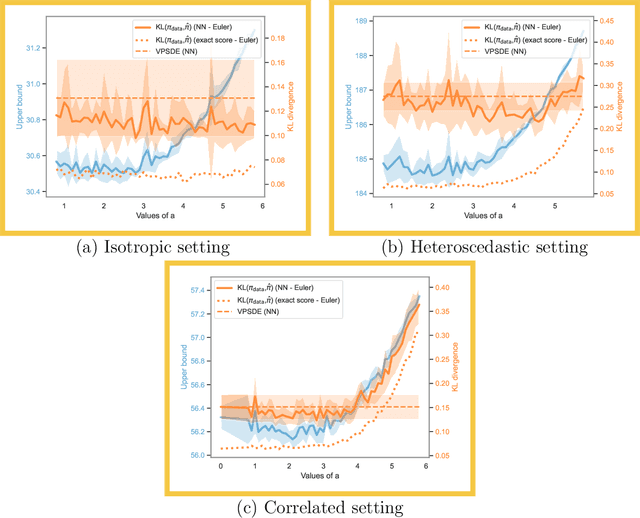
Score-based generative models (SGMs) aim at estimating a target data distribution by learning score functions using only noise-perturbed samples from the target. Recent literature has focused extensively on assessing the error between the target and estimated distributions, gauging the generative quality through the Kullback-Leibler (KL) divergence and Wasserstein distances. All existing results have been obtained so far for time-homogeneous speed of the noise schedule. Under mild assumptions on the data distribution, we establish an upper bound for the KL divergence between the target and the estimated distributions, explicitly depending on any time-dependent noise schedule. Assuming that the score is Lipschitz continuous, we provide an improved error bound in Wasserstein distance, taking advantage of favourable underlying contraction mechanisms. We also propose an algorithm to automatically tune the noise schedule using the proposed upper bound. We illustrate empirically the performance of the noise schedule optimization in comparison to standard choices in the literature.

Importance sampling for online variational learning

This article addresses online variational estimation in state-space models. We focus on learning the smoothing distribution, i.e. the joint distribution of the latent states given the observations, using a variational approach together with Monte Carlo importance sampling. We propose an efficient algorithm for computing the gradient of the evidence lower bound (ELBO) in the context of streaming data, where observations arrive sequentially. Our contributions include a computationally efficient online ELBO estimator, demonstrated performance in offline and true online settings, and adaptability for computing general expectations under joint smoothing distributions.

Non-asymptotic Analysis of Biased Adaptive Stochastic Approximation

Stochastic Gradient Descent (SGD) with adaptive steps is now widely used for training deep neural networks. Most theoretical results assume access to unbiased gradient estimators, which is not the case in several recent deep learning and reinforcement learning applications that use Monte Carlo methods. This paper provides a comprehensive non-asymptotic analysis of SGD with biased gradients and adaptive steps for convex and non-convex smooth functions. Our study incorporates time-dependent bias and emphasizes the importance of controlling the bias and Mean Squared Error (MSE) of the gradient estimator. In particular, we establish that Adagrad and RMSProp with biased gradients converge to critical points for smooth non-convex functions at a rate similar to existing results in the literature for the unbiased case. Finally, we provide experimental results using Variational Autoenconders (VAE) that illustrate our convergence results and show how the effect of bias can be reduced by appropriate hyperparameter tuning.

Variational excess risk bound for general state space models

In this paper, we consider variational autoencoders (VAE) for general state space models. We consider a backward factorization of the variational distributions to analyze the excess risk associated with VAE. Such backward factorizations were recently proposed to perform online variational learning and to obtain upper bounds on the variational estimation error. When independent trajectories of sequences are observed and under strong mixing assumptions on the state space model and on the variational distribution, we provide an oracle inequality explicit in the number of samples and in the length of the observation sequences. We then derive consequences of this theoretical result. In particular, when the data distribution is given by a state space model, we provide an upper bound for the Kullback-Leibler divergence between the data distribution and its estimator and between the variational posterior and the estimated state space posterior distributions.Under classical assumptions, we prove that our results can be applied to Gaussian backward kernels built with dense and recurrent neural networks.

Monte Carlo guided Diffusion for Bayesian linear inverse problems

Ill-posed linear inverse problems that combine knowledge of the forward measurement model with prior models arise frequently in various applications, from computational photography to medical imaging. Recent research has focused on solving these problems with score-based generative models (SGMs) that produce perceptually plausible images, especially in inpainting problems. In this study, we exploit the particular structure of the prior defined in the SGM to formulate recovery in a Bayesian framework as a Feynman--Kac model adapted from the forward diffusion model used to construct score-based diffusion. To solve this Feynman--Kac problem, we propose the use of Sequential Monte Carlo methods. The proposed algorithm, MCGdiff, is shown to be theoretically grounded and we provide numerical simulations showing that it outperforms competing baselines when dealing with ill-posed inverse problems.

Last layer state space model for representation learning and uncertainty quantification

As sequential neural architectures become deeper and more complex, uncertainty estimation is more and more challenging. Efforts in quantifying uncertainty often rely on specific training procedures, and bear additional computational costs due to the dimensionality of such models. In this paper, we propose to decompose a classification or regression task in two steps: a representation learning stage to learn low-dimensional states, and a state space model for uncertainty estimation. This approach allows to separate representation learning and design of generative models. We demonstrate how predictive distributions can be estimated on top of an existing and trained neural network, by adding a state space-based last layer whose parameters are estimated with Sequential Monte Carlo methods. We apply our proposed methodology to the hourly estimation of Electricity Transformer Oil temperature, a publicly benchmarked dataset. Our model accounts for the noisy data structure, due to unknown or unavailable variables, and is able to provide confidence intervals on predictions.