Categorical Reparameterization with Denoising Diffusion models

Gradient-based optimization with categorical variables typically relies on score-function estimators, which are unbiased but noisy, or on continuous relaxations that replace the discrete distribution with a smooth surrogate admitting a pathwise (reparameterized) gradient, at the cost of optimizing a biased, temperature-dependent objective. In this paper, we extend this family of relaxations by introducing a diffusion-based soft reparameterization for categorical distributions. For these distributions, the denoiser under a Gaussian noising process admits a closed form and can be computed efficiently, yielding a training-free diffusion sampler through which we can backpropagate. Our experiments show that the proposed reparameterization trick yields competitive or improved optimization performance on various benchmarks.

Efficient Zero-Shot Inpainting with Decoupled Diffusion Guidance

Diffusion models have emerged as powerful priors for image editing tasks such as inpainting and local modification, where the objective is to generate realistic content that remains consistent with observed regions. In particular, zero-shot approaches that leverage a pretrained diffusion model, without any retraining, have been shown to achieve highly effective reconstructions. However, state-of-the-art zero-shot methods typically rely on a sequence of surrogate likelihood functions, whose scores are used as proxies for the ideal score. This procedure however requires vector-Jacobian products through the denoiser at every reverse step, introducing significant memory and runtime overhead. To address this issue, we propose a new likelihood surrogate that yields simple and efficient to sample Gaussian posterior transitions, sidestepping the backpropagation through the denoiser network. Our extensive experiments show that our method achieves strong observation consistency compared with fine-tuned baselines and produces coherent, high-quality reconstructions, all while significantly reducing inference cost. Code is available at https://github.com/YazidJanati/ding.

Controllable protein design through Feynman-Kac steering

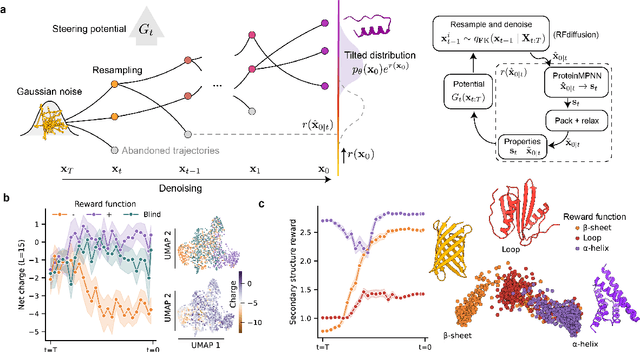
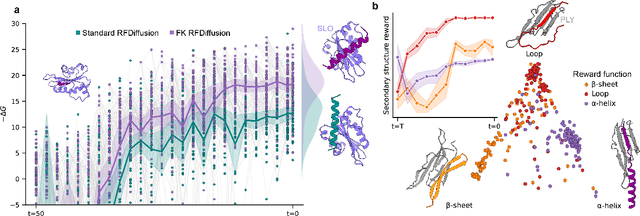
Diffusion-based models have recently enabled the generation of realistic and diverse protein structures, yet they remain limited in their ability to steer outcomes toward specific functional or biochemical objectives, such as binding affinity or sequence composition. Here we extend the Feynman-Kac (FK) steering framework, an inference-time control approach, to diffusion-based protein design. By coupling FK steering with structure generation, the method guides sampling toward desirable structural or energetic features while maintaining the diversity of the underlying diffusion process. To enable simultaneous generation of both sequence and structure properties, rewards are computed on models refined through ProteinMPNN and all-atom relaxation. Applied to binder design, FK steering consistently improves predicted interface energetics across diverse targets with minimal computational overhead. More broadly, this work demonstrates that inference-time FK control generalizes diffusion-based protein design to arbitrary, non-differentiable, and reward-agnostic objectives, providing a unified and model-independent framework for guided molecular generation.

Briding Diffusion Posterior Sampling and Monte Carlo methods: a survey

Diffusion models enable the synthesis of highly accurate samples from complex distributions and have become foundational in generative modeling. Recently, they have demonstrated significant potential for solving Bayesian inverse problems by serving as priors. This review offers a comprehensive overview of current methods that leverage \emph{pre-trained} diffusion models alongside Monte Carlo methods to address Bayesian inverse problems without requiring additional training. We show that these methods primarily employ a \emph{twisting} mechanism for the intermediate distributions within the diffusion process, guiding the simulations toward the posterior distribution. We describe how various Monte Carlo methods are then used to aid in sampling from these twisted distributions.

Conditional Diffusion Models with Classifier-Free Gibbs-like Guidance

Classifier-Free Guidance (CFG) is a widely used technique for improving conditional diffusion models by linearly combining the outputs of conditional and unconditional denoisers. While CFG enhances visual quality and improves alignment with prompts, it often reduces sample diversity, leading to a challenging trade-off between quality and diversity. To address this issue, we make two key contributions. First, CFG generally does not correspond to a well-defined denoising diffusion model (DDM). In particular, contrary to common intuition, CFG does not yield samples from the target distribution associated with the limiting CFG score as the noise level approaches zero -- where the data distribution is tilted by a power $w \gt 1$ of the conditional distribution. We identify the missing component: a R\'enyi divergence term that acts as a repulsive force and is required to correct CFG and render it consistent with a proper DDM. Our analysis shows that this correction term vanishes in the low-noise limit. Second, motivated by this insight, we propose a Gibbs-like sampling procedure to draw samples from the desired tilted distribution. This method starts with an initial sample from the conditional diffusion model without CFG and iteratively refines it, preserving diversity while progressively enhancing sample quality. We evaluate our approach on both image and text-to-audio generation tasks, demonstrating substantial improvements over CFG across all considered metrics. The code is available at https://github.com/yazidjanati/cfgig

A Mixture-Based Framework for Guiding Diffusion Models

Denoising diffusion models have driven significant progress in the field of Bayesian inverse problems. Recent approaches use pre-trained diffusion models as priors to solve a wide range of such problems, only leveraging inference-time compute and thereby eliminating the need to retrain task-specific models on the same dataset. To approximate the posterior of a Bayesian inverse problem, a diffusion model samples from a sequence of intermediate posterior distributions, each with an intractable likelihood function. This work proposes a novel mixture approximation of these intermediate distributions. Since direct gradient-based sampling of these mixtures is infeasible due to intractable terms, we propose a practical method based on Gibbs sampling. We validate our approach through extensive experiments on image inverse problems, utilizing both pixel- and latent-space diffusion priors, as well as on source separation with an audio diffusion model. The code is available at https://www.github.com/badr-moufad/mgdm

Recursive Learning of Asymptotic Variational Objectives

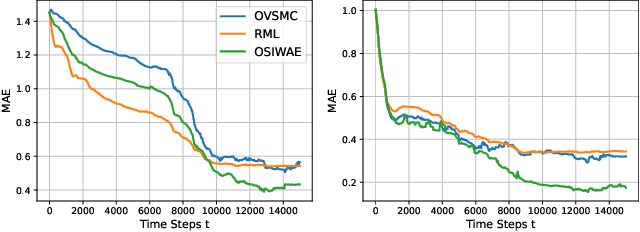
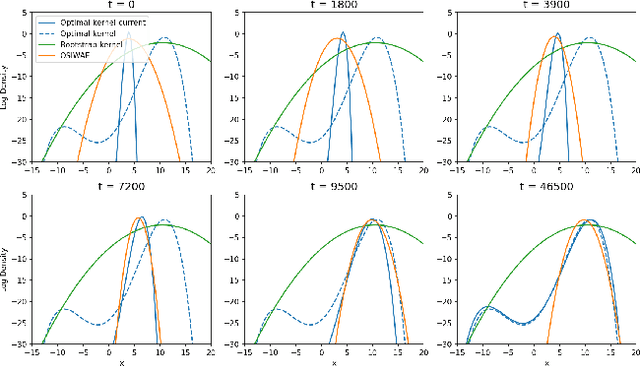
General state-space models (SSMs) are widely used in statistical machine learning and are among the most classical generative models for sequential time-series data. SSMs, comprising latent Markovian states, can be subjected to variational inference (VI), but standard VI methods like the importance-weighted autoencoder (IWAE) lack functionality for streaming data. To enable online VI in SSMs when the observations are received in real time, we propose maximising an IWAE-type variational lower bound on the asymptotic contrast function, rather than the standard IWAE ELBO, using stochastic approximation. Unlike the recursive maximum likelihood method, which directly maximises the asymptotic contrast, our approach, called online sequential IWAE (OSIWAE), allows for online learning of both model parameters and a Markovian recognition model for inferring latent states. By approximating filter state posteriors and their derivatives using sequential Monte Carlo (SMC) methods, we create a particle-based framework for online VI in SSMs. This approach is more theoretically well-founded than recently proposed online variational SMC methods. We provide rigorous theoretical results on the learning objective and a numerical study demonstrating the method's efficiency in learning model parameters and particle proposal kernels.

Variational Diffusion Posterior Sampling with Midpoint Guidance

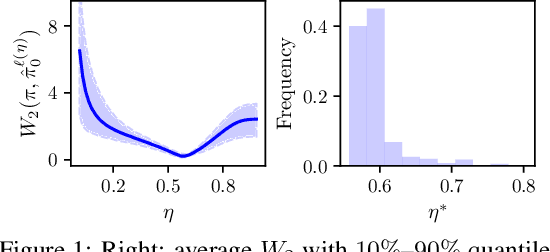
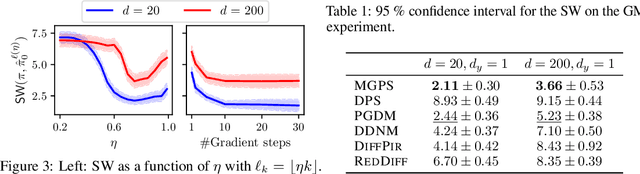
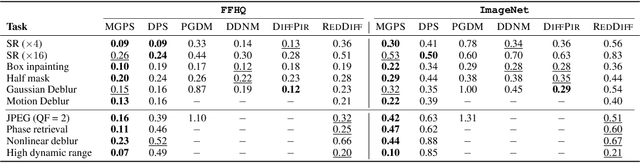
Diffusion models have recently shown considerable potential in solving Bayesian inverse problems when used as priors. However, sampling from the resulting denoising posterior distributions remains a challenge as it involves intractable terms. To tackle this issue, state-of-the-art approaches formulate the problem as that of sampling from a surrogate diffusion model targeting the posterior and decompose its scores into two terms: the prior score and an intractable guidance term. While the former is replaced by the pre-trained score of the considered diffusion model, the guidance term has to be estimated. In this paper, we propose a novel approach that utilises a decomposition of the transitions which, in contrast to previous methods, allows a trade-off between the complexity of the intractable guidance term and that of the prior transitions. We validate the proposed approach through extensive experiments on linear and nonlinear inverse problems, including challenging cases with latent diffusion models as priors, and demonstrate its effectiveness in reconstructing electrocardiogram (ECG) from partial measurements for accurate cardiac diagnosis.

Divide-and-Conquer Posterior Sampling for Denoising Diffusion Priors

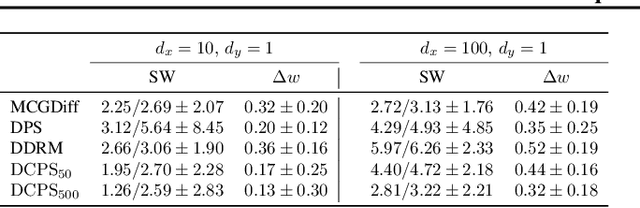
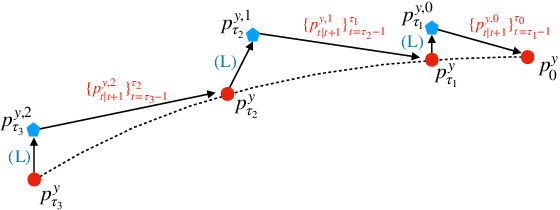
Interest in the use of Denoising Diffusion Models (DDM) as priors for solving inverse Bayesian problems has recently increased significantly. However, sampling from the resulting posterior distribution poses a challenge. To solve this problem, previous works have proposed approximations to bias the drift term of the diffusion. In this work, we take a different approach and utilize the specific structure of the DDM prior to define a set of intermediate and simpler posterior sampling problems, resulting in a lower approximation error compared to previous methods. We empirically demonstrate the reconstruction capability of our method for general linear inverse problems using synthetic examples and various image restoration tasks.

Importance sampling for online variational learning

This article addresses online variational estimation in state-space models. We focus on learning the smoothing distribution, i.e. the joint distribution of the latent states given the observations, using a variational approach together with Monte Carlo importance sampling. We propose an efficient algorithm for computing the gradient of the evidence lower bound (ELBO) in the context of streaming data, where observations arrive sequentially. Our contributions include a computationally efficient online ELBO estimator, demonstrated performance in offline and true online settings, and adaptability for computing general expectations under joint smoothing distributions.