Entropic Mirror Monte Carlo

Importance sampling is a Monte Carlo method which designs estimators of expectations under a target distribution using weighted samples from a proposal distribution. When the target distribution is complex, such as multimodal distributions in highdimensional spaces, the efficiency of importance sampling critically depends on the choice of the proposal distribution. In this paper, we propose a novel adaptive scheme for the construction of efficient proposal distributions. Our algorithm promotes efficient exploration of the target distribution by combining global sampling mechanisms with a delayed weighting procedure. The proposed weighting mechanism plays a key role by enabling rapid resampling in regions where the proposal distribution is poorly adapted to the target. Our sampling algorithm is shown to be geometrically convergent under mild assumptions and is illustrated through various numerical experiments.

Categorical Reparameterization with Denoising Diffusion models

Gradient-based optimization with categorical variables typically relies on score-function estimators, which are unbiased but noisy, or on continuous relaxations that replace the discrete distribution with a smooth surrogate admitting a pathwise (reparameterized) gradient, at the cost of optimizing a biased, temperature-dependent objective. In this paper, we extend this family of relaxations by introducing a diffusion-based soft reparameterization for categorical distributions. For these distributions, the denoiser under a Gaussian noising process admits a closed form and can be computed efficiently, yielding a training-free diffusion sampler through which we can backpropagate. Our experiments show that the proposed reparameterization trick yields competitive or improved optimization performance on various benchmarks.

Efficient Zero-Shot Inpainting with Decoupled Diffusion Guidance

Diffusion models have emerged as powerful priors for image editing tasks such as inpainting and local modification, where the objective is to generate realistic content that remains consistent with observed regions. In particular, zero-shot approaches that leverage a pretrained diffusion model, without any retraining, have been shown to achieve highly effective reconstructions. However, state-of-the-art zero-shot methods typically rely on a sequence of surrogate likelihood functions, whose scores are used as proxies for the ideal score. This procedure however requires vector-Jacobian products through the denoiser at every reverse step, introducing significant memory and runtime overhead. To address this issue, we propose a new likelihood surrogate that yields simple and efficient to sample Gaussian posterior transitions, sidestepping the backpropagation through the denoiser network. Our extensive experiments show that our method achieves strong observation consistency compared with fine-tuned baselines and produces coherent, high-quality reconstructions, all while significantly reducing inference cost. Code is available at https://github.com/YazidJanati/ding.

Briding Diffusion Posterior Sampling and Monte Carlo methods: a survey

Diffusion models enable the synthesis of highly accurate samples from complex distributions and have become foundational in generative modeling. Recently, they have demonstrated significant potential for solving Bayesian inverse problems by serving as priors. This review offers a comprehensive overview of current methods that leverage \emph{pre-trained} diffusion models alongside Monte Carlo methods to address Bayesian inverse problems without requiring additional training. We show that these methods primarily employ a \emph{twisting} mechanism for the intermediate distributions within the diffusion process, guiding the simulations toward the posterior distribution. We describe how various Monte Carlo methods are then used to aid in sampling from these twisted distributions.

Conditional Diffusion Models with Classifier-Free Gibbs-like Guidance

Classifier-Free Guidance (CFG) is a widely used technique for improving conditional diffusion models by linearly combining the outputs of conditional and unconditional denoisers. While CFG enhances visual quality and improves alignment with prompts, it often reduces sample diversity, leading to a challenging trade-off between quality and diversity. To address this issue, we make two key contributions. First, CFG generally does not correspond to a well-defined denoising diffusion model (DDM). In particular, contrary to common intuition, CFG does not yield samples from the target distribution associated with the limiting CFG score as the noise level approaches zero -- where the data distribution is tilted by a power $w \gt 1$ of the conditional distribution. We identify the missing component: a R\'enyi divergence term that acts as a repulsive force and is required to correct CFG and render it consistent with a proper DDM. Our analysis shows that this correction term vanishes in the low-noise limit. Second, motivated by this insight, we propose a Gibbs-like sampling procedure to draw samples from the desired tilted distribution. This method starts with an initial sample from the conditional diffusion model without CFG and iteratively refines it, preserving diversity while progressively enhancing sample quality. We evaluate our approach on both image and text-to-audio generation tasks, demonstrating substantial improvements over CFG across all considered metrics. The code is available at https://github.com/yazidjanati/cfgig

A Mixture-Based Framework for Guiding Diffusion Models

Denoising diffusion models have driven significant progress in the field of Bayesian inverse problems. Recent approaches use pre-trained diffusion models as priors to solve a wide range of such problems, only leveraging inference-time compute and thereby eliminating the need to retrain task-specific models on the same dataset. To approximate the posterior of a Bayesian inverse problem, a diffusion model samples from a sequence of intermediate posterior distributions, each with an intractable likelihood function. This work proposes a novel mixture approximation of these intermediate distributions. Since direct gradient-based sampling of these mixtures is infeasible due to intractable terms, we propose a practical method based on Gibbs sampling. We validate our approach through extensive experiments on image inverse problems, utilizing both pixel- and latent-space diffusion priors, as well as on source separation with an audio diffusion model. The code is available at https://www.github.com/badr-moufad/mgdm

Variational Diffusion Posterior Sampling with Midpoint Guidance

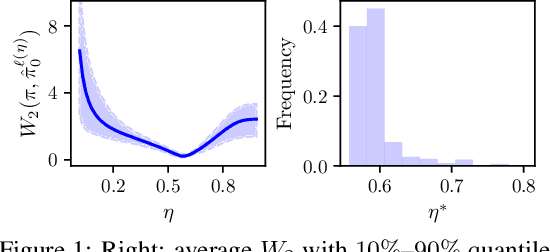
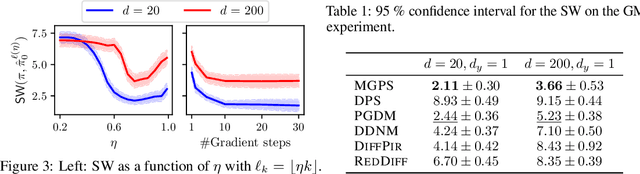
Diffusion models have recently shown considerable potential in solving Bayesian inverse problems when used as priors. However, sampling from the resulting denoising posterior distributions remains a challenge as it involves intractable terms. To tackle this issue, state-of-the-art approaches formulate the problem as that of sampling from a surrogate diffusion model targeting the posterior and decompose its scores into two terms: the prior score and an intractable guidance term. While the former is replaced by the pre-trained score of the considered diffusion model, the guidance term has to be estimated. In this paper, we propose a novel approach that utilises a decomposition of the transitions which, in contrast to previous methods, allows a trade-off between the complexity of the intractable guidance term and that of the prior transitions. We validate the proposed approach through extensive experiments on linear and nonlinear inverse problems, including challenging cases with latent diffusion models as priors, and demonstrate its effectiveness in reconstructing electrocardiogram (ECG) from partial measurements for accurate cardiac diagnosis.

Divide-and-Conquer Posterior Sampling for Denoising Diffusion Priors

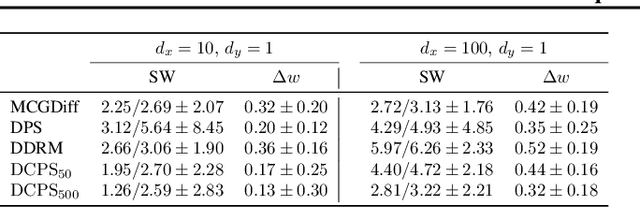
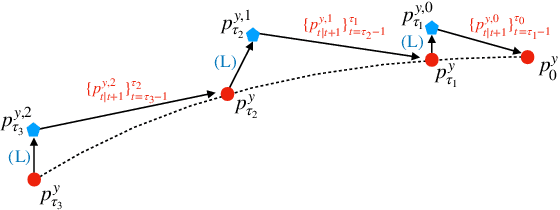
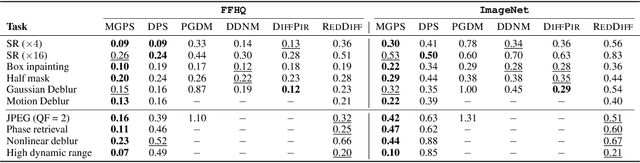
Interest in the use of Denoising Diffusion Models (DDM) as priors for solving inverse Bayesian problems has recently increased significantly. However, sampling from the resulting posterior distribution poses a challenge. To solve this problem, previous works have proposed approximations to bias the drift term of the diffusion. In this work, we take a different approach and utilize the specific structure of the DDM prior to define a set of intermediate and simpler posterior sampling problems, resulting in a lower approximation error compared to previous methods. We empirically demonstrate the reconstruction capability of our method for general linear inverse problems using synthetic examples and various image restoration tasks.

Invertible Flow Non Equilibrium sampling

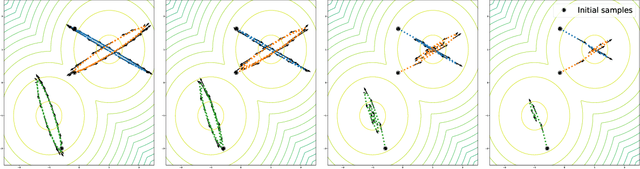
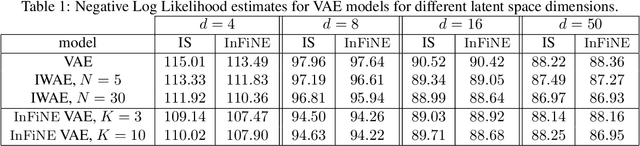
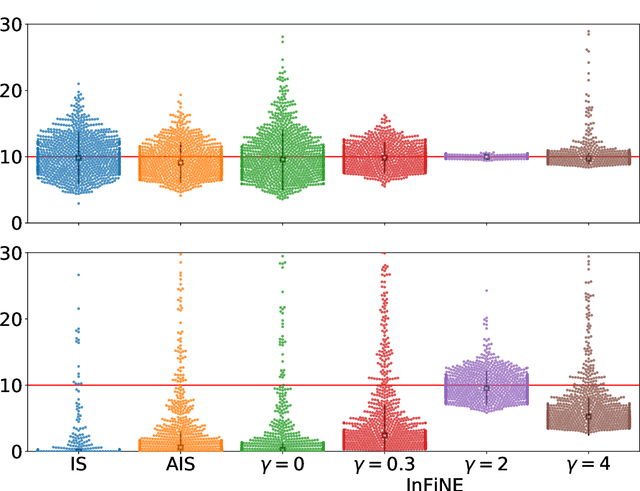
Simultaneously sampling from a complex distribution with intractable normalizing constant and approximating expectations under this distribution is a notoriously challenging problem. We introduce a novel scheme, Invertible Flow Non Equilibrium Sampling (InFine), which departs from classical Sequential Monte Carlo (SMC) and Markov chain Monte Carlo (MCMC) approaches. InFine constructs unbiased estimators of expectations and in particular of normalizing constants by combining the orbits of a deterministic transform started from random initializations.When this transform is chosen as an appropriate integrator of a conformal Hamiltonian system, these orbits are optimization paths. InFine is also naturally suited to design new MCMC sampling schemes by selecting samples on the optimization paths.Additionally, InFine can be used to construct an Evidence Lower Bound (ELBO) leading to a new class of Variational AutoEncoders (VAE).