Variational Diffusion Posterior Sampling with Midpoint Guidance

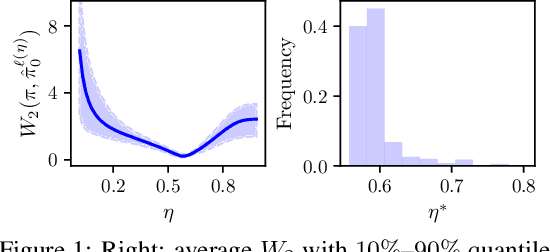
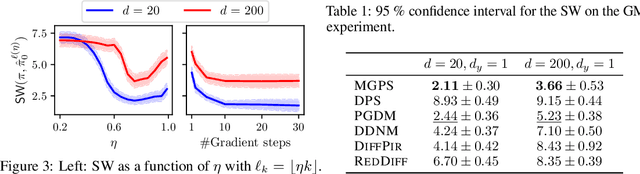
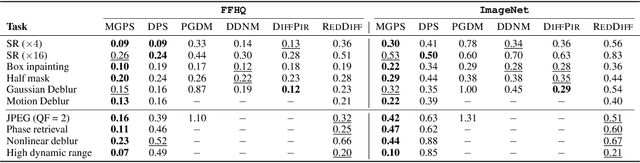
Diffusion models have recently shown considerable potential in solving Bayesian inverse problems when used as priors. However, sampling from the resulting denoising posterior distributions remains a challenge as it involves intractable terms. To tackle this issue, state-of-the-art approaches formulate the problem as that of sampling from a surrogate diffusion model targeting the posterior and decompose its scores into two terms: the prior score and an intractable guidance term. While the former is replaced by the pre-trained score of the considered diffusion model, the guidance term has to be estimated. In this paper, we propose a novel approach that utilises a decomposition of the transitions which, in contrast to previous methods, allows a trade-off between the complexity of the intractable guidance term and that of the prior transitions. We validate the proposed approach through extensive experiments on linear and nonlinear inverse problems, including challenging cases with latent diffusion models as priors, and demonstrate its effectiveness in reconstructing electrocardiogram (ECG) from partial measurements for accurate cardiac diagnosis.

Asymptotic convergence of iterative optimization algorithms

This paper introduces a general framework for iterative optimization algorithms and establishes under general assumptions that their convergence is asymptotically geometric. We also prove that under appropriate assumptions, the rate of convergence can be lower bounded. The convergence is then only geometric, and we provide the exact asymptotic convergence rate. This framework allows to deal with constrained optimization and encompasses the Expectation Maximization algorithm and the mirror descent algorithm, as well as some variants such as the alpha-Expectation Maximization or the Mirror Prox algorithm.Furthermore, we establish sufficient conditions for the convergence of the Mirror Prox algorithm, under which the method converges systematically to the unique minimizer of a convex function on a convex compact set.

Mixture weights optimisation for Alpha-Divergence Variational Inference

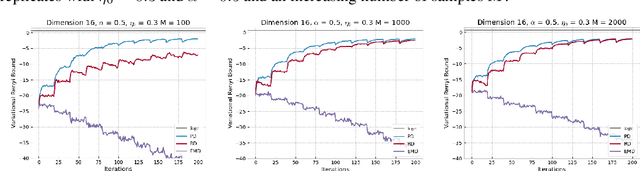
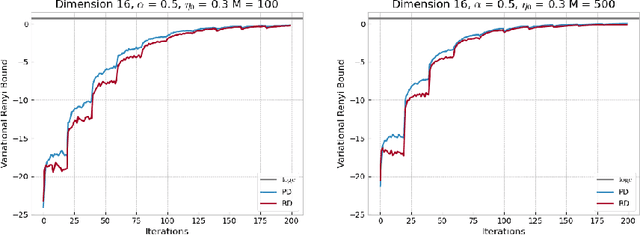
This paper focuses on $\alpha$-divergence minimisation methods for Variational Inference. More precisely, we are interested in algorithms optimising the mixture weights of any given mixture model, without any information on the underlying distribution of its mixture components parameters. The Power Descent, defined for all $\alpha \neq 1$, is one such algorithm and we establish in our work the full proof of its convergence towards the optimal mixture weights when $\alpha <1$. Since the $\alpha$-divergence recovers the widely-used forward Kullback-Leibler when $\alpha \to 1$, we then extend the Power Descent to the case $\alpha = 1$ and show that we obtain an Entropic Mirror Descent. This leads us to investigate the link between Power Descent and Entropic Mirror Descent: first-order approximations allow us to introduce the Renyi Descent, a novel algorithm for which we prove an $O(1/N)$ convergence rate. Lastly, we compare numerically the behavior of the unbiased Power Descent and of the biased Renyi Descent and we discuss the potential advantages of one algorithm over the other.

Monotonic Alpha-divergence Minimisation

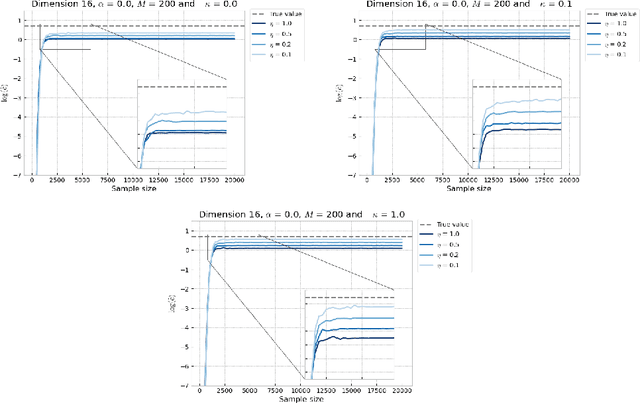
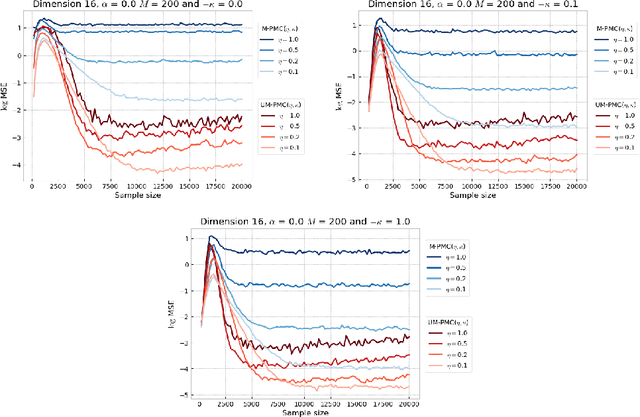
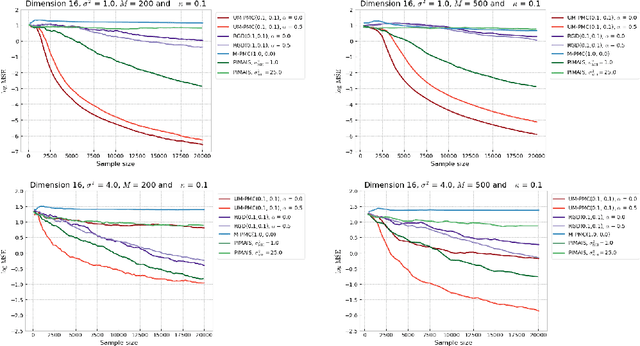
In this paper, we introduce a novel iterative algorithm which carries out $\alpha$-divergence minimisation by ensuring a systematic decrease in the $\alpha$-divergence at each step. In its most general form, our framework allows us to simultaneously optimise the weights and components parameters of a given mixture model. Notably, our approach permits to build on various methods previously proposed for $\alpha$-divergence minimisation such as gradient or power descent schemes. Furthermore, we shed a new light on an integrated Expectation Maximization algorithm. We provide empirical evidence that our methodology yields improved results, all the while illustrating the numerical benefits of having introduced some flexibility through the parameter $\alpha$ of the $\alpha$-divergence.

Online Approximate Bayesian learning

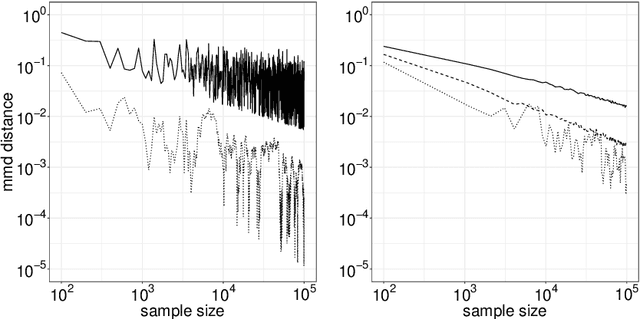
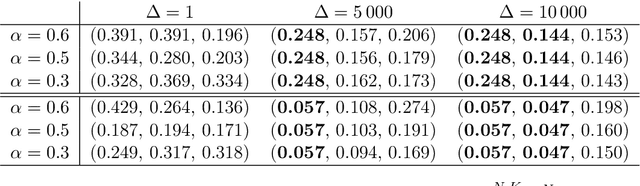
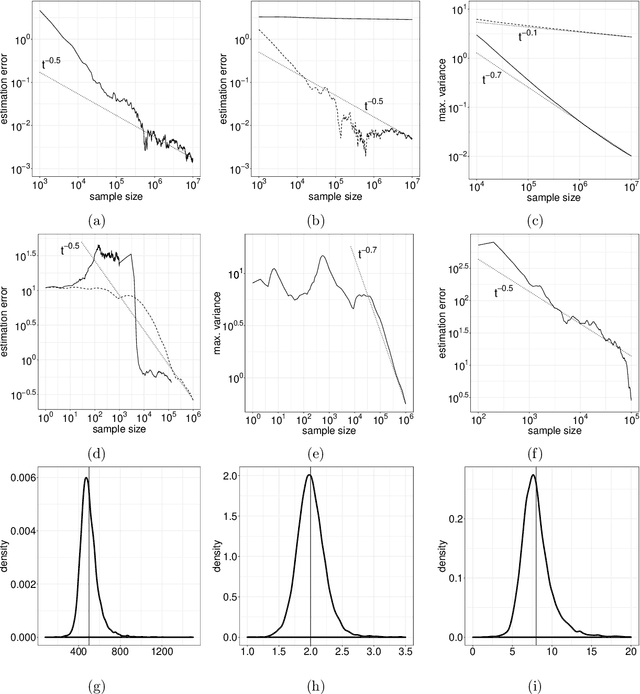
We introduce in this work a new method for online approximate Bayesian learning, whose main idea is to approximate the sequence $(\pi_t)_{t\geq 1}$ of posterior distributions by a sequence $(\tilde{\pi}_t)_{t\geq 1}$ which (i) can be estimated in an online fashion using sequential Monte Carlo methods and (ii) is shown to converge to the same distribution as the sequence $(\pi_t)_{t\geq 1}$, under weak assumptions on the statistical model at hand. In its simplest version, the proposed approach amounts to take for $(\tilde{\pi}_t)_{t\geq 1}$ the sequence of filtering distributions associated to a particular state-space model, and to approximate this sequence using a standard particle filter algorithm. We illustrate on several challenging examples the benefits of this procedure for online approximate Bayesian parameter inference, and with one real data example we show that its online predictive performance can significantly outperform that of stochastic gradient descent and of streaming variational Bayes.