Online Approximate Bayesian learning
Paper and Code
Jul 15, 2020
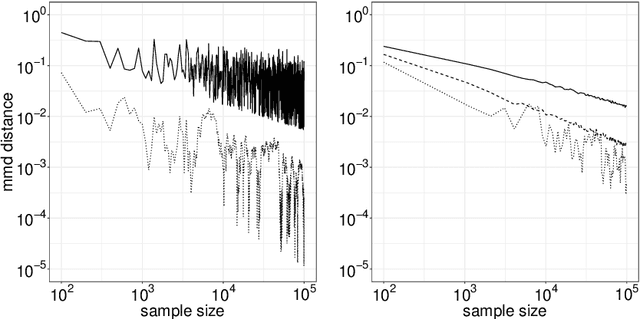
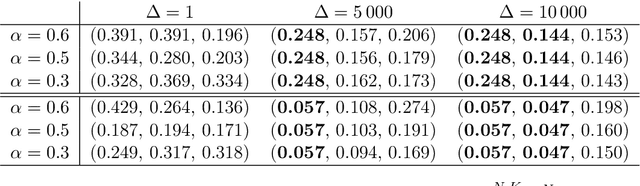
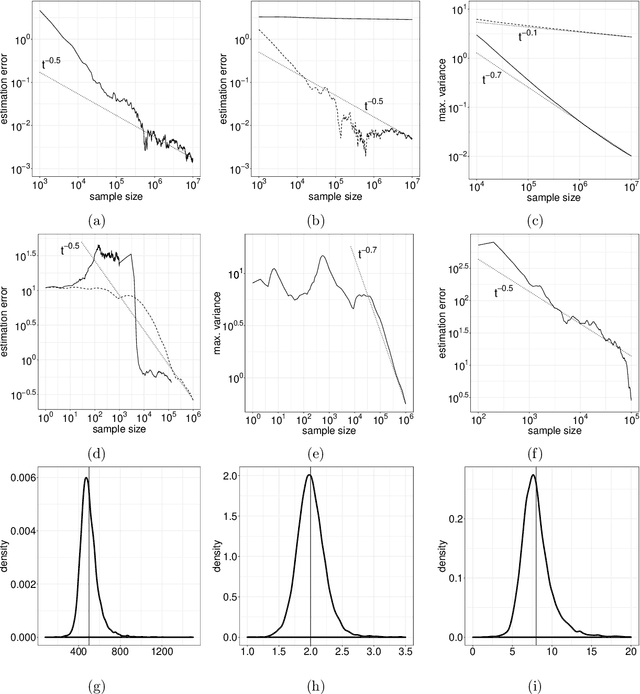
We introduce in this work a new method for online approximate Bayesian learning, whose main idea is to approximate the sequence $(\pi_t)_{t\geq 1}$ of posterior distributions by a sequence $(\tilde{\pi}_t)_{t\geq 1}$ which (i) can be estimated in an online fashion using sequential Monte Carlo methods and (ii) is shown to converge to the same distribution as the sequence $(\pi_t)_{t\geq 1}$, under weak assumptions on the statistical model at hand. In its simplest version, the proposed approach amounts to take for $(\tilde{\pi}_t)_{t\geq 1}$ the sequence of filtering distributions associated to a particular state-space model, and to approximate this sequence using a standard particle filter algorithm. We illustrate on several challenging examples the benefits of this procedure for online approximate Bayesian parameter inference, and with one real data example we show that its online predictive performance can significantly outperform that of stochastic gradient descent and of streaming variational Bayes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge