Monotonic Alpha-divergence Minimisation
Paper and Code
Mar 09, 2021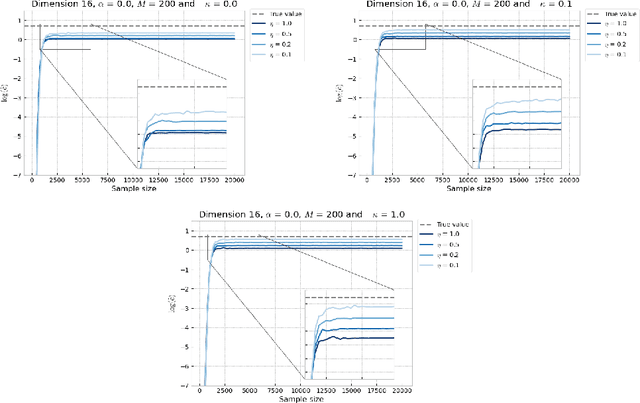
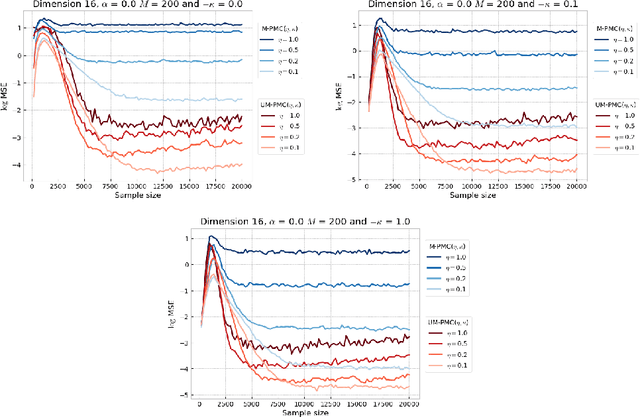
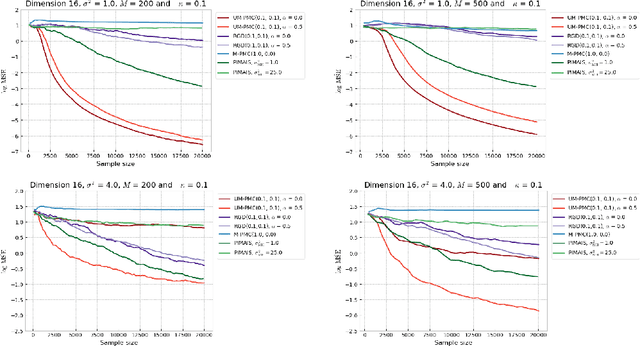

In this paper, we introduce a novel iterative algorithm which carries out $\alpha$-divergence minimisation by ensuring a systematic decrease in the $\alpha$-divergence at each step. In its most general form, our framework allows us to simultaneously optimise the weights and components parameters of a given mixture model. Notably, our approach permits to build on various methods previously proposed for $\alpha$-divergence minimisation such as gradient or power descent schemes. Furthermore, we shed a new light on an integrated Expectation Maximization algorithm. We provide empirical evidence that our methodology yields improved results, all the while illustrating the numerical benefits of having introduced some flexibility through the parameter $\alpha$ of the $\alpha$-divergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge