Learning with Importance Weighted Variational Inference: Asymptotics for Gradient Estimators of the VR-IWAE Bound

Several popular variational bounds involving importance weighting ideas have been proposed to generalize and improve on the Evidence Lower BOund (ELBO) in the context of maximum likelihood optimization, such as the Importance Weighted Auto-Encoder (IWAE) and the Variational R\'enyi (VR) bounds. The methodology to learn the parameters of interest using these bounds typically amounts to running gradient-based variational inference algorithms that incorporate the reparameterization trick. However, the way the choice of the variational bound impacts the outcome of variational inference algorithms can be unclear. Recently, the VR-IWAE bound was introduced as a variational bound that unifies the ELBO, IWAE and VR bounds methodologies. In this paper, we provide two analyses for the reparameterized and doubly-reparameterized gradient estimators of the VR-IWAE bound, which reveal the advantages and limitations of these gradient estimators while enabling us to compare of the ELBO, IWAE and VR bounds methodologies. Our work advances the understanding of importance weighted variational inference methods and we illustrate our theoretical findings empirically.

New penalized criteria for smooth non-negative tensor factorization with missing entries

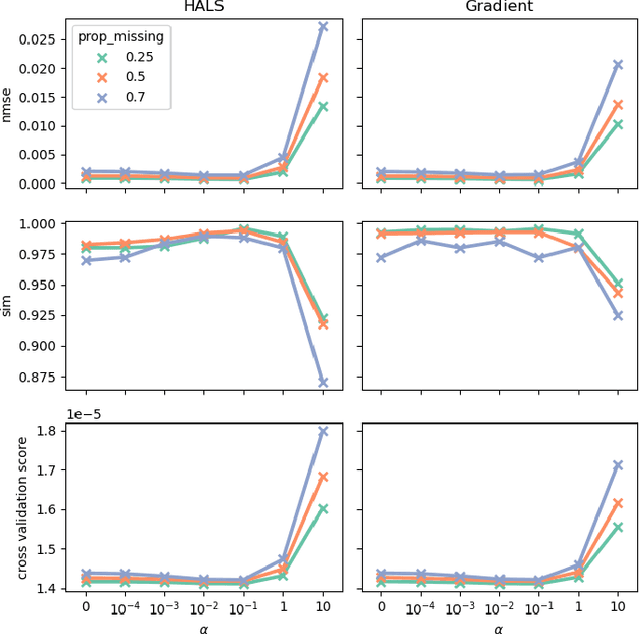
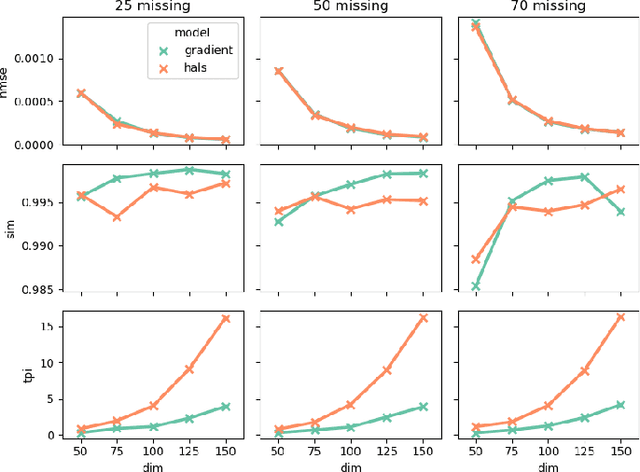
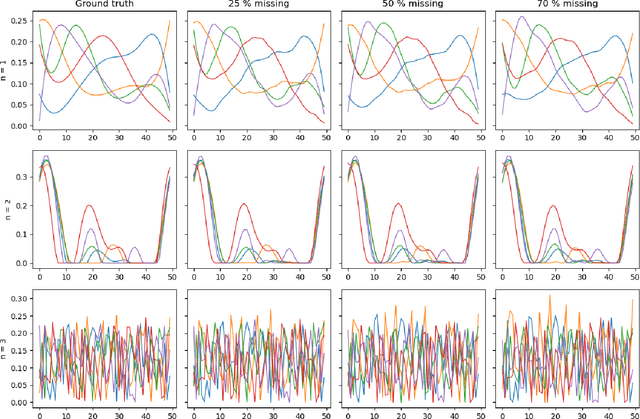
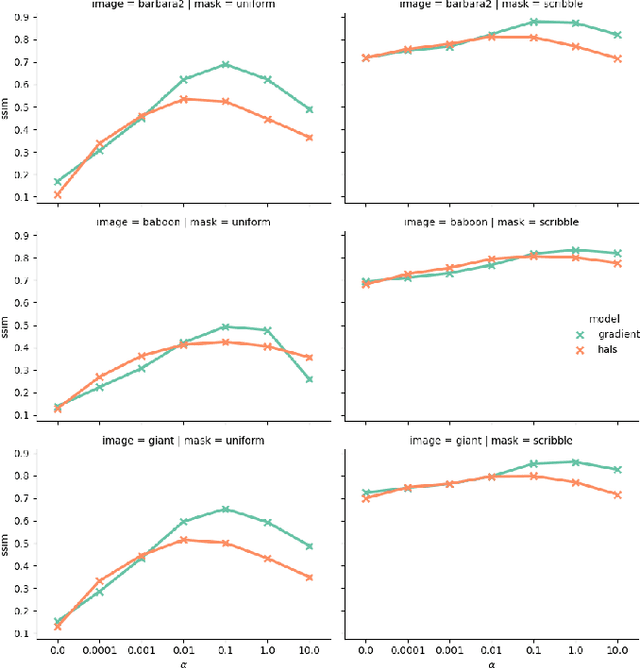
Tensor factorization models are widely used in many applied fields such as chemometrics, psychometrics, computer vision or communication networks. Real life data collection is often subject to errors, resulting in missing data. Here we focus in understanding how this issue should be dealt with for nonnegative tensor factorization. We investigate several criteria used for non-negative tensor factorization in the case where some entries are missing. In particular we show how smoothness penalties can compensate the presence of missing values in order to ensure the existence of an optimum. This lead us to propose new criteria with efficient numerical optimization algorithms. Numerical experiments are conducted to support our claims.

Smooth nonnegative tensor factorization for multi-sites electrical load monitoring

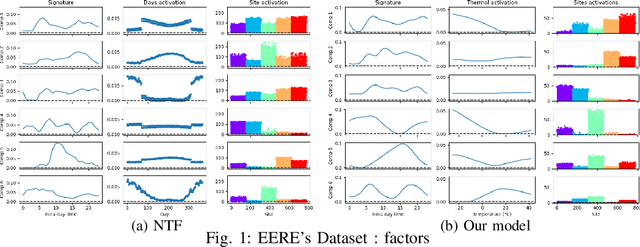
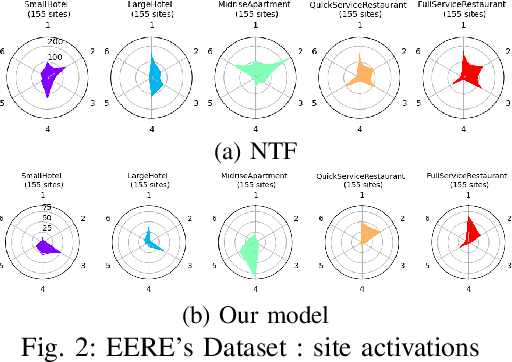
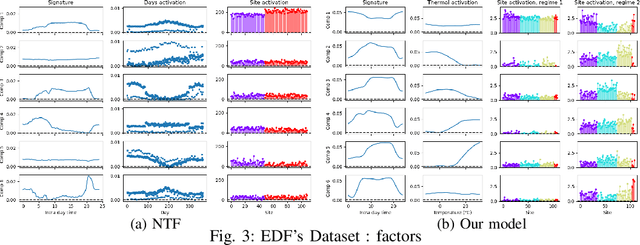
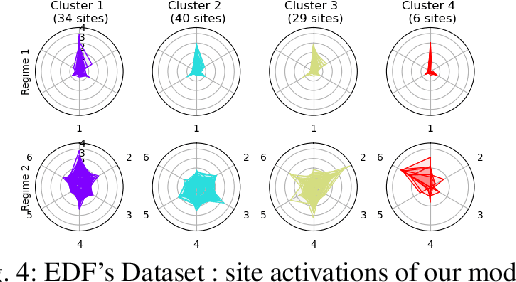
The analysis of load curves collected from smart meters is a key step for many energy management tasks ranging from consumption forecasting to customers characterization and load monitoring. In this contribution, we propose a model based on a functional formulation of nonnegative tensor factorization and derive updates for the corresponding optimization problem. We show on the concrete example of multi-sites load curves disaggregation how this formulation is helpful for 1) exhibiting smooth intraday consumption patterns and 2) taking into account external variables such as the outside temperature. The benefits are demonstrated on simulated and real data by exhibiting a meaningful clustering of the observed sites based on the obtained decomposition.

Monotonic Alpha-divergence Minimisation

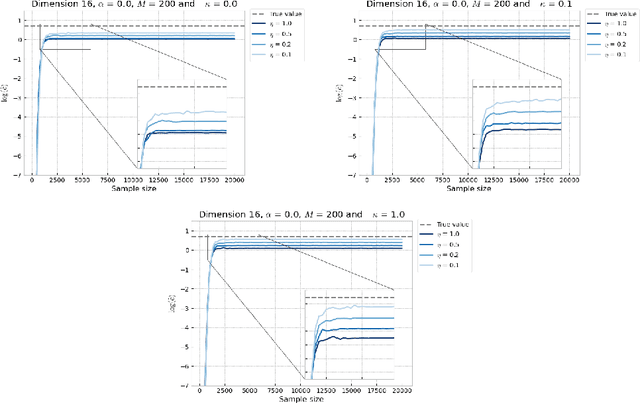
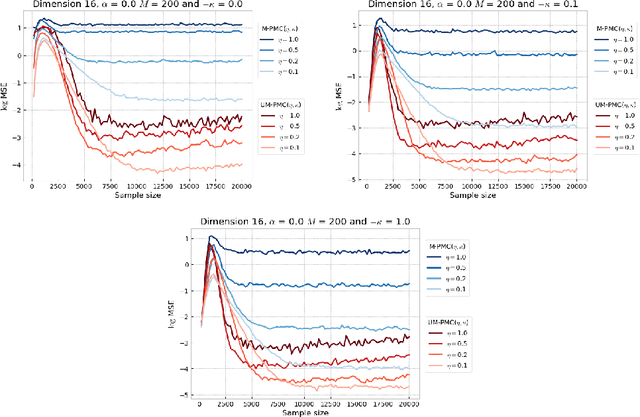
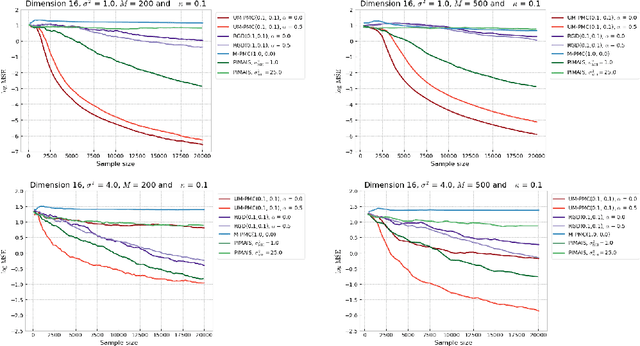
In this paper, we introduce a novel iterative algorithm which carries out $\alpha$-divergence minimisation by ensuring a systematic decrease in the $\alpha$-divergence at each step. In its most general form, our framework allows us to simultaneously optimise the weights and components parameters of a given mixture model. Notably, our approach permits to build on various methods previously proposed for $\alpha$-divergence minimisation such as gradient or power descent schemes. Furthermore, we shed a new light on an integrated Expectation Maximization algorithm. We provide empirical evidence that our methodology yields improved results, all the while illustrating the numerical benefits of having introduced some flexibility through the parameter $\alpha$ of the $\alpha$-divergence.

Nonlinear Functional Output Regression: a Dictionary Approach

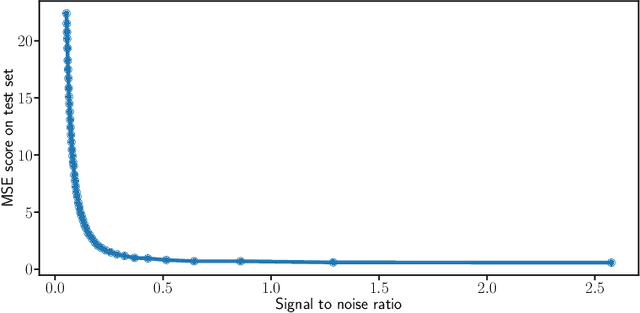
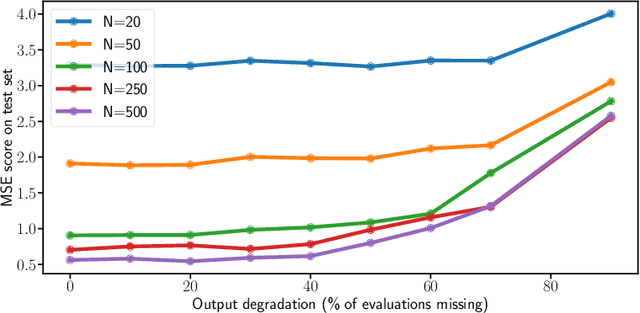
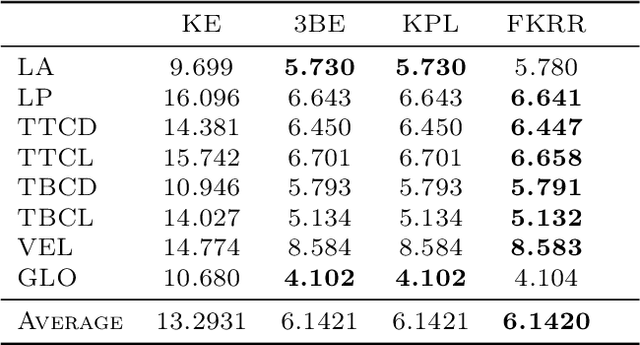
Many applications in signal processing involve data that consists in a high number of simultaneous or sequential measurements of the same phenomenon. Such data is inherently high dimensional, however it contains strong within observation correlations and smoothness patterns which can be exploited in the learning process. A relevant modelling is provided by functional data analysis. We consider the setting of functional output regression. We introduce Projection Learning, a novel dictionary-based approach that combines a representation of the functional output on this dictionary with the minimization of a functional loss. This general method is instantiated with vector-valued kernels, allowing to impose some structure on the model. We prove general theoretical results on projection learning, with in particular a bound on the estimation error. From the practical point of view, experiments on several data sets show the efficiency of the method. Notably, we provide evidence that Projection Learning is competitive compared to other nonlinear output functional regression methods and shows an interesting ability to deal with sparsely observed functions with missing data.

Anomaly Detection and Localisation using Mixed Graphical Models

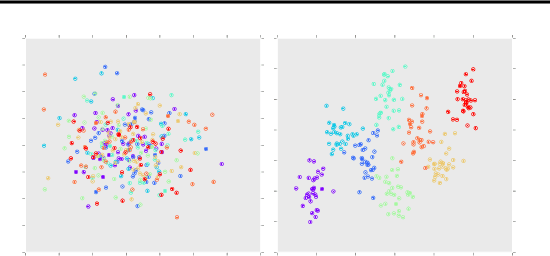
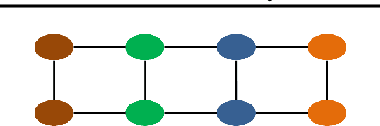
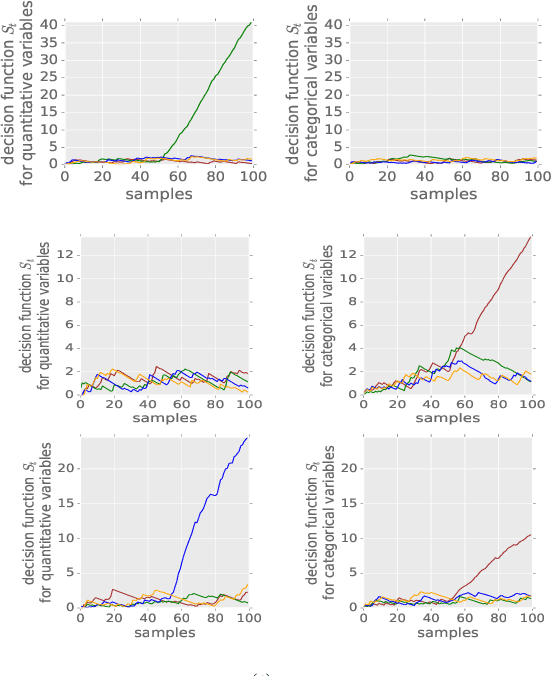
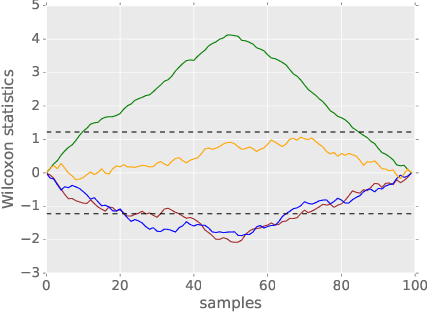
We propose a method that performs anomaly detection and localisation within heterogeneous data using a pairwise undirected mixed graphical model. The data are a mixture of categorical and quantitative variables, and the model is learned over a dataset that is supposed not to contain any anomaly. We then use the model over temporal data, potentially a data stream, using a version of the two-sided CUSUM algorithm. The proposed decision statistic is based on a conditional likelihood ratio computed for each variable given the others. Our results show that this function allows to detect anomalies variable by variable, and thus to localise the variables involved in the anomalies more precisely than univariate methods based on simple marginals.

Aggregation of predictors for nonstationary sub-linear processes and online adaptive forecasting of time varying autoregressive processes

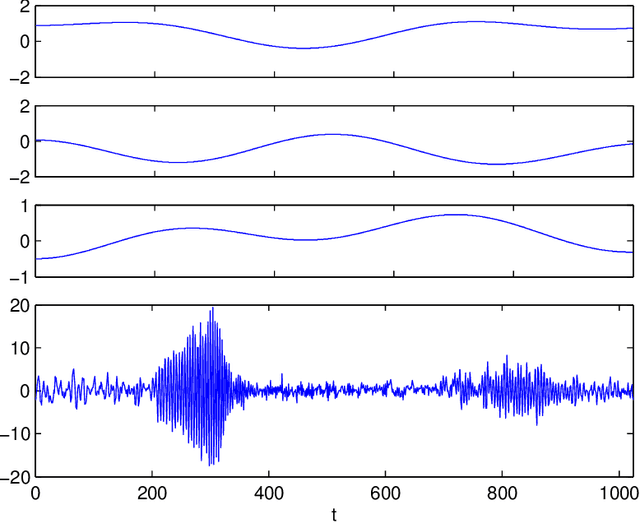
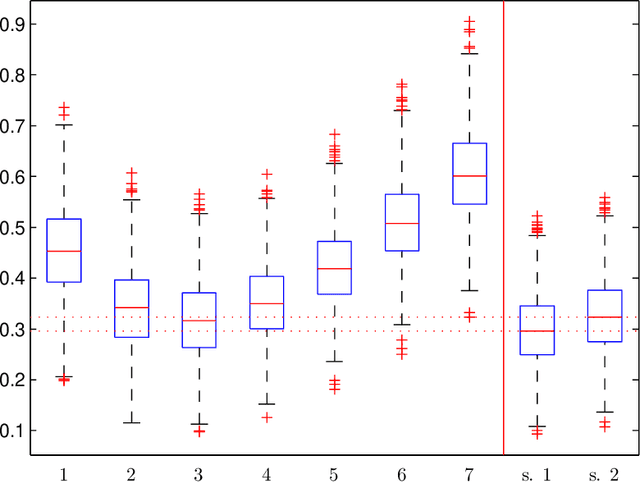
In this work, we study the problem of aggregating a finite number of predictors for nonstationary sub-linear processes. We provide oracle inequalities relying essentially on three ingredients: (1) a uniform bound of the $\ell^1$ norm of the time varying sub-linear coefficients, (2) a Lipschitz assumption on the predictors and (3) moment conditions on the noise appearing in the linear representation. Two kinds of aggregations are considered giving rise to different moment conditions on the noise and more or less sharp oracle inequalities. We apply this approach for deriving an adaptive predictor for locally stationary time varying autoregressive (TVAR) processes. It is obtained by aggregating a finite number of well chosen predictors, each of them enjoying an optimal minimax convergence rate under specific smoothness conditions on the TVAR coefficients. We show that the obtained aggregated predictor achieves a minimax rate while adapting to the unknown smoothness. To prove this result, a lower bound is established for the minimax rate of the prediction risk for the TVAR process. Numerical experiments complete this study. An important feature of this approach is that the aggregated predictor can be computed recursively and is thus applicable in an online prediction context.