Functional Output Regression with Infimal Convolution: Exploring the Huber and $ε$-insensitive Losses

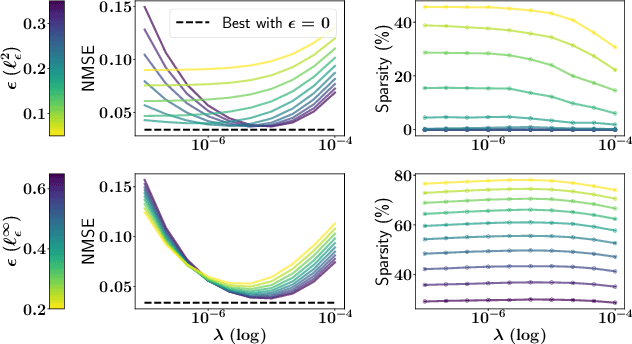
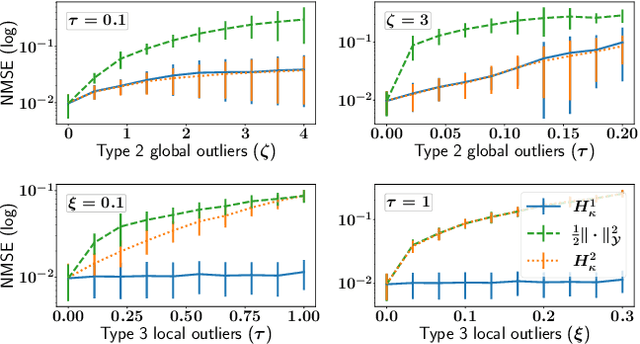
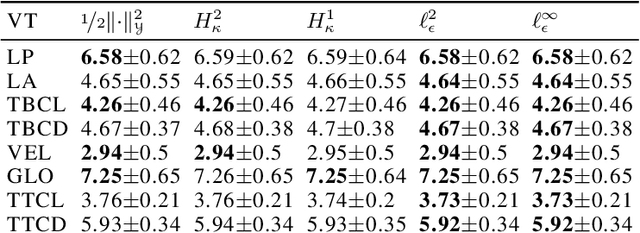
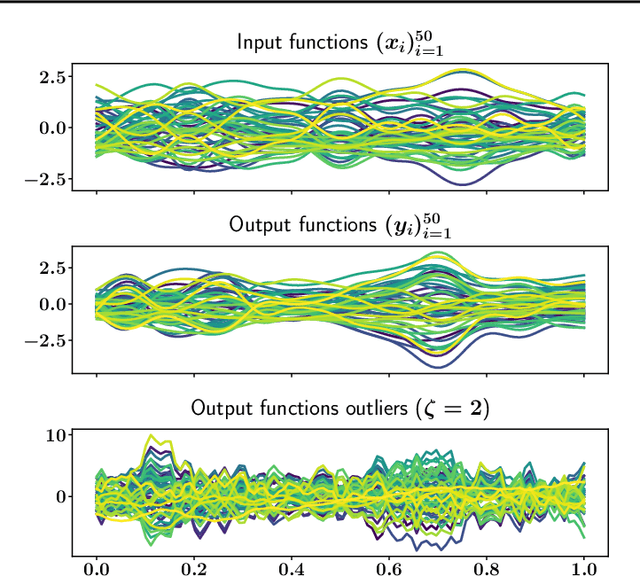
The focus of the paper is functional output regression (FOR) with convoluted losses. While most existing work consider the square loss setting, we leverage extensions of the Huber and the $\epsilon$-insensitive loss (induced by infimal convolution) and propose a flexible framework capable of handling various forms of outliers and sparsity in the FOR family. We derive computationally tractable algorithms relying on duality to tackle the resulting tasks in the context of vector-valued reproducing kernel Hilbert spaces. The efficiency of the approach is demonstrated and contrasted with the classical squared loss setting on both synthetic and real-world benchmarks.

Wind power predictions from nowcasts to 4-hour forecasts: a learning approach with variable selection

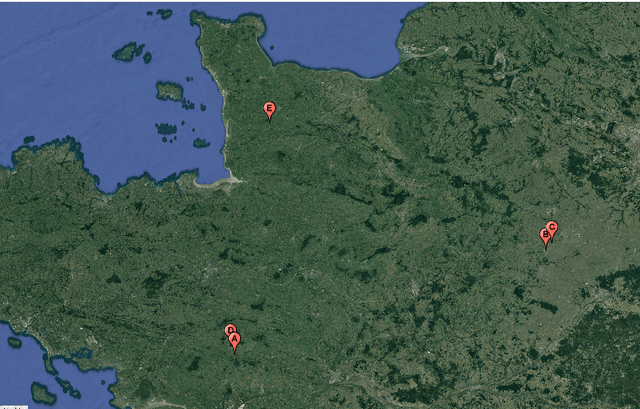
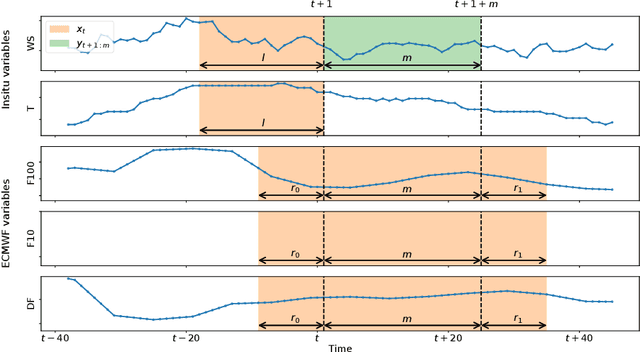
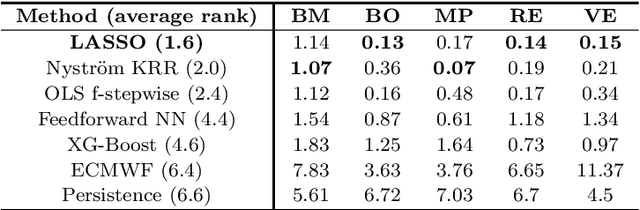
We study the prediction of short term wind speed and wind power (every 10 minutes up to 4 hours ahead). Accurate forecasts for those quantities are crucial to mitigate the negative effects of wind farms' intermittent production on energy systems and markets. For those time scales, outputs of numerical weather prediction models are usually overlooked even though they should provide valuable information on higher scales dynamics. In this work, we combine those outputs with local observations using machine learning. So as to make the results usable for practitioners, we focus on simple and well known methods which can handle a high volume of data. We study first variable selection through two simple techniques, a linear one and a nonlinear one. Then we exploit those results to forecast wind speed and wind power still with an emphasis on linear models versus nonlinear ones. For the wind power prediction, we also compare the indirect approach (wind speed predictions passed through a power curve) and the indirect one (directly predict wind power).

Nonlinear Functional Output Regression: a Dictionary Approach

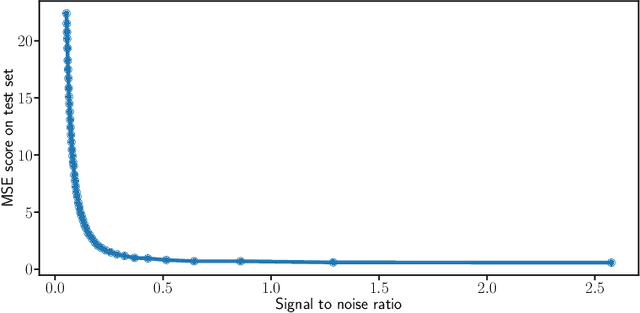
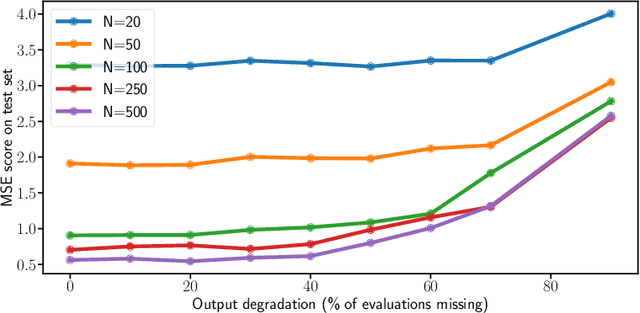
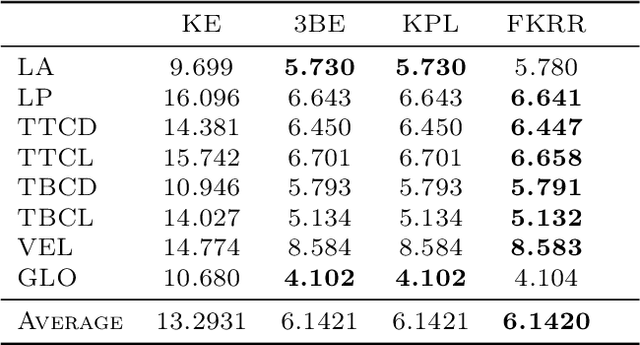
Many applications in signal processing involve data that consists in a high number of simultaneous or sequential measurements of the same phenomenon. Such data is inherently high dimensional, however it contains strong within observation correlations and smoothness patterns which can be exploited in the learning process. A relevant modelling is provided by functional data analysis. We consider the setting of functional output regression. We introduce Projection Learning, a novel dictionary-based approach that combines a representation of the functional output on this dictionary with the minimization of a functional loss. This general method is instantiated with vector-valued kernels, allowing to impose some structure on the model. We prove general theoretical results on projection learning, with in particular a bound on the estimation error. From the practical point of view, experiments on several data sets show the efficiency of the method. Notably, we provide evidence that Projection Learning is competitive compared to other nonlinear output functional regression methods and shows an interesting ability to deal with sparsely observed functions with missing data.