Functional Output Regression with Infimal Convolution: Exploring the Huber and $ε$-insensitive Losses
Paper and Code
Jun 16, 2022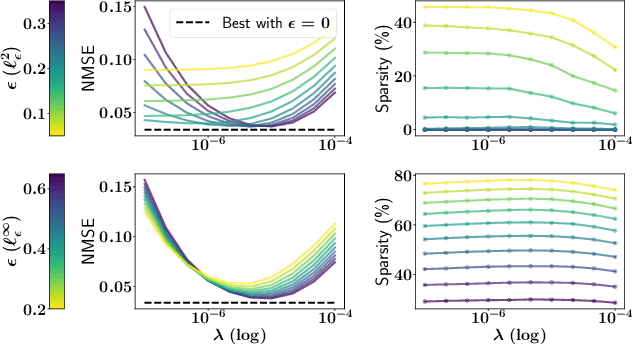
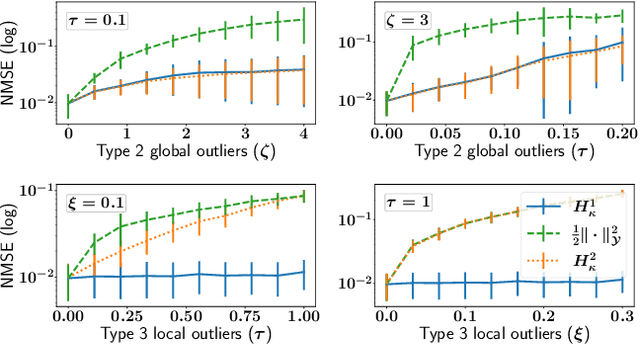
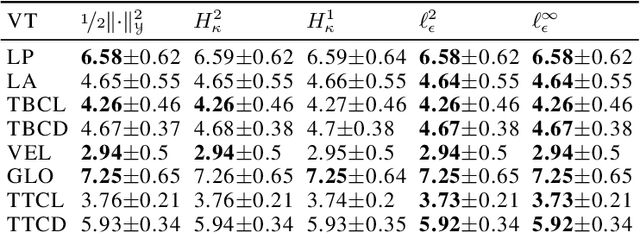
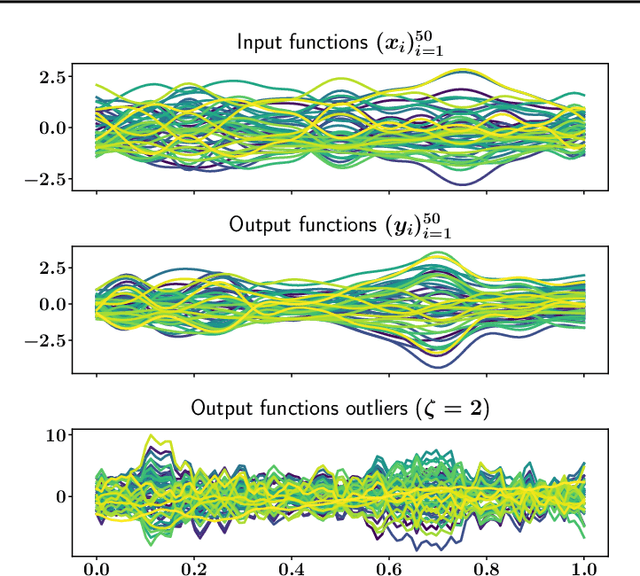
The focus of the paper is functional output regression (FOR) with convoluted losses. While most existing work consider the square loss setting, we leverage extensions of the Huber and the $\epsilon$-insensitive loss (induced by infimal convolution) and propose a flexible framework capable of handling various forms of outliers and sparsity in the FOR family. We derive computationally tractable algorithms relying on duality to tackle the resulting tasks in the context of vector-valued reproducing kernel Hilbert spaces. The efficiency of the approach is demonstrated and contrasted with the classical squared loss setting on both synthetic and real-world benchmarks.
* 24 pages, ICML 2022
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge