Nonlinear Functional Output Regression: a Dictionary Approach

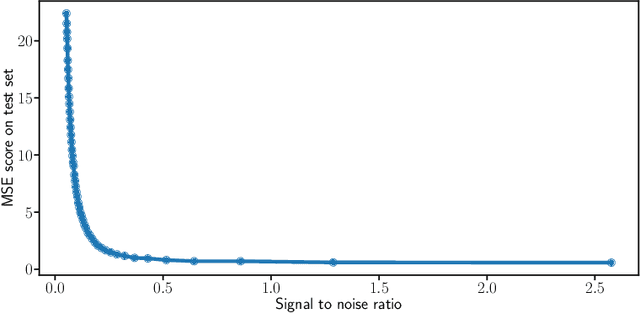
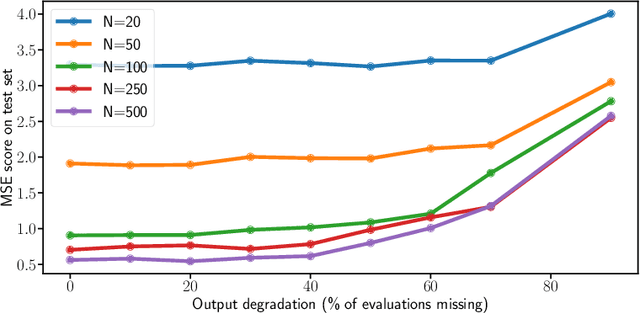
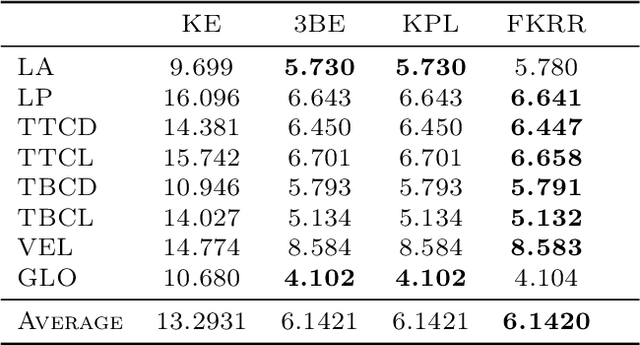
Many applications in signal processing involve data that consists in a high number of simultaneous or sequential measurements of the same phenomenon. Such data is inherently high dimensional, however it contains strong within observation correlations and smoothness patterns which can be exploited in the learning process. A relevant modelling is provided by functional data analysis. We consider the setting of functional output regression. We introduce Projection Learning, a novel dictionary-based approach that combines a representation of the functional output on this dictionary with the minimization of a functional loss. This general method is instantiated with vector-valued kernels, allowing to impose some structure on the model. We prove general theoretical results on projection learning, with in particular a bound on the estimation error. From the practical point of view, experiments on several data sets show the efficiency of the method. Notably, we provide evidence that Projection Learning is competitive compared to other nonlinear output functional regression methods and shows an interesting ability to deal with sparsely observed functions with missing data.