New penalized criteria for smooth non-negative tensor factorization with missing entries
Paper and Code
Mar 22, 2022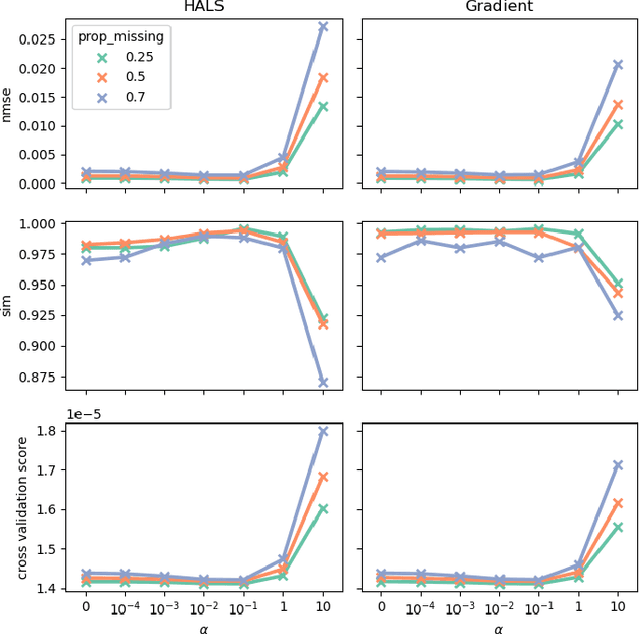
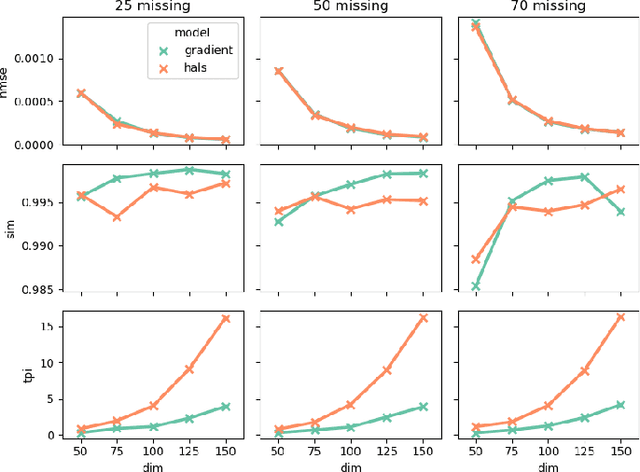
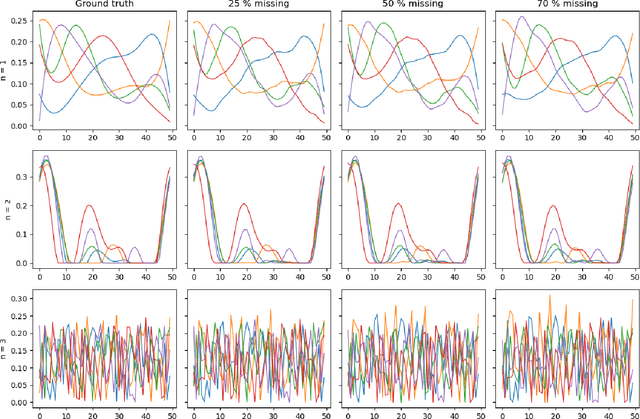
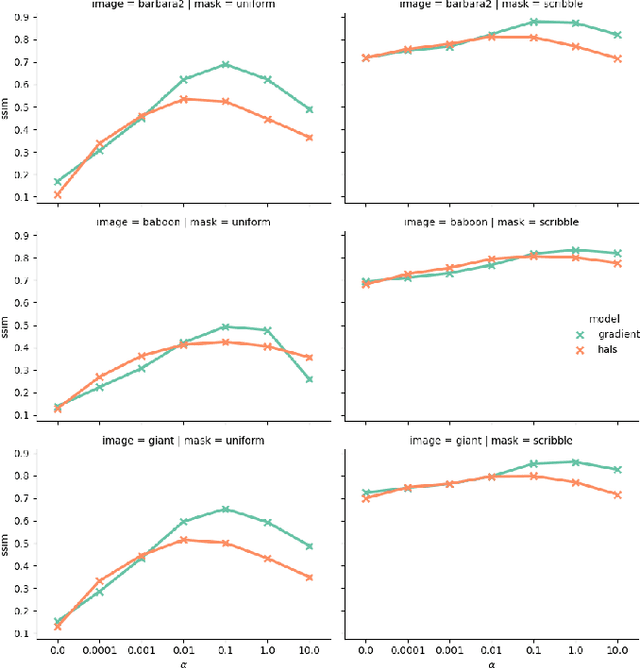
Tensor factorization models are widely used in many applied fields such as chemometrics, psychometrics, computer vision or communication networks. Real life data collection is often subject to errors, resulting in missing data. Here we focus in understanding how this issue should be dealt with for nonnegative tensor factorization. We investigate several criteria used for non-negative tensor factorization in the case where some entries are missing. In particular we show how smoothness penalties can compensate the presence of missing values in order to ensure the existence of an optimum. This lead us to propose new criteria with efficient numerical optimization algorithms. Numerical experiments are conducted to support our claims.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge